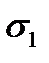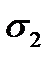Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос № 48. Начальная критическая нагрузка.Содержание книги
Поиск на нашем сайте
Начальная критическая нагрузка характеризует пределы применимости теории линейно-деформируемой среды. Если давление на грунт не превышает эту нагрузку, то ни в одной точке грунтового массива касательное напряжение не превосходит предельное. При превышении же этой нагрузки в грунте происходит формирование зон предельного состояния. Впервые задача об определении начальной критической нагрузки была решена Н.П. Пузыревским в 1929 г. Независимо от него подобное решение позже получил Н.М. Герсеванов.
Здесь
Структура формулы показывает, какая часть от общей нагрузки зависит соответственно от ширины штампа, глубины его заложения и сцепления грунта.
Вопрос № 49. Условия предельного состояния грунтов. Теория предельного состояния описывает поведение грунта под нагрузкой в третьей стадии деформирования (выпора). По этой теории рассматриваются вопросы, связанные с устойчивостью откосных сооружений, давлением на ограждающие конструкции, предельными нагрузками на грунт. Предельное напряженное состояние грунта соответствует такому напряженному состоянию, когда малейшее добавочное воздействие нарушает существующее равновесие и приводит грунт в неустойчивое состояние: в массиве грунта возникают поверхности скольжения, разрывы, просадки и нарушается прочность между его частями и их агрегатами. Для грунтового массива, загруженного внешней нагрузкой (плоская задача) известны компоненты напряжений
Ɵ R
Из сопротивления материалов известно, что значение Для сыпучих грунтов во всех случаях Для связных грунтов давление связности рассматривается как сила всестороннего сжатия, равная
Вопрос № 50. Предельные круги Мора. На кругах Мора можно установить, при каких значениях главных напряжений и их соотношениях между собой произойдет переход грунта в предельное состо-яние. Круги Мора рассматриваются в курсе «Сопротивление материалов». Исходными данными для построения кругов Мора служат компоненты главных напряжений

n
τ
σ
Если компоненты напряжений в точке увеличивать по абсолютной величине, не меняя их соотношение, то радиус кругов Мора будет также возрастать. Круг Мора, при котором грунт переходит в предельное состояние, называется предельным кругом Мора. Очевидно, что предельный круг Мора и зависимость Кулона должны иметь общую точку. Значит, зависимость Кулона должна быть касательной к предельным кругам Мора. Из построения круга Мора следует, что угол Ɵ есть отклонение полного напряжения от нормали к площадке. Очевидно, что максимально возможное отклонение этого угла равно углу внутреннего трения. Тогда первое условие перехода грунта в предельное состояние принимает вид: Ɵ=ᵠ.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.49.90 (0.006 с.) |


 - коэффициенты, зависящие от j, их значения табулированы и приведены в нормативных документах.
- коэффициенты, зависящие от j, их значения табулированы и приведены в нормативных документах. - удельные веса грунта ниже и выше подошвы.
- удельные веса грунта ниже и выше подошвы.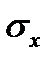 ,
,  , τ в произвольной точке и характеристики грунта: угол внутреннего трения и сцепление. Грунт может перейти в предельное состояние при определенном соотношении между известными характеристиками грунта.
, τ в произвольной точке и характеристики грунта: угол внутреннего трения и сцепление. Грунт может перейти в предельное состояние при определенном соотношении между известными характеристиками грунта. и
и  , а к площадке, отклоненной на угол α от главной площадки, по которой действует наибольшее главное напряжение, приложена равнодействующая R под углом Ɵ к нормали. Значение угла Ɵ при изменении угла α от 0 до 90٥ сначала возрастает от нуля до некоторого
, а к площадке, отклоненной на угол α от главной площадки, по которой действует наибольшее главное напряжение, приложена равнодействующая R под углом Ɵ к нормали. Значение угла Ɵ при изменении угла α от 0 до 90٥ сначала возрастает от нуля до некоторого  , а затем убывает до нуля.
, а затем убывает до нуля.


 может быть найдено из выражения:
может быть найдено из выражения:  .
. не может быть больше угла внутреннего трения ᵠ. Следовательно, условием предельного равновесия сыпучих грунтов будет:
не может быть больше угла внутреннего трения ᵠ. Следовательно, условием предельного равновесия сыпучих грунтов будет: 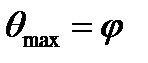 , или
, или  .
. . Прибавляя к
. Прибавляя к  и
и  по
по  , получим условие предельного равновесия связных грунтов:
, получим условие предельного равновесия связных грунтов:  или
или .
. и
и  .
.