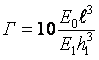Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурно-фазовая деформируемость грунтов.Содержание книги Поиск на нашем сайте
1. при передаче внешней нагрузки фазы грунта по-разному ведут себя; 2. при рассмотрении грунтов необходимо выделять связные структуры и сыпучие; 3. при нагружении в грунтах возникают упругие и остаточные деформации; 4. при давлениях 0,1-0,3 МПа зависимость между деформациями и напряжениями линейна.
С ростом внешнего давления можно представить, что разрушение модели вызовет в первую очередь действие касательного напряжения, так как прочность структурных связей меньше, чем прочность минеральных частиц. Эти касательные напряжения будут восприниматься силами структурного сцепления и трения. Силы трения зависят от величины нормальных напряжений. Разрушение модели будет сопровождаться сдвигом по некоторой поверхности, т.е. формированием поверхности скольжения.
Формирование поверхностей сдвига в грунте связано с перемещением частиц.
Сопротивление грунта сдвигу 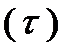 является основным показателем прочности грунта и используется при расчетах оснований и фундаментов. является основным показателем прочности грунта и используется при расчетах оснований и фундаментов.
Модель местных упругих деформаций. Модель упругого полупространства. Модель линейно-деформируемого слоя ограниченной толщины.
Метод угловых точек. Влияние формы и площади нагрузки.
12. Распределение напряжений под жестким штампом. Расчетное и фактическое впроцессе нагружения основания. Аналитическое решение по определению значений величин контактных напряжений, получено Буссинеску в виде зависимости:
Расчётная схема для решения задачи Буссинеску. Анализируя аналитическую зависимость (см. приведённую выше формулу и схему), можно записать, что При ρ = r → Рρ = ∞ При ρ = 0 → Рρ = 0,5Рср и построить теоретическую эпюру контактных напряжений. Фактически же, грунт под подошвой фундамента, при давлениях, стремящихся к бесконечности (краевые точки) разрушаясь, приводит к перераспределению напряжений, возникает практическая эпюра (см. приведенную схему). Однако в данной методике также не учитываются свойства грунта основания. При дальнейших исследованиях было установлено, что эпюра контактных напряжений под подошвой фундамента будет зависеть от его гибкости (Г) - обобщённой характеристики, учитывающей деформативные свойства основания. Р = f (Г) Понятие гибкости (Г) было введено профессором Горбуновым-Посадовым М.И.
Эпюры контактных напряжений под подошвой фундамента в зависимости от его гибкости. Крайняя правая схема на данном рисунке показывает, что для абсолютно жёстких фундаментов (Г=0), в целях аппроксимации, принята не фактическая седлообразная эпюра контактных напряжений, а прямоугольная (использование аппарата теории упругости к грунтам). Форма эпюры контактных напряжений зависит и от ширины подошвы фундамента Р = f(b) и при прочих равных условиях (mv – const; N – const) и может быть представлена на следующей схеме:
Эпюры контактных напряжений под подошвой фундамента в зависимости от его ширины. Форма эпюры контактных давлений зависит и от степени нагружения фундамента Р = f (N) и при прочих равных условиях (mv – const; F - const) может быть представлена на следующей схеме:
Эпюры контактных напряжений под подошвой фундамента в зависимости от степени нагружения. Таким образом, приведённые примеры дают наглядную картину изменения величины и формы эпюры контактных напряжений в зависимости от поэтапного нагружения (увеличение веса сооружения в процессе его строительства), что значительно осложняет решение поставленной задачи.
Распределение напряжений от собственного веса грунта. Расчетные случаи.
Общие положения теории ПНС. Фазы напряженного состояния,
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 936; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.17 (0.01 с.) |


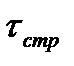
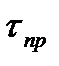

 - касательное напряжение, соответствующее структурным связям между частицами. Если
- касательное напряжение, соответствующее структурным связям между частицами. Если  , то грунт деформируется как сплошное тело. При
, то грунт деформируется как сплошное тело. При  >
>  частицы сдвигаются и
происходит более компактное их расположение.
частицы сдвигаются и
происходит более компактное их расположение.
 происходит формирование поверхностей скольжения
и разрушение грунта.
происходит формирование поверхностей скольжения
и разрушение грунта.






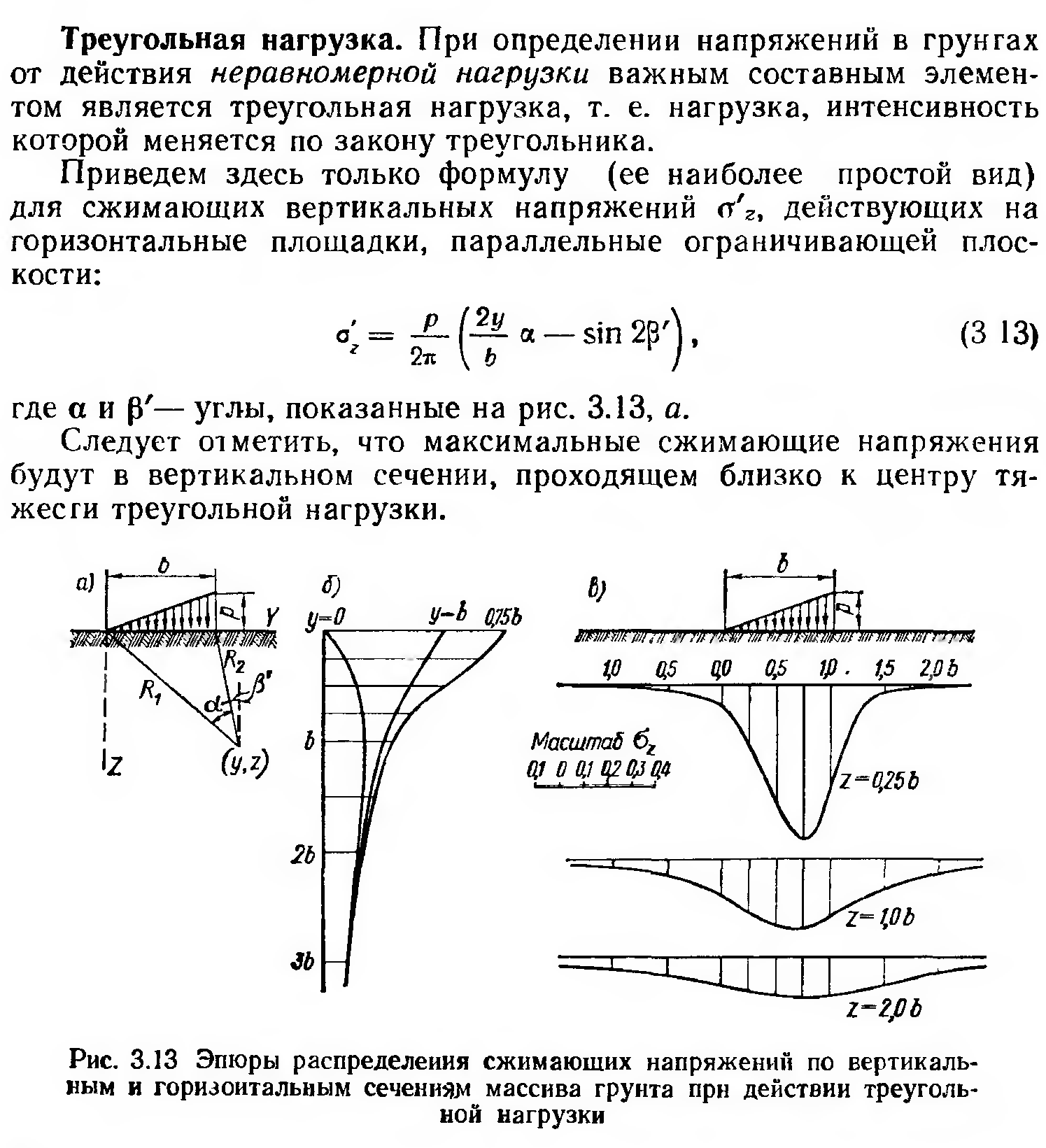
 11. Распределение напряжений в случае плоской задачи. Равномерная нагрузка. Нагрузка по треугольнику.
11. Распределение напряжений в случае плоской задачи. Равномерная нагрузка. Нагрузка по треугольнику.