
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Хар-ка напр-ий, действующий в зоне контакта частиц. Опр-е главных напр-ий в условиях плоской задачи.Содержание книги
Поиск на нашем сайте
Усл-я плоской задачи-напр-я распределяются в пл-ти чертежа, а в перпендикулярном направлении они =0 или имеют постоянное знач-е. Составляющие напр-ий в усл-ях плоской задачи: система σz=(P0/π)(α+sinαcos2δ); σy=(P0/π)(α – sinαcos2δ); τzy=τyz=(P0/π)sinαcos2δ. Переместим точку А в В, рас-ную на вертикальной оси при неизменной вертикальной координате. Знач-я углов для В: δ’= - α/2; δ=(α/2)-α/2=0. Т.о. если рассм-ая точка лежит на оси Z, то δ=0, cos0=1, sin0=0. Подставим в ф-лу для опр-я главных напр-ий получим: система σz=(P0/π)(α+sinα); σy=(P0/π)(α – sinα); Напр-я σz и σy будут хар-ться как главные взаимно перпендикулярные. Имея 2 вел-ны изобразить их можно графически через эллипс. Главные напр-я уменьшаются с увеличением глубины рассм. точки грунтового массива и по мере удаления от оси симметрии.
Вывод ф-лы Буссинеска через расчетную схему, постулат и усл-е равновесие.
P-(от 0 до π/2)ʃA(cosα/R2)cosα2π(Rsinα)(R d α)=0;
P-(от 0 до π/2)ʃA(cosα/R2)cosα2π(Rsinα)(R d α)=0; Проинтегрировав получим: Р-2/3Аπ=0; А=3/2*Р/π.подставив это выр-е в постулат получим: σR=(3*Рcosα)/(2πR^2)-ф-ла Буссинеска.
Опр-е напр-ий в усл-ях пространственной задачи.
Рассм-им гор-ую пл-ть кубика, на к-ой действует σz,τzy и τzx. Значение радиус-вектора σ’R можно опр-ть из подобного показателя σR: σ’R= σRcosα; cosα=z/R.
В рез-те получим вертикально нормальное напр-ние: σz=3Pz^3/2πR^5; Касательные напр-ния: τzy =3Pyz^2/2πR^5; τzx= 3Pxz^2/2πR^5 Учитывая, что R=√(z^2+r^2), получим: σz=КР/z^2. Постоянные члены выр-ния и координаты рассм. точки обозначим через коэф-т К Опр-е напр-ий под ленточным фундаментом и под трапецеидальной нагрузкой с помощью графика Остерберга. Ленточный фундамент: составляющие напр-ий в усл-ях плоской задачи опр-ся из ур-ний: система σz=KzP0; σy=KyP0; τyz,zy=Kyz, zyP0; где Кz, Ky, Kyz,zy –коэф-ты влияния, опр-ые по табл, в зависимости от знач-й относительных координат y/b; z/b, где y и z-абсолютные координаты точки грунтового массива, b-половина ширины. Мак-ые напр-я характерны для точек, расположенных на оси симметрии Z, следовательно σz>σy. Для глубины z<b норм-ые напр-я принимают постоянными: σz=P0, σy=0.6P0. Опр-е напр-ий в гр-те под нагрузкой, равномерно распределенной по ширине полосы: σz=(P0/π)(α+sinα)=K1P0, где К1-коэф-т влияния угла видимости, К1= (1/π)(α+sinα), где α-угол видимости, Р0-расчетное давление на гр-т от внешней нагрузки, Р0=Рс-0,01⍴h3, где Рс – давление сооружения, ⍴-пл-ть гр-а, h3 –вел-на заглубления фундамента. Значение К1 м.б. определено из соотношения 2b/z. Строят эпюру распределения напр-ий по глубине. Нагрузка по трапеции: норм-ое напр-е: σz=K2Р0; где К2-коэф-т, определяемый по графику Остерберга в зависимости от отношения a/z; b/z, где а-проекция линии откоса на горизонтальную пл-ть, b- половина ширины насыпи поверху, z- глубина опр-я напр-ия, Р0 - давление на грунт в центральной части насыпи, Р0=0,01⍴wН.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.197.120 (0.007 с.) |



 Действующие в гр-ах реальные силы, приложенные к отдельным грунтовым частицам, заменяют воображаемыми. Вел-у этих сил, отнесенных к ед-це площади сечения, принимают за вел-ну напр-ий в гр-те. Напр-я, действующие в зоне контакта двух частиц раскладываются на 2 составляющие:1. Норм-ое напр-е σ, действующее перпендикулярно к рассматриваемой площадке контакта; 2. Касат-ое напр-е τ, действующее в пл-ти площадки. Имея 2 составляющие можно получить результирующее-полное напр-е. Угол отклонения σп от нормальной вел-ны σ обозначим θ. Тогда: tgθ=τ/σ. Соотношение между норм-ым и кас-ым напр-ями хар-ся усл-ем равновесия.
Действующие в гр-ах реальные силы, приложенные к отдельным грунтовым частицам, заменяют воображаемыми. Вел-у этих сил, отнесенных к ед-це площади сечения, принимают за вел-ну напр-ий в гр-те. Напр-я, действующие в зоне контакта двух частиц раскладываются на 2 составляющие:1. Норм-ое напр-е σ, действующее перпендикулярно к рассматриваемой площадке контакта; 2. Касат-ое напр-е τ, действующее в пл-ти площадки. Имея 2 составляющие можно получить результирующее-полное напр-е. Угол отклонения σп от нормальной вел-ны σ обозначим θ. Тогда: tgθ=τ/σ. Соотношение между норм-ым и кас-ым напр-ями хар-ся усл-ем равновесия. τzy=τyz=0.
τzy=τyz=0. Если равномерно распределенную нагрузку заменить сосредоточенной силой, то напр-е в точках, равноудаленных от точки приложения силы, будут не равны между собой. Для опр-я σR примем постулат: напр-е σR пропорционально cosα и обратно пропорционально квадрату рас-ния от точки приложения сосредоточенной силы R2. σR=А(cosα/R2); где А- коэф-т, опр-ый из усл-я равновесия. Усл-е равновесия заключается в том, что сумма проекций всех сил на вертикальную ость= 0, т.е.: P-(от 0 до π/2)ʃσRcosα d F=0; d F- пов-ть элементарного шарового пояса, d F=2π(Rsinα)(R d α).Подставив эту вел-у в начальное ур-е, а также заменяя σR ф-лой, выраженной в постулате, получим:
Если равномерно распределенную нагрузку заменить сосредоточенной силой, то напр-е в точках, равноудаленных от точки приложения силы, будут не равны между собой. Для опр-я σR примем постулат: напр-е σR пропорционально cosα и обратно пропорционально квадрату рас-ния от точки приложения сосредоточенной силы R2. σR=А(cosα/R2); где А- коэф-т, опр-ый из усл-я равновесия. Усл-е равновесия заключается в том, что сумма проекций всех сил на вертикальную ость= 0, т.е.: P-(от 0 до π/2)ʃσRcosα d F=0; d F- пов-ть элементарного шарового пояса, d F=2π(Rsinα)(R d α).Подставив эту вел-у в начальное ур-е, а также заменяя σR ф-лой, выраженной в постулате, получим: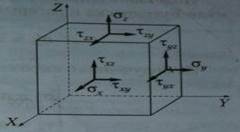 Пространственная задача хар-тся тремя взаимно перпендикулярными пл-тями XYZ. В связи с этим частицу гр-та рассм-им как элементарный кубик с равными пл-тями, на к-ые действуют соответствующие норм-е и кас-ые напр-я.
Пространственная задача хар-тся тремя взаимно перпендикулярными пл-тями XYZ. В связи с этим частицу гр-та рассм-им как элементарный кубик с равными пл-тями, на к-ые действуют соответствующие норм-е и кас-ые напр-я. Подставив σR по ф-ле Буссинеска и раскрыв cosα получим: σ’R=((3Рcosα)/(2πR^2)) z/R=3Pz^2/2πR^4.
Подставив σR по ф-ле Буссинеска и раскрыв cosα получим: σ’R=((3Рcosα)/(2πR^2)) z/R=3Pz^2/2πR^4. Из выражения опр-им напр-ия: σz= σ’Rcosα; cosα=Z/R; τzy= σ’Rcosβ; cosβ=Y/R; τzx= σ’Rcosγ; cosγ=X/R.
Из выражения опр-им напр-ия: σz= σ’Rcosα; cosα=Z/R; τzy= σ’Rcosβ; cosβ=Y/R; τzx= σ’Rcosγ; cosγ=X/R.


