
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные законы аэродинамикиСодержание книги
Поиск на нашем сайте
М1=М2=·····=Мn=const, Так как М=Q·ρ (здесь Q – объемный расход воздуха), то:
Но Q=υ·S (где ν – скорость движения воздуха, м/с; S – площадь поперечного сечения воздуховода, м2), следовательно (для двух сечений):
Уравнение (2.9.) называется уравнением неразрывности. Из него следует, что:
При ρ1=ρ2:
 , ,
т.е. скорость движения воздуха в различных поперечных сечениях воздуховода при ρ=const обратно пропорциональное площади его поперечного сечения. Из уравнения (2.8) при ρ1=ρ2:
а при ρ1≠ρ2:

Поправка на разность плотностей воздуха (ρ1/ρ2) достигает 8-10%. Закон сохранения энергии – энергия, поступающая в поток воздуха от внешних источников, полностью расходуется на преодоление всех сопротивлений на пути движения воздуха. Математической формулировкой закона сохранения энергии в рудничной аэрологии является уравнение Бернулли:
 , ,
где (р1-р2) – разность статических давлений воздуха в сечениях I и II (рис. 2.2.), Па; (g1Н1-g2Н2)– разность удельных давлений двух столбов воздуха, имеющих высоту Н1 и Н2 и удельный вес g1 и g2, Па; При решении инженерных вентиляционных задач коэффициенты к1 и к2 в уравнении (2.12.) можно принимать равными единице.
Разность (g1Н1-g2Н2) представляет собой так называемую естественную тягу. Эти члены вводятся в уравнение Бернулли, если первое сечение расположено на входе поступающей струи в воздуховод, а второе – на выходе из него. С учетом сказанного уравнение Бернулли может быть записано в упрощенном виде:
 , ,
или

Так как алгебраическая сумма статического и скоростного давлений Обозначив разность скоростных давлений через Dhск и депрессию естественной тяги через hе и приняв во внимание, что hе и Dhск могут быть как положительными, так и отрицательными, уравнение (2.12.) можно привести к виду:
Режимы движения воздуха и типы воздушных потоков Различают ламинарное и турбулентное движения воздуха. Ламинарное движение имеет место при малых скоростях движения воздуха, при этом воздушный поток состоит из несмешивающихся между собой параллельных слоев (струек). Турбулентное движение характеризуется беспорядочным изменением параметров течения воздуха во времени и пространстве и беспорядочным перемешиванием между слоями потока. При увеличении скорости движения воздуха ламинарное движение переходит в турбулентное.
Rе=νD/υ, где ν - средняя скорость движения воздуха, м/с; D – гидравлический диаметр воздуховода (выработки), м.
D=4S/P, где Sи Р – площадь поперечного сечения (м2) и периметр (м) воздуховода соответственно. В гладких трубах турбулентное движение имеет место при Re≥2300, а в подземных выработках – при Re≥1000-1500. Все воздушные потоки делятся на два типа: ограниченные потоки – потоки с твердыми границами и свободные потоки (или свободные струи) – потоки, не имеющие твердых границ.
Аэродинамическое сопротивление Закон сопротивления Закон сопротивления – зависимость между депрессией h и средней скоростью ν (или количеством Q) воздуха в воздуховоде (выработке). Теоретически и экспериментально установлено, что такая зависимость имеет параболический характер:
где С – постоянная, характеризующая текущую жидкость (газ, воздух), размеры и шероховатость трубопровода; х – показатель степени, зависящий от режима движения воздуха (при турбулентном движении х=2, при ламинарном х=1, при фильтрационном движении 2>х>1). Показатель х может быть определен экспериментально.
Виды сопротивлений Сопротивление трения. При движении воздуха в его потоке появляются силы трения под влиянием вязкости и эффекта прилипания. Т.к. стенки воздуховодов шероховаты, движущийся в них воздух оказывает давление на выступы шероховатости, т.е. появляется сила давления. Результатирующая сила называется силой трения, а вызываемое ею сопротивление – сопротивлением трения. В рудничной аэрологии выведена формула, связывающая количество проходящего по выработке воздуха (Q) с потерей напора (h), размерами и шероховатостью стен выработки:
 , ,
где α – коэффициент аэродинамического сопротивления трения, Н·с2/м4; L и Р – соответственно длина и периметр выработки, м; S – площадь поперечного сечения выработки, м2; Q – количество воздуха, м3/с. Для круглых труб:
 , ,
где D – диаметр трубопровода, м.
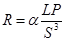 называется сопротивлением трения. называется сопротивлением трения.
Тогда, h=RQ2 Последнее уравнение является основным уравнением рудничной вентиляции. Оно дает возможность рассчитать величину депрессии, которую должен развить вентилятор, чтобы обеспечить заданный режим проветривания выработки (шахты) при известных α, L, P, S и Q. Величина α зависит от числа Рейнольдса Re (до 100000) и шероховатости стенок выработки, а также от площади поперечного сечения выработки. Значения α могут быть определены экспериментально в лаборатории или в натурных условиях. Имеются табулированные значения α для различных выработок [9]. В промышленной вентиляции потери давления на трение принято определять по выражению [7]:
 , н/м2 , н/м2
где λ – безразмерный коэффициент сопротивления трения; L и d – длина и диаметр воздуховода соответственно, м; ν – скорость движения воздуха, м/с; ρв – плотность воздуха, кг/м3. При установившемся турбулентном потоке коэффициент сопротивления трения может быть определен из выражения [7]:
 , ,
где rо – радиус трубы; ε – высота выступов шероховатости, мм. В ориентировочных расчетах можно принимать Местные сопротивления. К местным сопротивлениям относятся расширения, сужения, повороты, разветвления, вентиляционные окна. Потери давления (hм.с.) при проходе воздуха через местные сопротивления прямо пропорциональны скоростному напору воздуха, зависят от формы местного сопротивления и не зависят от его размеров:
 , ,
где ξ – безразмерный коэффициент местного сопротивления; ρв – плотность воздуха, кг/м3. Так как Q=νS, Величина где S – площадь поперечного сечения воздуховода, в котором скорость движения воздуха равна ν. Коэффициент ξ может быть определен экспериментально, подсчетом по эмпирическим формулам [1, 9]. Лобовое сопротивление. Лобовое сопротивление – сопротивление, оказываемое движущемуся воздуху находящимся в нем телом. Величина лобового сопротивления может быть определена по формуле:
 , ,
где С – коэффициент лобового сопротивления; Sm – миделево сечение тела, м2; S – площадь поперечного сечения воздуховода, м2. Коэффициент С зависит от числа Rе, формы и степени шероховатости поверхности тела.
Единицы сопротивления Из выражения h=RQ2:
Старая единица сопротивления -
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1866; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

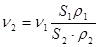
 ,
, - разность скоростных давлений в сечениях I и II, Па; ν1 и ν2 – средняя скорость движения воздуха в данных сечениях, м/с; к1 и к2 – коэффициенты кинетической энергии, учитывающие неравномерность распределения скоростей в сечениях I и II; h – разность давлений (депрессия), необходимая для преодоления сопротивления движению воздуха, Па.
- разность скоростных давлений в сечениях I и II, Па; ν1 и ν2 – средняя скорость движения воздуха в данных сечениях, м/с; к1 и к2 – коэффициенты кинетической энергии, учитывающие неравномерность распределения скоростей в сечениях I и II; h – разность давлений (депрессия), необходимая для преодоления сопротивления движению воздуха, Па. Разность давлений (р1-р2) создается работой вентилятора и называется депрессией вентилятора.
Разность давлений (р1-р2) создается работой вентилятора и называется депрессией вентилятора. есть полное давление, то на основании уравнения (2.14.) можно сказать, что на преодоление сопротивления движению воздуха по воздуховоду расходуется полное давление.
есть полное давление, то на основании уравнения (2.14.) можно сказать, что на преодоление сопротивления движению воздуха по воздуховоду расходуется полное давление. .
.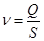 , то
, то  .
.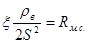 - местное сопротивление,
- местное сопротивление,
 , называемая киломюрг (кμ):
, называемая киломюрг (кμ):



