
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Та виконання лабораторних робітСодержание книги
Поиск на нашем сайте ТЕПЛОТЕХНІКА МЕТОДИЧНІ ВКАЗІВКИ До вивчення дисципліни Та виконання лабораторних робіт для студентів усіх спеціальностей денної та заочної форм навчання
Підписи авторів __________/Василенко С.М./ __________/Карась В.О./ __________/Сінат-Радченко Д.Є./ __________/Ткач Л.П./ __________/Агафонов В.П./ __________/Виноградов-Салтиков В.О./ __________/Маловічко В.С./ __________/Ямпольська І.М./ __________/ІващенкоН.В./ __________/Мельник З.П./ __________/Бондар В.І./
“ 01 “ вересня 2004 р. Підпис завідувача кафедри______________ “ 01 “ вересня 2004 р.
Київ НУХТ 2005 Теплотехніка: Метод. вказівки до вивч. дисципліни та викон. лаборатор. робіт для студ. усіх спец. ден. та заоч. форм навчання /Уклад.: С.М.Василенко, В.О.Карась, Д.Є.Сінат-Радченко, В.О.Виноградов-Салтиков та ін.– К.:НУХТ, 2005.─ 86с. Укладачі: С.М.Василенко, д-р техн.наук В.О.Карась, кандидат техн.наук Д.Є.Сінат-Радченко, кандидат техн.наук Л.П.Ткач, кандидат техн.наук В.О.Виноградов-Салтиков, кандидат техн.наук В.С.Маловічко, кандидат техн.наук В.П.Агафонов І.М.Ямпольська В.В.Іващенко З.П.Мельник, кандидат техн.наук В.І.Бондар Відповідальний за випуск Василенко С.М., д-р техн.наук
ОБРОБКА РЕЗУЛЬТАТІВ ВИМІРЮВАНЬ Вимірювання і види фізичних величин Одним із основних завдань проведення лабораторних робіт є визначення числових значень фізичних величин шляхом вимірювань. Вимірювання - це порівняння якоїсь фізичної величини з однорідною, взятою за одиницю (наприклад, розмір тіла порівнюється з одиницею довжини (1 м). Розрізняють прямі та непрямі вимірювання. У процесі прямих вимірювань значення фізичної величини визначають безпосередньо вимірюванням (час, маса, сила струму, довжина та ін.). Проте велика кількість фізичних величин (теплоємність, коефіцієнти теплопровідності, теплопередачі, конвективного теплообміну тощо) не може бути визначена безпосередньо вимірюванням. Їх обчислюють за певними рівняннями, до яких входять інші фізичні величини, що визначаються прямими вимірюваннями. Такі вимірювання називаються непрямими. У науці й техніці довільно встановлені лише деякі фізичні величини, які називаються основними. Решту одиниць фізичних величин встановлюють на основі математичних залежностей, які пов‘язують ці величини з основними. Такі одиниці називаються похідними. У Міжнародній системі одиниць СІ основними вживаються сім основних фізичних величин: довжина - метр [м], маса - кілограм [кг], час - секунда [с], термодинамічна температура - кельвін [К], сила електричного струму - ампер [А], сила світла - кандела [кд], кількість речовини - моль [моль]. Розрізняють істине і дійсне значення фізичної величини. Під істинним значенням фізичної величини розуміють ідеальне кількісне і якісне відображення властивостей даного об'єкта. Дійсне значення фізичної величини визначають експериментально з деякою похибкою.
Похибки прямих вимірювань Вимірювання фізичних величин - процес, що залежить від вимірюваної величини, точності використовуваної апаратури, методів вимірювання і, нарешті, від самого дослідника. Всі ці фактори спричиняють появу похибок вимірювань. Похибка вимірювання визначається як відхилення результату від його істинного значення. Різниця Da між істинним значенням a і величини за результатом вимірювання aвим. - називається абсолютною похибкою: Da = ½a - aвим.ô. Оскільки значення aневідоме, на практиці замість нього використовують експериментальне визначення значення `a, яке багаторазовим вимірюванням і обчисленням середньоарифметичного значення наближене до істинного. Ця різниця береться за модулем, оскільки відхилення результатів вимірювань може рівномірно відхилятися як у більший, так і у менший бік. Похибки поділяються на систематичні, випадкові й грубі (або промахи). Систематичні похибки пояснюються однією й тією самою постійною причиною (зміщення нуля шкали приладу, несправність приладу тощо). Систематичні похибки ще називають інструментальними. Найчастіше систематичні похибки усувають виправленням вимірювального приладу або обліком показів початкового зміщення стрілки приладу. Випадкові похибки спричинюються недосконалістю вимірювальних приладів і органів чуття людини, зміною зовнішніх умов тощо. Випадкові похибки усунути не можна. Якщо кількість вимірювань досить велика, випадкові похибки підпорядковуються закону ймовірності і їх можна обчислити. Грубі помилки (або промахи) виникають внаслідок неуважного відліку, несправності вимірювальних засобів, неправильного запису тощо. Такі вимірювання не розглядаються і відкидаються. У загальному випадку за n вимірювань величини a отримують an різних її значень. Найближчим до a є середньоарифметичне значення всіх результатів вимірювань æ n ö `a = (a1 +a2 + … + an)/n =ú ∑aiú /n. èi=1 ø Вводячи два знаки середньої абсолютної похибки D`a, встановлюють межі, в яких перебуває істинне значення шуканої величини: `a - D`a ≤ a - D`a. Чим менше значення D`a, тим менший інтервал, у якому міститься істинне значення вимірюваної величини, а отже, тим вища точність виміряної величини a. Абсолютну похибку вимірювань прирівнюють до власної похибки приладу за одноразового вимірювання або якщо в результаті вимірювань отримано ряд цілком однакових значень. Під відносною похибкою вимірюваної величини розуміють відношення значення абсолютної похибки вимірювання Da, до середньоарифметичного значення `a, %: Da e = ± ¾¾ 100. `a Відносна похибка дає уявлення про якість вимірювань: чим менша відносна похибка, тим точніше виміряна шукана величина. Якщо шукана величина a не може бути визначена за заданим рівнянням, у яке входять фізичні величини, отримані прямим вимірюванням, похибка залежить від похибок окремих прямих вимірювань. У процесі непрямих вимірювань Da обчислюється за похідною від заданого рівняння. Розглянемо кілька прикладів. Приклад 1. Шукана величина aдорівнює сумі двох величин В і С, що визначаються прямим вимірюванням: a= В + С. Нехай величина В визначена з точністю ±DВ, а С - з точністю ±DС. Тоді a= ±a= (В ±DВ) + (С±DС), звідки Da = ± (DВ + DС). Візьмемо найбільш невигідний випадок, коли знаки абсолютних похибок однакові. Така помилка називається межовою, або максимальною. Відносна похибка Da DВ+DС e= ¾¾ 100 = ¾¾¾ 100, %. a В + С Приклад 2. Шукана величина дорівнює добутку (частці) двох величин: a= В·С. Тоді a= ±a= (В ±DВ)·(С±DС)= В·С ± В·DС ± DВ·С ± DВ·DС. Добуток DВ·DС відкидаємо як величину другого порядку мализни. Тоді абсолютна похибка Da = ± (В·DС + DВ·С). Відносна похибка вимірю-вання Da В·DС + С·DВ æ DС DВ ö e= ¾¾ 100% =¾¾¾¾¾¾ 100 % = ç¾¾ - ¾¾÷ 100 %. a В·С è С В ø
Лабораторна робота 1
ВИМІРЮВАННЯ ТЕПЛОЄМНОСТІ ПОВІТРЯ Мета роботи: поглибити знання з теорії теплоємності; ознайомитися з експериментальним методом вимірювання теплоємності газів; дослідним шляхом визначити середню теплоємність повітря в інтервалі температур від 20 до 120 °С. Послідовність виконання роботи 1. Ознайомитися з експериментальною установкою, знайти всі основні елементи схеми. 2. Увімкнути вентилятор 10 і за допомогою автотрансформатора встановити за реометром заданий викладачем перепад тиску. 3. Увімкнути нагрівник 5 і за допомогою автотрансформатора 8 встановити задану потужність нагріву. 4. Виміряти та записати у табл.1.1 покази барометра 6. 5. Дочекатись встановлення стаціонарного режиму, що характеризується постійністю показів автоматичного потенціометра 12. 6. Зняти покази реометра V, ваттметра W, термометра t1, потенціометра t2 та занести їх у табл.1.1. 7. Аналогічно провести досліди для інших заданих режимів. 8. Після закінчення роботи вимкнути електронагрівник 5, вентилятор 10 та автоматичний потенціометр 12. Опрацювання результатів вимірювань. Експериментальні дані занести у табл.1.1, результати розрахунків - у табл.1.2 і 1.3. Таблиця 1.1
Таблиця 1.2
Таблиця 1.3
1. Об¢ємну витрату повітря, знайдену за показами реометра, звести до нормальних умов: Vн = Vрб×Тн / (рн× Т1), де Т1 = t1 + 273 – абсолютна температура повітря, К, на вході до калориметра. 2. Середня об¢ємна теплоємність повітря за постійного тиску ` ср = Q /[Vн(t2 - t1)], де Q=W – тепловий потік, що підводиться до повітря від електронагрівника (втратами теплоти в оточуюче середовище нехтують), Вт; t1, t2 – температура повітря відповідно на виході з калориметра та на вході в нього, °С. 3. Середня масова теплоємність повітря за постійного тиску `ср=`с′р ·V0 /m, де V0 = 22,4 м/кмоль - об¢єм 1 кмоль ідеального газу за нормальних умов; m= 29 кг/кмоль – маса 1 кмоль повітря. 4. Середня молярна теплоємність за постійного тиску `сmр = `ср· m. 5. Середня молярна теплоємність за постійного об¢єму ` сmυ= `сmр - Rm. 6. Середня масова теплоємність за постійного об¢єму `сυ= `сmυ/m. 7. Середня об¢ємна теплоємність за постійного об¢єму `сυ= `сmυ/V0. 8. Показник адіабати k=`cр/`сυ=`сmр/`сmυ. 9. Середня температура повітря в процесі нагрівання ` t= (t1 – t2 )/2. 10. У інтервалі температур від 0...120 °С теплоємність повітря δ`ср=(`ср - стр) 100 % / стр. 11.Розрахункова відносна похибка вимірювань: ε = (DW/W + DV/V + Dt/t)·100 %, де DW, DV, Dt– граничні абсолютні похибки вимірювань відповідно потужності, витрати повітря та температури. Для реометра DVвизначається ціною половини поділки шкали. Для потенціометра та ваттметра, крім ціни поділки шкали, слід ураховувати клас точності приладу. Розглянемо приклад визначення абсолютної похибки ватметра класа точності 0,5 (шкала 0...100 поділок) за умови, що струмова обмотка приладу увімкнена на I = 1А, а обмотка напруги на U = 100 В. Потужність, що відповідає максимальній поділці шкали ватметра W=UI = 100×1=100 Вт. Гранична абсолютна похибка приладу 100×0,005 = 0,5 Вт. Величина цієї похибки не залежить від того, на якій ділянці шкали проводиться вимірювання. Контрольний приклад Вхідні дані: рб = 100 кПа; t1 = 20 °С; t2 = 60 °С; V = 2,1×10-4 м3/с; W =10 Вт. Результати обчислень: 1. Vн =1,931﹒10-4 м/с. 2. 3. 4. 5. 6. 7. 8. k = 1,402. 9. ` t = 40 °С. 10. δср = 0,60 % 11. ε = 10 %. Контрольні запитання 1. Що таке теплоємність? 2. Перелічити види й характеристики питомих теплоємностей. 3. Зв¢язок між питомими масовою та об¢ємною, а також молярною 4. Як звести об¢єм газу до нормальних умов? 5. Написати й пояснити рівняння першого закону термодинаміки. 6. Написати та пояснити рівняння Майєра. Зміст універсальної та питомої газових сталих. 7. Який зв¢язок між об¢ємними теплоємностями за постійних тиску та об¢єму. 8. Як залежить теплоємність ідеального газу від числа атомів у 9. У який послідовності проводиться експеримент? 10. Що таке сталий тепловий режим? 11.Чи враховуються в даній роботі втрати теплоти в оточуюче 12. Які чинники впливають на точність визначення теплоємності? 13. Що таке показник адіабати і від чого він залежить? 14.Середня й істинна теплоємності. Зв¢язок між ними. 15.Як знайти середню теплоємність газу у заданому інтервалі температур? Лабораторна робота 2 Лабораторна робота 3 ДОСЛІДЖЕННЯ ЦИКЛУ ПАРОКОМПРЕСОРНОЇ ХОЛОДИЛЬНОЇ УСТАНОВКИ. Мета роботи: поглибити знання та набути практичних навичок з дослідження термодинамічних циклів одержання холоду, теоретичною основою яких є зворотний цикл Карно; ознайомитися з методикою визначення параметрів холодильного агента в характерних точках циклу за допомогою діаграм і розрахунку енергетичних показників холодильної установки. Діаграма lg p–h Для практичних розрахунків енергетичних характеристик циклів ПКХУ доцільно користуватись ентальпійними діаграмами, в яких легко будувати цикл та визначати ентальпії в характерних точках. На рис.3.3 зображено схему діаграми lg p–h, у якій на осі абсцис відкладено значення ентальпії в кДж/кг, а вісь ординат логарифмічна і на ній відкладено значення тиску в МПа. На цій діаграмі нанесено граничну криву, утворену лівою (х = 0) і правою (х = 1) гілкою. Точки на лівій гілці характеризують стан рідкого холодоагенту за температури насичення, на правій – сухої насиченої пари. Під граничною кривою речовина перебуває у двофазному стані і називається вологою насиченою парою. Праворуч від кривої х=1 – ділянка перегрітої пари (температура пари вища за температуру насичення). На діаграмі показані лінії сталої температури t = const (ізотерми), які на ділянці вологої начиченої пари збігаються з ізобарами р=const, лінії сталого об’єму υ=const, сталої ентропії s=const і лінії однакової міри сухості х = const.
Рис. 3.3 Порядок виконання роботи 1. Ознайомитися з основними елементами парокомпресорної холодильної установки. 2. Увімкнути цифровий вольтметр. 3. Дочекатися моменту увімкнення компресора (початку здійснення циклу) та розпочати вимірювання ЕРС термопар, почерговим з’єднанням їх з вольтметром за допомогою перемикача (проміжок між циклами вимірювань - близько однієї хвилини). 4. Останнє вимірювання провести після вимкнення компресора за 3 – 5 секунд. 5. За допомогою термометра, розміщеного в приміщенні лабораторії, визначити температуру навколишнього середовища (повітря). Опрацювання дослідних даних 1. Обчислити середні значення ЕРС кожної термопари в трьох останніх циклах вимірювання (у разі потреби порадитися з викладачем). 2. За допомогою градуювальної таблиці 3.1 знайти поправку, що враховує температуру допоміжного спаю термопари (ЕРС термопари за температури навколишнього середовища), додати її до середніх значень ЕРС з урахуванням знаку (алгебраїчна сума), занести до табл.3.1 для відповідних точок циклу.
Таблиця 3.1
3. Визначити температуру холодоагенту у характерних точках циклу за значеннями ЕРС термопар, використовуючи градуювальну таблицю. У зв’язку з тим що процеси 5–1 та 3–4 ізобарно-ізотермічні, t5=t1, а t3=t4. 4. Побудувати цикл ПКХУ на діаграмі lg p–h. Схему побудови циклу показано на рис.3.5. Приймається, що на виході з конденсатора рідкий холодоагент перебуває в стані насичення, а з випарника виходить суха насичена пара. Точка 4 знаходиться на перетині лівої гілки граничної кривої (х=0) та ізотерми t4 , точка 1 – на перетині правої гілки граничної кривої (х=1) та ізотерми t1. Через точки 4 і 1 провести олівцем тонкі горизонтальні лінії, які є відповідними ізобарами холодоагенту в конденсаторі та випарнику (р1, р2). Точка 5 знаходиться на перетині вертикальної лінії (h=const), проведеної з точки 4, і ізобари р2, точка 2 на перетині ізобари р1 та ізотерми t2, точка 3 – на перетині ізобари р1 і лінії х= 1. 5. За допомогою діаграми визначити параметри холодоагенту у всіх точках і занести їх до табл. 3.2. 6. Обчислити питому холодопродуктивність холодильної установки. 7. Визначити кількість теплоти, що передається до навколишнього середовища.
Рис. 3.5 8. Обчислити питому роботу, що витрачається на здійснення цикла. 9. За формулою (3.2) підрахувати значення холодильного коефіцієнта. 10. У протоколі лабораторної роботи накреслити (без масштабу) цикл ПКХУ в діаграмі lg p–h. Таблиця 3.2
Контрольні запитання. 1. Яка будова та принцип дії парокомпресорної холодильної установки? 2. Схема лабораторної установки, рух і зміна стану холодоагенту. 3. Цикл ПКХУ в координатах T–s. 4. Як зображується цикл ПКХУ в координатах lg p–h? 5. Яка послідовність проведення досліду, отримання дослідних даних? 6. Яка послідовність побудови циклу в координатах lg p–h. 7. Визначення та фізичний сенс питомої холодовидатності, її зв’язок з потужністю холодильної установки. 8. Як обчислити теплоту, що відводиться до навколишньго середовища, тепловий баланс ПКХУ. 9. Робота циклу, її обчислення та фактори, що впливають на величину роботи. 10. Обчислення та фізичний сенс холодильного коефіцієнта, його зв’язок з енергетичною ефективністю циклу ПКХУ. Лабораторна робота 4 Конвективна тепловіддача За законом Ньютона-Ріхмана конвективний тепловий потік, Вт, Qк = aкF(tc – tт), де aк – коефіцієнт конвективної тепловіддачі, Вт/(м2×К). Коефіцієнт конвективної тепловіддачі характеризує інтенсивність тепловіддачі і показує кількість теплоти, що передається між стінкою і теплоносієм за одиницю часу через одиницю площі поверхні цієї стінки, при температурному напорі 1 К. Конвективна тепловіддача – це складний процес, і коефіцієнт конвективної тепловіддачі aк залежить від багатьох факторів: роду теплоносія, його фізичних властивостей, швидкості руху, температури теплоносія та стінки, форми та розмірів поверхні теплообміну, виду та режиму руху теплоносія та ін. Фізичні властивості теплоносія, в свою чергу, залежать від температури. За природою виникнення існують два види руху: вільний (природний) та вимушений. Вільним називається рух, який виникає внаслідок різниці густин нагрітих і холодних частинок рідини чи газу. Інтенсивність вільного руху залежить, головним чином, від різниці температур. Вимушеним називають рух, що виникає внаслідок дії будь-яких збудників (насос, вентилятор, вітер). Інтенсивність вимушеного руху залежить від швидкості руху, фізичних властивостей середовища, форми та розмірів каналу. У процесі конвективної тепловіддачі вимушений рух може супроводжуватися вільним. Вплив останнього на інтенсивність тепловіддачі тим більший, чим більша різниця температур та чим менша швидкість вимушеного руху. На інтенсивність конвективної тепловіддачі суттєво впливає характер руху частинок біля поверхні теплообміну. За характером руху частинок розрізняють ламінарний і турбулентний режими руху. За ламінарного режиму частинки рідини чи газу рухаються упорядковано, паралельно до стінок каналу та траєкторій інших частинок. За турбулентного режиму частинки рухаються хаотично, напрямок і величина швидкості окремих частинок безперервно змінюються. Режим руху визначають за критеріями (числами) подібності. Критерії подібності – це безрозмірні комплекси фізичних величин, що характеризують той чи інший процес. Критерії подібності називають іменами видатних вчених і позначають першими двома латинськими літерами їх прізвищ. Режим вимушеного руху визначають за критерієм Рейнольдса, який характеризує інтенсивність руху і виражає співвідношення між інерційними силами у потоці і силами міжмолекулярного тертя
де w – середня швидкість руху теплоносія у каналі, м/с; n - кінематичний коефіцієнт в’язкості, м2/с; ℓ – визначальний лінійний розмір каналу, м; для круглих труб приймають ℓ = d (d – внутрішній діаметр труби); для не круглих – ℓ = dекв= 4f/П (dекв – еквівалентний діаметр каналу, м; f – площа поперечного перерізу каналу, м2; П – повний периметр каналу, м). За Re< 2×103 – режим руху ламінарний, за Re>1×104 - турбулентний, за 2×103<Re<1×104 – перехідний. Режим вільного руху визначають за критерієм Релея, що являє собою добуток критеріїв Грасгофа і Прандтля Ra = Gr×Pr. (4.2) Критерій Грасгофа Gr характеризує інтенсивність вільного руху і виражає співвідношення між підіймальними силами, що виникають внаслідок різниці густин, і силами міжмолекулярного тертя
де g – прискорення вільного падіння, g = 9,81 м/с2; ℓ – визначальний лінійний розмір поверхні теплообміну, м, для горизонтальних труб – це зовнішній діаметр, а для вертикальної поверхні – висота поверхні; b - температурний коефіцієнт об’ємного розширення теплоносія, К-1; для повітря b = 1/Тп, Тп – абсолютна температура повітря, К; Dt = tc – tп – температурний напір. Критерій Прандтля є мірою подібності полів температури і швидкості у потоці. Він характеризує вплив фізичних властивостей теплоносія на тепловіддачу, залежить тільки від температури і знаходиться за таблицями довідників Pr = n/a, де a = l/(cp×r) – коефіцієнт температуропровідності, м2/с; l - коефіцієнт теплопровідності, Вт/(м×К); ср – масова ізобарна теплоємність, Дж/(кг×К); r - густина, кг/м3. Якщо 103<Ra<108 – режим вільного руху ламінарний, якщо Ra>6×1010 – режим турбулентний. За проміжних значень критерію Релея – режим перехідний (хвильовий). Оскільки коефіцієнт конвективної тепловіддачі aк є складною функцією багатьох змінних, в інженерних розрахунках його визначають за критеріальними рівняннями (рівняннями подібності). Критеріальне рівняння – це залежність між критеріями подібності, що характеризують той чи інший процес. Їх отримують за експериментальними даними методами теорії подібності, згідно з якою для подібних процесів критерії і критеріальні рівняння однакові. Це дає можливість отримувати експериментальні дані на моделях процесів, апаратів, пристроїв, що спрощує дослідження. Коефіцієнт конвективної тепловіддачі входить до критерію Нуссельта, який характеризує інтенсивність тепловіддачі на межі „стінка-теплоносій”: Nu = akℓ/l. (4.3) Критеріальні рівняння подають у вигляді залежності критерію Нуссельта Nu від визначальних критеріїв, до яких входять незалежні змінні величини. Для однофазних теплоносіїв за стаціонарного теплового режиму критеріальне рівняння має вигляд Nu = f(Re,Gr,Pr), а для вільного руху- Nu = f(Gr,Pr) (4.4) Критеріальні рівняння подають у вигляді степеневих функцій. Наприклад, рівняння (4.4) можна подати у вигляді
де с і n – сталі, які залежать від режиму вільного руху та положення поверхні теплообміну у просторі і визначаються за узагальненими дослідними даними. Слід пам’ятати, що критеріальні рівняння виду (4.5) можна використовувати тільки для тих меж зміни аргументів, для яких вони підтверджені дослідами. Поправка критерії Прандтля теплоносія, які знаходять із таблиць фізичних властивостей відповідно за температурою на відтані від стінки за межами рухомого шару tт і біля стінки tc. Для повітря критерій Прандтля практично не залежить від температури, а Nu = c(Gr×Pr)n = cRan. (4.6) Значення с і n, отримані М.О.Міхеєвим експериментально для горизонтальних труб, наведені у табл. 4.1 Таблиця 4.1
Із формули (4.6) видно, що інтенсивність конвективної тепловіддачі за вільного руху залежить головним чином від режиму (інтенсивності) руху. Опис дослідної установки Схема експериментальної установки для вивчення тепловіддачі за вільним рухом повітря у необмеженому просторі показана на рис.4.1. Основним елементом дослідної установки є мідна горизонтальна труба 1 задовжки ℓ мм та зовнішнім діаметром d мм. Усередині труби знаходиться електричний нагрівник 2 з ніхромового дроту, що рівномірно намотаний на керамічну трубку 3 та закріплений на ній. Торці трубки закриті тепло- та електроізоляторами 5. Електронагрівник живиться від мережі змінного струму напругою 220 В через автотрансформатор 6, що дає можливість змінювати потужність, яка вимірюється ватметром 7. Температура поверхні труби вимірюється шістьма хромель-копелевими (хромель – 90% Ni + 10% Cr; копель – 56% Cu + 44% Ni) термопарами 4, гарячі спаї яких розміщені рівномірно на поверхні труби. Температура повітря визначається за термометром 10, розміщеним у приміщенні лабораторії. Електроди термопар виведені до перемикача, за допомогою якого вони почергово підєднуються до цифрового вольтметра 9, яким вимірюють електрорушійну силу (ЕРС). Замість цифрового вольтметра може використовуватись шеститочковий автоматичний самописний потенціометр 8. Температура поверхні труби визначається за верхньою шкалою, а її значення записуються на діаграмній стрічці. Для подальших розрахунків знаходять середню температуру за стаціонарного теплового режиму, тобто коли температура стінки перестає змінюватись з часом. На стендах, де ЕРС термопар вимірюється цифровим вольтметром 9, середня температура стінки труби tc визначається за градуювальними таблицями хромель-копелевих термопар залежно від ЕРС, яку знаходять як суму середньої ЕРС термопар `Е і поправки на температуру холодних спаїв DЕ. Температура холодних спаїв дорівнює температурі повітря у кімнаті tп.
Рис.4.1. Наприклад, середня ЕРС термопар становить `Е=3,87мВ, температура повітря tп = 18°С. За градуювальною таблицею для цієї температури DЕ = 1,18 мВ. Тоді Е = `Е + DЕ = 3,87 + 1,18 = 5,05 мВ. За таблицею tс = 74°С. За критеріальним рівнянням 1. Визначити режим вільного руху. Для цього за рівнянням (4.2) розраховують критерій Релея. Якщо 103<Ra<108 – режим ламінарний, якщо Ra>6.1010 – турбулентний. Фізичні властивості повітря знаходять за табл.4.4 залежно від його температури у приміщенні. За визначальний розмір приймають зовнішній діаметр труби. 2. За табл.4.1 знаходять значення c і n та підставляють їх у критеріальне рівняння (4.6). 3. За отриманим критеріальним рівнянням розраховують критерій Нуссельта. 4. За критерієм Нуссельта визначають розрахунковий коефіцієнт конвективної тепловіддачі 5. Порівнюють розрахунковий та дослідний коефіцієнти конвективної тепловіддачі
Фізичні властивості сухого повітря (рб = 101,3 кПа) Табл. 7
Контрольні запитання 1. Що таке тепловіддача, види тепловіддачі. 2. Які існують види руху теплоносіїв? 3. Режими руху теплоносіїв та їх визначення. 4. Закон Ньютона-Ріхмана для конвективної тепловіддачі. Пояснити усі величини, що входять до рівняння. Які фактори впливають на коефіцієнт конвективної тепловіддачі? 5. Критеріальне рівняння, що описує конвективну тепловіддачу за вільного руху теплоносіїв. Який фізичний зміст критеріїв, що входять до рівняння? 6. Що таке визначальні температура та лінійний розмір? 7. Основні елементи лабораторної установки та їх призначення. 8. У якій послідовності виконується лабораторна робота та опрацювання дослідних даних? 9. Графічне опрацювання дослідних даних.
Лабораторна робота 5
Порядок проведення дослідів 1. Отримати у керівника завдання. 2. Ознайомитись з вимірювальними приладами та визначити ціну поділки шкали кожного з них. 3. За допомогою вентиля 20 або 35 заповнити випарник водою до рівня, заданого керівником. Під час дослідів рівень потрібно підтримувати постійним, добавляючи воду у випарник. 4. Відкрити вентиль 21 для подачі охолодної води у конденсатор вторинної пари. 5. Відкрити вентиль 11 для подачі гріючої пари у випарник і встановити тиск пари, що відповідає першому режиму роботи. Під час дослідів тиск треба підтримувати сталим. 6. Продути через вентиль 1 сепаратор 6. Продувку закінчити, коли із дренажної трубки 34 з¢явиться пара. 7. Аналогічно продути гріючу камеру та парову оболонку вимірника 27 за допомогою вентилів 2 та 30. 8. Відкрити на ¼ оберта вентилі 24 та 26 для видалення із гріючої камери 10 та із конденсатора 19 газів, що не конденсуються. Видалення газів проводити перед кожним дослідом. 9. Злити конденсат із вимірників 27 та 29, для чого відкрити вентилі 31 та 33. 10. Закрити вентилі 31 та 33, і коли у вимірниках з¢явиться конденсат, увімкнути секундомір, одночасно записавши у журнал спостережень початковий об¢єм конденсату у кожному вимірнику. 11. Після закінчення часу першого досліду (задається керівником) записати кінцевий об¢єм конденсату. Об¢єм конденсату, який утворився за час досліду у см3, визначається як різниця між кінцевим та початковим об¢ємами конденсату у вимірнику. 12. Якщо вимірники не заповнені конденсатом, дослід повторити, не зливаючи його. В іншому випадку злити конденсат із вимірників і, не змінюючи режим, повторити дослід. У процесі кожного досліду записувати у журнал спостережень тиск гріючої пари за манометром 12, тиск вторинної пари за манометром 16 і температуру конденсату вторинної пари у вимірнику 29 – за термометром 25. 13. Аналогічно провести досліди за інших режимів, змінивши тиск гріючої пари. 14. Після закінчення останнього досліду: а) закрити вентиль 11 для припинення подачі пари у випарник; б) закрити вентиль 21 для припинення подачі води у конденсатор; в) злити конденсат із вимірників; г) приступити до обробки результатів дослідів. Лабораторна робота №6 Порядок виконання роботи. 4.1. Перевірка приладу на герметичність. Перш ніж почати аналіз, треба довести рівні реактивів у поглинальних посудинах 4 і 6 до позначок, які знаходяться на капілярах над посудинами, під кранами 5. Посудину, в якій треба підняти рівень реактиву, поворотом відповідного крана 5 (при закритих інших кранах) з¢єднують з бюреткою 8 (положення крана II). Бюретку піднімають приблизно до середини висоти штативу і відкривають обидва крани над перехідником 9. Опускаючи зрівнювальну склянку 10, створюють розрідження в обох частинах бюретки, в результаті рівень рідини у поглинальній посудині 6 почне підніматися. Повільно доводять рівень реактиву до позначки, після чого кран 5 закривають (положення крана I). Коли всі поглинальні посудини підготовлені, поворотом крана 1 з¢єднують бюретку з атмосферою. Піднімаючи зрівнювальну склянку 10, доводять рівень запірної рідини в обох частинах бюретки до яких-небудь позначок у верхній її частині. Триходовий кран 1 ставлять в положення III, зрівнювальну склянку опускають якомога нижче і спостерігають за положенням рівня 8 в поглинальних посудинах та вимірювальній бюретці. Якщо рівні рідин впродовж 5 хвилин залишаться незміними, прилад можна вважати герметичним. У разі негерметичності для виявлення місця нещільності газоаналі
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

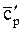 ,
Дж /(м3н·К)
,
Дж /(м3н·К)
 ,
Дж /(кг·К)
,
Дж /(кг·К)
 Дж/(кмоль·К)
Дж/(кмоль·К)
 ,
Дж/(кмоль·К)
,
Дж/(кмоль·К)
 ,
Дж/(кг·К)
,
Дж/(кг·К)
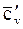 ,
Дж/(м3·К)
,
Дж/(м3·К)
 = 1295 Дж/(м3﹒К).
= 1295 Дж/(м3﹒К). = 29000 Дж/(кмоль﹒К).
= 29000 Дж/(кмоль﹒К). = 20686 Дж/(кмоль﹒К).
= 20686 Дж/(кмоль﹒К). = 713 Дж/(кг﹒К).
= 713 Дж/(кг﹒К).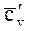 =923 Дж/(м
=923 Дж/(м  ﹒К).
﹒К).

 ,
, ,
, , (4.5)
, (4.5)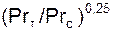 враховує вплив на тепловіддачу зміни теплофізичних властивостей теплоносія біля стінки при нагріванні або при охолодженні, тобто при зміні напрямку теплового потоку; Prт і Prc –
враховує вплив на тепловіддачу зміни теплофізичних властивостей теплоносія біля стінки при нагріванні або при охолодженні, тобто при зміні напрямку теплового потоку; Prт і Prc – , тому рівняння (4.5) набуває вигляду
, тому рівняння (4.5) набуває вигляду
 (рівняння (4.3)).
(рівняння (4.3)).



