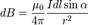Сторонние силы. Электродвижущая сила. Обобщенный закон Ома для неоднородного участка цепи.

Сторонние силы. Электродвижущая сила. Обобщенный закон Ома для неоднородного участка цепи.

Силы неэлектр происх, действ на заряды со стор ист тока, наз сторонними. прир сторон сил мож быть различ.Например в гальв эл, они возн за счет энерг хим реакц межд электродами и эл литами, в генерат за счет мех энерг вращ рот и т.д. сторон силы сов раб по перемещ эл зарядов. Физ велич,опред работой,соверш сторон сила-ми при перемещ единич положит зар, наз ЭДС цепи.ε=A/Q0. Обобщ зак Ома. Рас- смт неоднор уч цепи. Действ э.д.с. на уч 1-2обозн ε12, а прилож на конц уч разн потенц φ1-φ2. тогда раб А сторон и элстат сил равна A=Q0ε12+Q0(φ1-φ2), за вр t в пров выд тепл Q=I(квадр)Rt=IRQ0.из этих формул получ IR=(φ1-φ2)+ ε12, откуда I=

=(φ1-φ2+ ε12)/R. Это выр предст собой зак Ома для неодн уч цепи в инт форме котор явл обобщ законом Ома.

------------------------------------------------------------------

Обобщенный закон Ома в интегральной и дифференциальной формах.

Закон Ома (интегральной форме) для участка электрической цепи имеет вид I=U/R, где – напряжение или разность потенциалов, - сила тока, - сопротивление,

Закон Ома для всей цепи имеет вид I=ξ/(R+r), где ξ – ЭДС источника сопротивления, I - сила тока в цепи, R - сопротивление всех внешних элементов цепи, r - внутренние сопротивление источника напряжения.

Закон Ома (дифференциальной форме)

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

j=σE, где j=I/S вектор плотности тока, σ-удельная проводимость, E-вектор напряженности электрического поля. Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

------------------------------------------------------------------

Работа и мощность постоянного тока. Закон Джоуля-Ленца в интегральной и дифференциальной формах.

Мощность постоянного тока.

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то среднюю мощность можно вычислить по формулам: P=I*U=I^2*R=U^2/R.

Работа тока – работа электрического поля по переносу электрических зарядов вдоль проводника, работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого она совершалась.

Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока: A=U*I*t=I^2*R*t=U^2/R*t

Закон Джоуля-Ленца в интегральной форме.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах.

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка

В математической форме этот закон имеет вид:

, где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ до t₂.

Закон Джоуля-Ленца в дифференциальной форме - удельная мощность тока равна скалярному произведению векторов плотности тока и напряженности электрического поля:

, где s - удельная проводимость; r - удельное сопротивление среды.

Закон Джоуля-Ленца в дифференциальной форме носит совершенно общий характер, т. е. не зависит от природы сил, возбуждающих электрический ток. Закон Джоуля-Ленца, как показывает опыт, справедлив и для электролитов и для полупроводников.

------------------------------------------------------------------

 

Закон Био-Савара-Лапласа. Примеры: Магнитная индукция бесконечно длинного прямолинейного проводника с током и кругового витка.

Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.

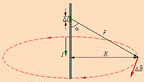
Закон Био́—Савара—Лапла́са играет в магнитостатике ту же роль, что и закон Кулона в электростатике, и глубоко аналогичен ему.

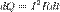
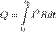
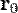Пусть постоянный ток I течёт по контуру γ, находящемуся в вакууме, — точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)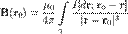

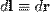Направление dB перпендикулярно плоскости, в которой лежат вектора и r-r0. Направление вектора магнитной индукции может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора dB определяется выражением (в системе СИ)

------------------------------------------------------------------

Сторонние силы. Электродвижущая сила. Обобщенный закон Ома для неоднородного участка цепи.

Силы неэлектр происх, действ на заряды со стор ист тока, наз сторонними. прир сторон сил мож быть различ.Например в гальв эл, они возн за счет энерг хим реакц межд электродами и эл литами, в генерат за счет мех энерг вращ рот и т.д. сторон силы сов раб по перемещ эл зарядов. Физ велич,опред работой,соверш сторон сила-ми при перемещ единич положит зар, наз ЭДС цепи.ε=A/Q0. Обобщ зак Ома. Рас- смт неоднор уч цепи. Действ э.д.с. на уч 1-2обозн ε12, а прилож на конц уч разн потенц φ1-φ2. тогда раб А сторон и элстат сил равна A=Q0ε12+Q0(φ1-φ2), за вр t в пров выд тепл Q=I(квадр)Rt=IRQ0.из этих формул получ IR=(φ1-φ2)+ ε12, откуда I=

=(φ1-φ2+ ε12)/R. Это выр предст собой зак Ома для неодн уч цепи в инт форме котор явл обобщ законом Ома.

------------------------------------------------------------------