Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З дисципліни «теорія автоматичного керування»Содержание книги
Поиск на нашем сайте
1.Перетворити задану структурну схему до одноконтурної та визначити передаточні функції замкнутої системи за керуючою g та збурюючою f діями. 2. Побудувати межі стійкості в площині двох параметрів кx та Tx та вибрати значення цих параметрів, які належать зоні, що може претендувати на стійкість. 3.Дослідити стійкість системи при вибраних значеннях параметрів кx та Tx за методом,що відповідає варіанту завдання. 4.Побудувати перехідні характеристики замкнутої системи за керуючою та збурюючою діями. Дослідити показники якості керування, при необхідності виконати корекцію вибраних значень кx та Tx для покращення показників якості керування. 5. Зробитти перевірку (за керуючою та збурюючою дією). ВАРІАНТ 1
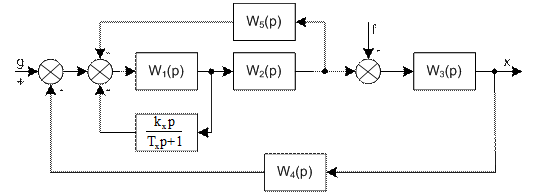
Рис 1. Структурна схема Передаточні функції ланок системи:
Критерій, який досліджується стійкість: Критерій Найквіста Числові значення параметрів передаточних функцій:
ЗАВДАННЯ НА РОЗРАХУНКОВУ-ГРАФІЧНУ РОБОТУ З ДИСЦИПЛІНИ «ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ» 1.Перетворити задану структурну схему до одноконтурної та визначити передаточні функції замкнутої системи за керуючою g та збурюючою f діями. 2. Побудувати межі стійкості в площині двох параметрів кx та Tx та вибрати значення цих параметрів, які належать зоні, що може претендувати на стійкість. 3.Дослідити стійкість системи при вибраних значеннях параметрів кx та Tx за методом,що відповідає варіанту завдання. 4.Побудувати перехідні характеристики замкнутої системи за керуючою та збурюючою діями. Дослідити показники якості керування, при необхідності виконати корекцію вибраних значень кx та Tx для покращення показників якості керування. 5. Зробитти перевірку (за керуючою та збурюючою дією). ВАРІАНТ 2
Рис 1. Структурна схема Передаточні функції ланок системи:
Критерій, який досліджується стійкість: Критерій Найквіста Числові значення параметрів передаточних функцій:
ЗАВДАННЯ НА РОЗРАХУНКОВУ-ГРАФІЧНУ РОБОТУ З ДИСЦИПЛІНИ «ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ» 1.Перетворити задану структурну схему до одноконтурної та визначити передаточні функції замкнутої системи за керуючою g та збурюючою f діями. 2. Побудувати межі стійкості в площині двох параметрів кx та Tx та вибрати значення цих параметрів, які належать зоні, що може претендувати на стійкість.
3.Дослідити стійкість системи при вибраних значеннях параметрів кx та Tx за методом,що відповідає варіанту завдання. 4.Побудувати перехідні характеристики замкнутої системи за керуючою та збурюючою діями. Дослідити показники якості керування, при необхідності виконати корекцію вибраних значень кx та Tx для покращення показників якості керування. 5. Зробитти перевірку (за керуючою та збурюючою дією).
ВАРІАНТ 3
Рис 1. Структурна схема Передаточні функції ланок системи:
Критерій, який досліджується стійкість: Критерій Гурвіца Числові значення параметрів передаточних функцій:
З ДИСЦИПЛІНИ «ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ» 1.Перетворити задану структурну схему до одноконтурної та визначити передаточні функції замкнутої системи за керуючою g та збурюючою f діями. 2. Побудувати межі стійкості в площині двох параметрів кx та Tx та вибрати значення цих параметрів, які належать зоні, що може претендувати на стійкість. 3.Дослідити стійкість системи при вибраних значеннях параметрів кx та Tx за методом,що відповідає варіанту завдання. 4.Побудувати перехідні характеристики замкнутої системи за керуючою та збурюючою діями. Дослідити показники якості керування, при необхідності виконати корекцію вибраних значень кx та Tx для покращення показників якості керування. 5. Зробитти перевірку (за керуючою та збурюючою дією).
ВАРІАНТ 4
Рис 1. Структурна схема Передаточні функції ланок системи:
Критерій, який досліджується стійкість: Критерій Михайлова Числові значення параметрів передаточних функцій:
ЗАВДАННЯ НА РОЗРАХУНКОВУ-ГРАФІЧНУ РОБОТУ
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.190.187 (0.007 с.) |


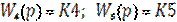



 ;
; 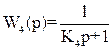 ;
; 



 ;
;