Визначення множини шляхів заданої транзитності

 

В числі обмежень, що накладаються при організації з’єднувальних трактів передавання в мережах зв'язку, може розглядатися обмеження на число транзитних пунктів або транзитних ділянок в них.

Під транзитними пунктами розуміються вузли комутації, що зустрічаються в шляху проходження повідомлення з певного абонентського пункту i в j, в яких відбувається перерозподіл потоків повідомлень. Транзитні ділянки являють собою відповідно лінії зв'язку, що з'єднують транзитні пункти.

Обмеження за транзитністю в шляху передавання повідомлення зумовлюються вимогами до якості обслуговування на мережі (наприклад, до часу проходження повідомлення в мережі, часу опрацювання повідомлення у вузлах комутації тощо).

В термінах графових моделей задача формулюється в такий спосіб.

Нехай дано певний вихідний граф G (N, V), у відповідність з множині N потужністю n вершин якого поставлено вузли комутації мережі зв'язку, а множині V – з'єднувальні лінії мережі.

Необхідно визначити множину шляхів M = { µ_si } із заданої вершини s в решту вершин i N, i≠ s, i =1... n, графа G, для яких параметр транзитности Т не перевищує певної заданої величини T₀, тобто

Т≤ T₀, ∀ µ_si, i≠ s, i=1...n.

 

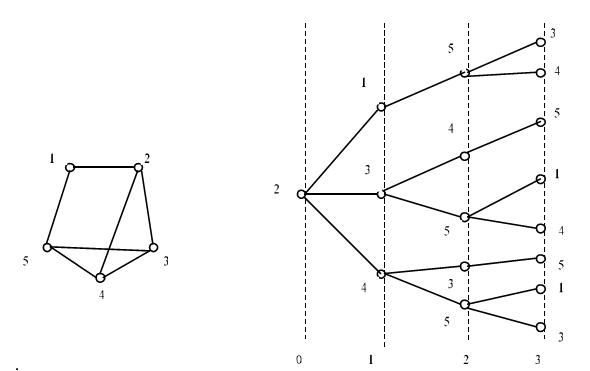
Одним з найбільш зручних і легко зреалізовуваних на ЕОМ методів визначення шляхів, що відповідають цій вимозі, є побудова так званого “ярусного дерева” шляхів від певної заданої вершини s до решти вершин графа.

На рис. 2.10 наведено вихідний граф й відповідне йому “ярусне дерево” з параметром Т₀ =2. Тут під Т розуміється кількість транзитних вершин.

Алгоритм побудови “ярусного дерева” містить в собі такі кроки.

Крок 0. Утворити підмножину нульового яруса, включивши в нього єдиний елемент - вершину s. Використовуючи матрицю суміжності, виписати номери стовбців у рядку з номером S, елементи якої дорівнюють a_sj =1. Таким чином дістано підмножину вершин першого яруса, утворену вершиною s.

 

 

Рисунок 2.10

 

Крок 1. Утворити підмножину вершин наступного яруса. Для цього:

а) по черзі обираються вершини попереднього яруса, для кожної з яких обирається рядок з однойменним номером в матриці суміжності;

б) для кожного рядка виписуються номери стовбців, визначувані ненульовими елементами;

в) у кожному з утворених підмножин виключаються номери вершин (номери стовбців), щодо яких утворювалися підмножини вершин у попередніх ярусах. Всі невикреслені елементи (номери стовбців) утворять підмножини наступного яруса.

Крок 2. Якщо номер яруса дорівнює (Т₀ + 1) – кінець. В противному разі – перейти до кроку 1.

 

Задачі про потоки

 

Задачі про потоки в мережах привертають особливу увагу через специфіку своєї структури. Введемо деякі означення.

О з н а ч е н н я 1. Число х_ij називається потоком по дузі (ребру) (i, j), якщо х_ij ≤ b_ij, де b_ij -пропускна здатність цієї дуги.

О з н а ч е н н я 2. Потоком P_st із певної вершини s, називаної джерелом, в певну вершину t, називану стоком, в мережі є множина негативних чисел х_ij (потоків дуг.

О з н а ч е н н я 3. Перерізом (розрізом) мережі називається ненадлишкова сукупність дуг (ребер), при вилученні яких з мережі порушується її зв'язність.

 

О з н а ч е н н я 4. Пропускною здатністю перерізу називається сума пропускних здатностей дуг, орієнтованих в напрямку від джерела до стоку, або ребер, що складають цей переріз.

О з н а ч е н н я 5. Переріз, що розділяє s та t й має найменшу пропускну здатність, називається мінімальним перерізом.

 

Мінімальний переріз, що розділяє джерело s та стік t, є аналогом “вузького місця” в будь-якій мережі й, отже, величина максимального потоку не може перевищити його пропускну здатність. Існує теорема, доведена Фордом та Фалкерсоном, котра стверджує, що розмір максимального потоку завжди дорівнює мінімальній пропускній здатності серед всіх перерізів, що розділяють s та t. Теорема про максимальний потік та мінімальний переріз є основною в теорії потоків у мережах.

О з н а ч е н н я 6. Мережа, що має одне джерело й один стік, називається двополюсною.

 

О з н а ч е н н я 7. Мережа, у котрої кожна пара вершин може розглядатися як джерело і стік, називається багатополюсною.

 

О з н а ч е н н я 8. Якщо в мережі є декілька джерел і декілька стоків і потік може йти з будь-якого джерела в будь-який стік, то такий потік називається однопродуктовим (наприклад, мережі газопроводів, нафтопроводів, енергомережа тощо).

 

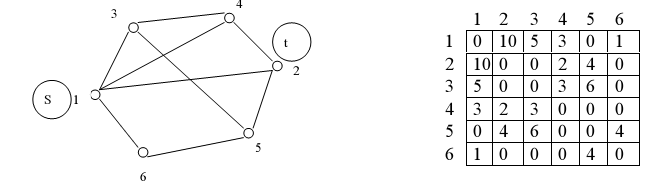
О з н а ч е н н я 9. Якщо в мережі з декількома джерелами і стоками потік має йти з певних виокремлених джерел в певні фіксовані стоки, то такий потік називається багатопродуктовим (наприклад, мережі інформаційного зв'язку, перевезень поштових відправлень тощо).

За будь-якого переміщення деяких об'єктів з одного пункту в інший виникають потоки і, якщо вони розглядаються з урахуванням обмежень на переміщення, виникає природна задача про віднайдення максимальної величини потоку, що може існувати в умовах заданих обмежень. Для оцінення пропускної здатності зв'язуючої мережі досить визначити розмір максимального потоку, що вона може пропустити, причому обчислення його дугових компонентів, віднайдення шляхів передавання може стати зовсім необов'язковим. Згідно з теоремою про максимальний потік і мінімальний розріз, вказана задача може бути зведена до визначення пропускної здатності мінімального перерізу. Найбільш простим засобом віднайдення такого перерізу для двухполюсної мережі є перегляд усіх можливих перерізів, що розділяють множину вершин N мережі на дві незв'язаних підмножини: N₁, що включає джерело, і N₂, що включає стік, і вибір серед них перерізу, який має мінімальну пропускну здатність. Єдину складність, що при цьому виникає, становить визначення множини самих перерізів. Нижче наводиться алгоритм, котрий дає змогу подолати зазначену складність, і має високу ефективність з погляду реалізації на ЕОМ. Основна ідея, покладена в його основу, полягає в наступному.

Вершинам підмножин N₁ і N₂, на які черговий переріз розділяє мережу, надаються певні позначки, наприклад ,: 0 => N₁; 1=> N₂.

Нехай джерело s належить до N₁,а стік t належить до N₂. Отже, вершина s буде позначена нулем, а t – одиницею. Залишається розподілити позначки поміж рештою (n – 2) вершин для кожного можливого перерізу мережі. Для цього слід задатися правилом, котре породжує різні комбінації нулів та одиниць, що можна використовувати для того, щоб розсортувати решту (n – 2) вершин на дві підмножини N₁ та N₂. За таке правило можна використовувати принцип подання чисел натурального ряду в двійковому виді. Розрядність двійкового числа в такому разі визначається значенням (n – 2) й, отже, максимальна кількість двійкових чисел складе 2^(n-2). Ця сама величина відповідає максимально можливій кількості перерізів, котрі розділяють мережу на дві підмножини – N₁ та N₂ несполучених вершин. Кожній позиції двійкового числа слід поставити у відповідність номер вершини (порядок не має значення). Нагадаємо, що вершини s та t тут не беруть участі, оскільки вони вже набули позначок і відповідно до них розподілені в підмножини: s N₁, t N₂.

Алгоритм формулюється в такий спосіб.

Крок 0. Надамо джерелу (вершині s) позначку “0”, а стокові (вершині t) –позначку “1”. Вважаємо значення лічильника перерізів дорівнюваним С = 0.

рок 1. Утворимо двійкове подання числа С і відсортуємо вершини у відповідності з позначками. Визначаємо пропускну здатність перерізу для дістаного варіанта розподілу вершин як суму пропускних здатностей дуг (ребер), що складають розглядуваний переріз.

Крок 2. Збільшуємо значення змінної С на одиницю. Якщо С=2 ^(n-2), перехід до кроку 3, в противному разі – до кроку 1.

Крок 3. Серед дістанох значень {M_i (N₁, N₂)} обираємо найменше.

Розглянемо приклад, що ілюструє роботу алгоритму.

Нехай потрібно оцінити пропускну здатність поміж джерелом s та стоком t в неорієнтованій мережі, модель і матриця пропускних здатностей ребер якої показані на рис. 2.11.

Рисунок 2.11

 

Покладемо S: => 0; t: => 1.

Комбінація позначок вершин для всіх можливих перерізів і величини їхніх пропускних здатностей зведено в таблицю 2.1.

Так, наприклад, нульовий по порядку переріз буде характеризуватися у відповідності з символікою, наведеною в таблиці 2.1, наступним поділом вершин на підмножини:

N₁ =(1, 3, 4, 5, 6); N₂ =(2)

 

Таблиця 2.1 — Визначення пропускної здатності

 

Номери перерізів	Двійкові комбінації
номери вершин

 

 

Цей переріз становлять ребра: (1, 2), (4, 2), (5, 2). Сумарна пропускна здатність цих ребер дорівнює 16. Наступний переріз характеризуется поділом

N₁ =(1, 3, 4, 5); N₂ =(2, 6) Він містить ребра: (1,2), (1,6), (4, 2), (5, 2), (5, 6) котрі изначають пропускну здатність перерізу, відповідно дорівнюючу 21.

Як видно з таблиці 2.1, найменшу величину пропускної здатності має переріз під номером 0. Він і визначає пропускну здатність заданої мережі.

Примітка. Слід зазначити, що вищевикладений спосіб дістання сукупності ребер що входять в певний переріз, породжує ребра, які можуть бути відсутніми у фізичному графі. Ці ребра можна або вилучити з розгляду, або враховувати з нульовими пропускними здатностями.

 

Завдання для самостійної роботи

Дайте стислу відповідь на питання

1. Які завдання відносяться до класу завдань синтезу і які — до класу аналізу?

2. Для чого використовується модельне представлення мережі?

3. Перерахуєте форми модельного представлення телекомунікаційної мережі як об'єкту синтезу і аналізу. Охарактеризуйте кожну з них

4. Що називається графом? Орієнтованим графом? Неорієнтованим графом?

5. Що відображають стосунки суміжності і інцидентності елементів графа?

6. У чому полягає відмітна особливість мережевої моделі?

7. Як, призначення мережі абонентського доступу?

8. Перерахуєте вимоги, яким повинно задовольняти рішення задачі синтезу мережі мінімальної вартості

9. Який граф називається деревом, покриваючим деревом?

10. Сформулюйте ідею алгоритму Пріма, що забезпечує побудову мережі мінімальної вартості

11. Чи можна застосувати алгоритм Пріма для побудови мережі максимальної вартості? Якщо так, то яким чином?

12. Чи можна використовувати алгоритм Пріма при неповнозвязній початковій матриці відстаней? Що це означає?

13. Алгоритм Пріма є точним або евристичним? Яка вершина називається медіаною графа? Що є початковими даними для її визначення?

14. Сформулюйте алгоритм визначення медіани графа по матриці відстаней між всіма парами вершин графа.

15. Яка вершина називається центром графа?

16. Сформулюйте алгоритм визначення центру графа

17. У чому полягає «завдання комівояжера»?

18. Що є точним рішенням «задачі комівояжера»?

19. Який контур називається гамільтоновим циклом?

20. Що називається евристикою? Які алгоритми відносяться до евристичних?

21. Сформулюйте достоїнства і недоліки точних і евристичних алгоритмів.

22. До якого класу завдань відноситься завдання побудови маршрутних матриць?

23. Що називається шляхом в мережі? Довжиною шляху? Транзитністю шляху? Найкоротшим шляхом?

24. Приведіть практичні ситуації, в яких виникає завдання визначення найкоротшого шляху.

25. На чому заснований алгоритм Дейкстри, пошуку найкоротших шляхів?

26. Якого виду позначки використовуються при роботі алгоритму Дейкстри?

27. Чи можна за допомогою алгоритму Дейкстри відшукати безліч шляхів, найкоротших по транзитності? Які початкові дані для цього буде потрібно?

28. Яким методом можна отримати безліч шляхів заданої транзитності?

29. У чому полягає ідея методу побудови ярусного дерева?

30. Що називається потоком з джерела в стік?

31. Дайте визначення перетину мережі.

32. Який перетин називається мінімальним?

33. Сформулюйте теорему про максимальний потік і мінімальний перетин.

34. Яка мережа називається двополюсною? Багатополюсною? Однопродуктової? Багатопродуктовою?

35. У чому відмінність багатополюсної мережі від багатопродуктової?

36. У чому полягає основна ідея оцінки пропускної спроможності мережі?

 

 

Список літератури

 

1. Никитюк Л. А. «Элементы синтеза и анализа телекоммуникационных сетей», методическое пособие, Издательский центр УГАЗ им. А.С. Попова, 2000

2. Стеклов В.К., Кільчицький Є.В. «Основи управління мережами та послугами телекомунікацій», К., «Техніка» 2002

3. Захарченко М. В., Гайворонськая Г. С. «Сети и системы телекоммуникаций», К., «Техника» 2000

4. Васильев Г.А. и др. Логистика М. Экономическое образова, 1993

5. Миротин Л. Б., Ташбаев Ы. Э. и др. Транспортная логистика:Учеб. пособие.— М.: Брандес, 1996.

6. Смехов А. А. Введение в логистику.— М.: Транспорт, 1993.