
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра менеджмента и маркетингаСодержание книги Поиск на нашем сайте
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМ. Н.Г. ЧЕРНЫШЕВСКОГО Кафедра менеджмента и маркетинга С.М. Гвоздева С Т А Т И С Т И К А Учебно-методическое пособие по курсу Саратов - 2009
Учебно-методическое пособие подготовлено в соответствии с положениями и требованиями Государственного образовательного стандарта высшего профессионального образования, включает основные вопросы лекций и семинарских занятий, краткие теоретические положения статистики, основные формулы для решения задач, вопросы и задачи для практических занятий. Для студентов и преподавателей экономических специальностей.
Составитель:
кандидат экономических наук, доцент С.М. Гвоздева
Рекомендуют к печати:
кандидат экономических наук, доцент кафедры менеджмента и маркетинга Леванова Л.Н.
ЧАСТЬ I. ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ Тема 1. Предмет и метод статистики Слово «статистика» латинского происхождения (от status - состояние). В средние века оно означало политическое состояние государства. Как наука статистика возникла в конце 17 века, хотя статистический учет существовал уже в глубокой древности. Так, известно, что еще за 5 тыс. лет до н.э. проводились переписи в Китае, осуществлялось сравнение военного потенциала разных стран, велся учет имущества граждан в Древнем Риме, населения, домашнего имущества, земель – в средние века. Впервые термин «статистика» был введен в обиход в 1749 г. Немецким ученым Г. Ахенвалем, выпустившим книгу о государствоведении. В настоящее время термин «статистика» употребляется в трех значениях. Во– первых, под статистикой понимают особую отрасль практической деятельности людей, направленную на сбор, обработку и анализ данных, характеризующих социально-экономическое развитие страны, ее регионов, отраслей экономики, отдельных предприятий. Во – вторых, статистикой называют науку, занимающуюся разработкой теоретических положений и методов, используемых статистической практикой. В-третьих, статистикой часто называют статистические данные, представленные в отчетности предприятия, публикуемые в сборниках, справочниках, периодической прессе, которые представляют собой результат статистической работы. Особенность статистики заключается в том, что статистические данные сообщаются в количественной форме. Предметом исследования статистики являются массовые явления социально- экономической жизни, она изучает количественную сторону этих явлений в неразрывной связи с их качественным содержанием в конкретных условиях места и времени. Рассмотрим основные понятия, используемые в статистике. 1. Статистическая совокупность – совокупность социально-экономических объектов или явлений общественной жизни, объединенных некой качественной основой, но отличающиеся друг от друга отдельными признаками. Каждая совокупность состоит из отдельных явлений, которые называются единицами совокупности. 2. Единица совокупности – первичный элемент стат. совокупности, являющимся носителем признаков, подлежащих регистрации. В зависимости от изучаемых закономерностей единица совокупности должна иметь единую сущность (однокачественность). 3. Признак – качественная особенность единицы совокупности. Особенностью стат. исследования является то, что в нем изучаются только варьирующие признаки, т.е. признаки, принимающие различные значения. Вариация – это изменение («колеблемость») величины либо значения признака при переходе от одной единицы совокупности к другой. 4. Статический показатель – понятие (категория), отображающее количественные характеристики соотношения признаков общественных явлений. Статистические показатели следует отличать от стат. данных. Стат. данные – это конкретные численные значения стат. показателей. Совокупность приемов, пользуясь которыми статистика исследует свой предмет, составляет метод статистики. Можно выделить три группы статистических методов: 1) метод массовых наблюдений; 2) метод группировок; 3) обработка статистических показателей.
Тема 2. Статистическое наблюдение Формы, виды наблюдения. В статистической практике используют две формы стат. наблюдения: 1) отчетность - составная часть государственной статистики. Отчетность представляется в соответствии с государственной программой статистических работ. Отчетность устанавливается для конкретных субъектов рынка – предприятий, организаций. Для нее характерны обязательность. За достоверность данных отчетности предприятия и организации несут ответственность. 2)специально организованное статистическое наблюдение. Примерами служат переписи населения. В СССР было осуществлено семь таких переписей: в 1920, 1926, 1939, 1959, 1970, 1979, 1989 годах. Также к ним следует отнести выборочное социально-демографическое обследование населения на 1 января 1985 г., микроперепись населения 1994 г. С точки зрения полноты охвата фактов различают: - сплошное статистическое наблюдение, когда производится полный учет всех единиц изучаемой совокупности. - несплошное статистическое наблюдение – учет части единиц совокупности, на основе которой можно получить обобщающую характеристику всей совокупности. Одним из видов несплошного наблюдения является способ основного массива, когда отбирают наиболее крупные единицы наблюдения, в которых сосредоточена значительная доля всех подлежащих изучению фактов (например, динамика цен может быть исследована по наиболее крупным городам или наиболее крупным оптовым, розничным рынкам). Вторым видом несплошного наблюдения является выборочное наблюдение - это наблюдение, при котором характеристика всей совокупности дается по некоторой ее части, отобранной в случайном порядке. По времени наблюдения выделяют: - непрерывное статистическое наблюдение – вид наблюдения, которое проводится, когда необходимо зарегистрировать все единицы по мере их возникновения (регистрация актов гражданского состояния – рождений, браков, смертей и т.д.); - единовременное наблюдение проводится по мере возникновения потребности в сборе данных, в исследовании конкретного явления или процесса. Если наблюдение проводится через определенные промежутки или периоды времени, то такое наблюдение является периодическим. 4. Ошибки стат. наблюдения. Ошибки стат. наблюдения по источнику происхождения можно подразделить на следующие: 1) преднамеренные. Они завышают или занижают конкретные значения признака или показателя. 2) непреднамеренные. Они в свою очередь подразделяются на следующие: А) случайные. Они связаны с невнимательностью регистратора, небрежностью в заполнении документов и т.д. Б) систематические. Они возникают при округлении при подсчете данных наблюдения. В) репрезентативности (представительности) – рассмотрим в теме «Выборочное наблюдение».
Классификация группировок В зависимости от решаемых задач различают следующие группировки: - типологические – выделение в составе массового явления тех его частей, которые однородны по качеству и условиям развития. В результате такой группировки выделяют социально-экономические типы. Примерами такой группировки могут служить группировки хозяйственных объектов по формам собственности, безработных по уровню образования, занятых по уровню доходов. - структурные группировки предназначены для изучения состава или структуры изучаемого явления, они позволяют осуществлять расчленение отдельных совокупностей с целью изучения их состава. Например, при изучении населения по проблемам занятости определяется удельный вес численности мужчин и женщин в объеме всей совокупности. В зависимости от числа, положенных в основу группировочных признаков выделяют: простые и комбинационные группировки. Если в основу группировки положен один группировочный признак, такую группировку называют простой. Если группировка построена по двум и более признакам, такую группировку называют комбинационной. Среди простых группировок особо выделяются ряды распределения. Ряд распределения – это группировка, в которой для характеристики групп применяется один показатель – численность групп. Ряды, построенные по атрибутивному (качественному) признаку, называются атрибутивными рядами распределения. Ряды распределения, построенные по количественному признаку, называются вариационными рядами. В зависимости от вида группировочных признаков различают группировки по количественным и качественным признакам. Качественный признак отражает определенные свойства, качества данного явления и записывается в виде текста (например, группировки населения по полу, семейному положению и т.д.). Статистические таблицы Статистические таблицы являются средством наглядного выражения результатов исследования. Таблицы отличаются наглядностью, а статистической ее называют потому, что она отражает результаты сводки массовых наблюдений. Статистическая таблица имеет подлежащее и сказуемое. Подлежащее таблицы – это перечень единиц совокупности или группы, т.е объект изучения. Сказуемым таблицы являются цифровые данные, характеризующие подлежащее. Обычно подлежащее располагается слева в виде названия строк, сказуемое вверху – в виде названия граф.
Рис. 1. Макет статистической таблицы. По построению подлежащего таблицы могут быть: - простыми – статистические таблицы, в подлежащем которых нет группировок. Простые таблицы могут быть: а) простые перечневые, когда в подлежащем находится перечень единиц, составляющих объект изучения; б) территориальные – дается перечень территорий, стран, городов и т.д.; в) хронологические – в подлежащем приводятся периоды времени или даты. - групповыми – таблицы, в которых статистическая совокупность расчленяется на отдельные группы по какому либо одному признаку, причем каждая из групп может быть охарактеризована рядом показателей; - комбинационные – таблицы, где в подлежащем дана группировка единиц совокупности по двум и более признакам, взятым в комбинации. Требования к составлению и оформлению таблиц: 1. Таблица по возможности должна быть краткой. Не следует загружать ее излишними подробностями, затрудняющих анализ исследуемых явлений. 2. Каждая таблица должна иметь подробное название, из которого становится известно: а) какой круг вопросов излагает и иллюстрирует таблица; б) каковы географические границы статистической совокупности, представленные таблицей; в) каков период времени, за который приведены данные, или момент времени, к которому они относятся; г) каковы единицы измерения, если они одинаковы для всех табличных клеток. 3. Первые графы, содержащие подлежащее, обозначаются заглавными буквами алфавита. Заглавия строк подлежащего и граф сказуемого таблицы записываются по возможности полностью. Заголовки граф следует сформулировать так, чтобы были ясны смысл данной величины и порядок ее расчета. 4. Приводимые в подлежащем и сказуемом признаки должны быть расположены в логическом порядке с учетом необходимости рассматривать их совместно. Обычный принцип размещения – от частного к общему, т.е. сначала показывают слагаемые, а в конце подводят итоги (если это необходимо). Когда приводятся не все слагаемые, а лишь наиболее важные из них, применяется противоположный принцип: сначала показывают общие итоги, а затем выделяют наиболее важные части («В том числе», «Из них»). Следует отличать «Итого» и «Всего». «Итого» является итогом для определенной части совокупности, «Всего» - итог для совокупности в целом. 5. Таблица может сопровождаться примечаниями, в которых указываются источники данных, более подробно раскрываются содержание показателей, а также оговорки в случае, если таблица содержит данные, полученные в результате вычислений.
Абсолютные величины Изучая массовые общественные явления, статистика в своих выводах опирается на числовые данные, полученные в конкретных условиях места и времени. Результаты статистического наблюдения регистрируются прежде всего в форме первичных абсолютных величин. Абсолютные показатели являются всегда именованными числами, т.е. имеют какую-либо единицу наблюдения: - натуральные единицы наблюдения применяют в тех случаях, когда единица измерения соответствует потребительским свойствам продукта. Например, производство тканей оценивается в квадратных метрах, автомобилей – в штуках и т.д. - условно-натуральные единицы применяются, если некоторые разновидности продукта обладают общностью основного потребительского свойства. Например, в тоннах условного топлива определяется общий объем потребленного на предприятии топлива, при этом пересчет производится на 100% содержание какого-либо вещества. - стоимостные (денежные) единицы измерения широко используются при обобщении учетных данных. Относительные величины Относительный показатель – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных (относительных) величин. Условные обозначения, применяемые для вычисления относительных величин: y1 – фактический уровень показателя в отчетном периоде; y0 – фактический уровень показателя в базисном периоде; yпл(1) – плнируемый уровень показателя в отчетном периоде; yпл (0) – планируемый уровень показателя в базисном периоде. Выделяют основные виды относительных величин: 1. Относительная величина динамики – характеризует изменение уровня развития какого-либо явления во времени. Она которая находится по формуле: 2. Относительная величина планового задания: 3. Относительная величина степени выполнения плана: 4. Относительные величины структуры характеризуют долю относительных частей в общем объеме совокупности, их рассчитывают как отношение числа единиц в отдельных частях совокупности к общей численности единиц (или объему признака) по всей совокупности. 5. Относительные величины координации характеризуют соотношение между частями одного целого (напр., соотношение между численностью городского и сельского населения). 6. Относительная величина наглядности отражает результат сопоставления одноименных показателей, относящихся к одному и тому же периоду времени, но к разным объектам или территориям. 7. Относительная величина интенсивности – отношение между разноименными абсолютными величинами (напр., фондовооруженность труда, потребление продуктов питания на душу населения). Одно из главных требований, которое предъявляется при исчислении относительных величин, заключается в необходимости обеспечения сопоставимости сравниваемой величины и величины, принятой за базу сравнения. Прежде всего должна быть обеспечена сопоставимость по методологии расчета сравниваемых показателей, по степени охвата объектов исследуемой совокупности и т.д. Тема 5. Средние величины Виды средних величин Средние величины делятся на два больших класса: 1) степенные средние. К ним относятся такие наиболее известные и часто применяемые виды, как средняя арифметическая, средняя гармоническая, средняя квадратическая; 2) структурные средние, в качестве которых рассматриваются мода и медиана. Степенные средние в зависимости от представления исходных данных исчисляются в двух формах: простой и взвешенной. Простая средняя считается по несгруппированным данным и имеет следующий вид:
где xi - варианта (значение) осредняемого признака, m – показатель степени средней, n – число вариант. Взвешенная средняя высчитывается для сгруппированных данных и имеет вид:
где fi – частота, показывающая, сколько раз встречается i-ое значение осредняемого признака. Наиболее часто используемая для расчета среднего значения какого – либо явления или процесса – средняя арифметическая. В этом случае показатель степени средней m=1. Формулы для расчета средней величины имеют вид: а) средняя арифметическая простая: б) средняя арифметическая взвешенная: Если m=-1, то в этом случае вычисляется средняя гармоническая. Она имеет две разновидности: а) средняя гармоническая простая: б) средняя гармоническая взвешенная: К средним величинам, кроме степенных средних, относят также моду и медиану. Мода (Мо) – это наиболее часто встречающее значение признака у единиц данной совокупности. Медиана (Ме) – лежит в середине ранжированного ряда и делит его пополам. Расчет медианы по несгруппированным данным производится следующим образом: 1) расположить индивидуальные значения признака в возрастающем порядке; 2) определить порядковый номер медианы по формуле: В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода и медиана. Для определения их величины используются следующие формулы:
где ХМо – начало модального интервала; h – шаг интервала; fMo – частота, соответствующая модальному интервалу; f(-1)- предмодальная частота; f(+1)- послемодальная частота.
где XMe – нижняя граница медианного интервала; S(-1) – накопленная частота интервала, предшествующего медианному; fMe – частота медианного интервала. Показатели вариации Показатели вариации делятся на две группы: - абсолютные (размах вариации, среднее линейное отклонение, среднее квадратическое отклонение); - относительные (коэффициент колеблемости, коэффициент вариации). 1. Наиболее простым является расчет показателя размаха вариации: h = x max – x min. Для более точной оценки колеблемости определяют среднее абсолютное и среднее квадратической отклонение. Смысл этих показателей в общем одинаков: они показывают на сколько в среднем отклоняются отдельные значения признака от их средней величины. Среднее линейное отклонение имеет две разновидности: - среднее линейное отклонение простое: - среднее линейное отклонение взвешенное: Этому показателю присущ следующий недостаток – он недостаточно четко реагирует на отклонение вариационного признака. Поэтому в статистической практике наиболее часто для оценки колеблемости используют среднее квадратическое отклонение. Среднее квадратическое отклонение имеет две разновидности: - среднее квадратическое простое применяется для несгруппированных данных и имеет вид:
- среднее квадратическое взвешенное применяется, если данные сгруппированы и рассчитывается по формуле:
К относительным показателям вариации относятся: - коэффициент колеблемости, который рассчитывается следующим образом:
где - коэффициент вариации находится по формуле:
Для характеристики вариационных рядов могут использоваться квартили, квантили и децили. Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% - между Q2 и Q3; и остальные 25% превосходят Q3. Квартили определяются по формулам, аналогичным приведенной выше формуле для расчета медианы:
где S(-1) – сумма накопленных частот интервалов, предшествующих интервалу, в котором находится первая квартиль;
Условные обозначения те же, что и для величины Q1. При расчете квантиль совокупность разбивается на 5 частей, децилей – на 10 частей. Простая случайная выборка Теорема П.Л. Чебышева доказывает принципиальную возможность определения генеральной средней по данным простой случайной выборки Согласно теореме А.Я.Ляпунова при достаточно большом числе независимых наблюдений в генеральной совокупности вероятность того, что расхождение выборочной и генеральной средней не превзойдет величину Приведем наиболее часто употребляемые уровни доверительной вероятности и соответствующие значения t для выборок достаточно большого объема (n> 30):
1. Средняя ошибка выборки для среднего значения находится двумя способами, в зависимости от того, способом производился отбор в выборочную совокупность:
- при повторном отборе средняя ошибка выборки для среднего значения равна:
- при бесповторном отборе:
Предельная ошибка выборки для среднего значения находится по формуле: где t – коэффициент доверия,
2. Средняя ошибка выборки для доли признака находится двумя способами, в зависимости от того, способом производился отбор в выборочную совокупность: - при повторном отборе средняя ошибка выборки для доли признака равна:
где w – выборочная доля. - при бесповторном отборе средняя ошибка выборки для доли признака равна:
Предельная ошибка выборки для доли признака находится по формуле: где Доверительный интервал для генеральной средней можно записать так:
Аналогичным образом могут быть записаны доверительные пределы генеральной доли:
Малая выборка При уменьшении объема выборки снижается точность оцениваемых параметров генеральной совокупности. Для оценки возможных пределов ошибки малой выборки пользуются отношением Стьюдента:
где S - среднее квадратическое отклонение в выборке; n – 1 – число степеней свободы (k). Если tрасч. по модулю tнабл.., то можно сделать вывод, что с определенной вероятностью оценки параметров генеральной совокупности значимы. В таблице приведены величины отношения Стьюдента t: Таблица Величины отношения Стьюдента t (краткая выдержка)
Средняя квадратическая ошибка выборки для среднего значения при повторном отборе составляет:
Средняя ошибка выборки для среднего значения при бесповторном отборе равна:
Средняя ошибка выборки доли признака при повторном отборе находится по формуле: Средняя ошибка выборки доли признака при бесповторном отборе рассчитывается как: Тема 9. Индексы Понятие индексов Индекс – это относительная величина, показывающий во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления ив других условиях, получаемый в результате сопоставления уровней сложных социально – экономических показателей во времени, в пространстве или с планом. По степени охвата элементов совокупности различают индивидуальные и сводные индексы. Индивидуальные индексы – индексы, характеризующие изменение только одного элемента совокупности.(индивидуальные индексы обозначаются - i). Сводный (общий) индекс отражает изменение по всей совокупности элементов сложного явления. Обозначают сводный индекс символом I. В зависимости от содержания и характера индексируемой величины различают индексы количественных и качественных показателей. Объемные, суммарные показатели, выражающиеся абсолютными показателями являются количественными. Показатели, рассчитанные на какую-то единицу, условно называют качественными. При вычислении индексов различают сравниваемый уровень и уровень, с которым производится сравнение, называемый базисным. Возможны два варианта расчета индексов – цепной и базисный. Цепные индексы получают сопоставлением текущих уровней с предшествующим. Таким образом, база сравнения непрерывно меняется. Базисные индексы получают сопоставлением с уровнем периода, принятого за базу сравнения. В зависимости от методологии расчета различают агрегатные индексы и средние из индивидуальных индексов. Агрегатные индексы качественных показателей могут быть рассчитаны как индексы переменного и постоянного составов. Средние из индивидуальных индексов, в свою очередь, делятся на средние арифметические и средние гармонические индексы. Индивидуальные индексы Индивидуальный индекс – это индекс, характеризующий изменение однородных экономических явлений во времени. Условные обозначения:
Существует последовательное индексирование с помощью двух методов: последовательным и базисным.
В первом случае мы рассмотрели индивидуальный индекс цен цепной (последовательное индексирование), во втором - индивидуальный индекс цен базисный. С аналитической точки зрения индивидуальный индекс цен цепной показывает во сколько раз происходит увеличение (уменьшение) цен в последующем периоде по сравнению с предыдущим, базисный - во сколько раз происходит увеличение (уменьшение) цен в отчетном периоде по сравнению с базисным. Свойства индивидуальных индексов: 1. Произведение последовательных цепных индексов дает соответствующий базисный индекс. 2. Частное от деления последовательного базисного индекса от предшествующего дает соответствующий индекс. 3. Индивидуальный индекс произведения двух или более сомножителей равен произведению индексов данных сомножителей. Общие индексы Если известно, что изучаемое явление неоднородно и сравнение уровней можно произвести только после приведения их к общей мере, экономический анализ выполняют посредством общих индексов. Рассмотрим наиболее используемые в экономическом анализе общие индексы товарооборота, цен, физического объема. Общий индекс товарооборота характеризует во сколько раз произошло увеличение товарооборота в отчетном периоде по сравнению с базисным за счет двух факторов (цен и физического объема товарооборота):
Общий индекс цен характеризует во сколько раз произошло увеличение товарооборота в отчетном периоде по сравнению с базисным за счет изменения цен:
Общий индекс физического объема товарооборота характеризует во сколько раз произошло увеличение товарооборота в отчетном периоде по сравнению с базисным за счет изменения физического объема товарооборота:
Абсолютное изменение товарооборота рассчитывается по формулам: 1) абсолютное изменение товарооборота за счет изменения двух факторов (цен и физического объема продукции):
2) абсолютное изменение товарооборота за счет изменения цен:
3) абсолютное изменение товарооборота за счет изменения физического объема продукции:
Индексы средних величин Выделяют следующие виды индексов средних величин: 1. Индекс переменного состава- индивидуальный индекс, который отражает изменения средней величины в целом и представляет собой результат совокупного изменения двух факторов (цены и количества):
2. Индекс постоянного состава отражает изменение средней цены за счет изменения собственно цен по отдельным единицам совокупности:
3. Индекс структурных сдвигов отражает изменение средней цены за счет изменения физического объема товарооборота:
Тема 10. Ряды динамики Рядом динамики (динамическим рядом, временным рядом) называется последовательность значений статистического показателя, упорядоченная в хронологическом порядке. Отдельные наблюдения временного ряда называют уровнями этого ряда. Каждый ряд динамики содержит значения времени и соответствующие им значения уровней ряда. В зависимости от характера временного параметра ряды делятся на моментные и интервальные. В моментных рядах динамики уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные интервалы (периоды) времени. Важной особенностью интервальных рядов динамики абсолютных величин является суммирования их уровней. Уровни рядов динамики могут представлять собой абсолютные, относительные и средние величины. Если уровни ряда представляют собой не непосредственно наблюдаемые значения, а производные величины (средние или относительные), то такие ряды называют производными. Одним из важнейших условий, необходимых для правильного отражения временным рядом реального процесса развития, является сопоставимость уровней ряда. При анализе изменений явлений во времени на практике часто определяют средние показатели, в том числе средний уровень ряда. Средний уровень ряда определяется по-разному для моментных и интервальных рядов динамики. Для интервальных рядов динамики с равноотстоящими во времени уровнями расчет проводится по формуле простой средней арифметической:
где n – число уровней или длина ряда, yi - уровень ряда динамики. В случае моментных рядов динамики с равностоящими во времени уровнями средний уровень находится по формуле средней хронологической взвешенной:
где yi - уровни ряда динамики, y0 , yn - соответственно начальный и конечный уровни ряда, n - число уровней или длина ряда. На практике для количественной оценки динамики явлений широко применяется ряд основных аналитических показателей: абсолютные приросты, темпы роста, темпы прироста. Каждый из указанных показателей бывает трех видов: цепной, базисный, средний. В основе расчета этих показателей динамики лежит сравнение уровней временного ряда. Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными. Если сравнение осуществляется при переменной базе и каждый последующий уровень сравнивается с предыдущим, то вычисленные таким образом показатели называются цепными. Абсолютный прирост равен разности двух сравниваемых уровней и характеризует величину изменения показателя за определенный промежуток времени. Абсолютный прирост может быть представлен в виде:
где уt –текущий уровень ряда динамики, yб- базисный уровень динамики, уt-1- предшествующий уровень динамики. Средний абсолютный прирост является обобщающей характеристикой скорости изменения исследуемого показателя во времени. Для его определения за весь период наблюдения используется следующая формула:
где yn, y1 - соответственно конечный и начальный уровни ряда динамики. Темп роста Т характеризует отношение двух сравниваемых уровней ряда. Темп роста может быть представлен в виде:
где yi - текущий уровень ряда динамики. Средний темп роста является обобщающей характеристикой динамики и отражает интенсивность изменения уровней ряда. Он показывает сколько в среднем процентов последующий уровень составляет от предыдущего в течение всего периода наблюдения:
Темп прироста характеризует абсолютный прирост в относительных величинах и показывает, на сколько процентов изменился сравниваемый уров
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.104.106 (0.013 с.) |


 .
.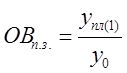 .
. .
.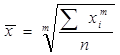 ,
, ,
, ;
;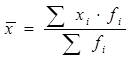
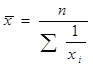
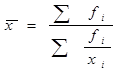
 .
.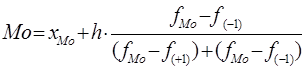 ,
, ,
, ;
;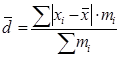 .
. ;
; .
. ,
,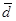 - среднее абсолютное отклонение;
- среднее абсолютное отклонение;  - среднее значение для х.
- среднее значение для х.
 ,
, - нижняя граница интервала, в котором находится первая квартиль;
- нижняя граница интервала, в котором находится первая квартиль; .
.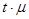 , равна интегралу Лапласа (Ф(t)). Величину
, равна интегралу Лапласа (Ф(t)). Величину  называют предельной ошибкой выборки и обозначают ∆.
называют предельной ошибкой выборки и обозначают ∆. ;
;
 .
. ,
, - средняя ошибка выборки для среднего значения.
- средняя ошибка выборки для среднего значения. ,
, .
.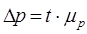 ,
, - средняя ошибка выборка для доли признака.
- средняя ошибка выборка для доли признака.
 .
. ,
,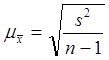 ;
; .
. .
.
 - цена в отчетном периоде,
- цена в отчетном периоде, - цена в базисном периоде,
- цена в базисном периоде,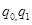 - физический объем товарооборота в базисном и отчетном периоде соответственно,
- физический объем товарооборота в базисном и отчетном периоде соответственно,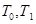 - товарооборот в базисном и отчетном периоде.
- товарооборот в базисном и отчетном периоде. ;
; 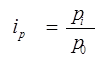 .
.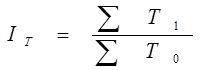 =
=  .
.

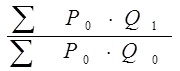 .
.





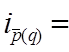
 .
. ,
, ,
,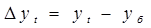 (по базисной системе),
(по базисной системе), (по цепной системе),
(по цепной системе), ,
,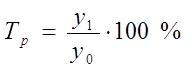 (по базисной системе),
(по базисной системе), (по цепной системе),
(по цепной системе),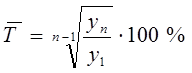 .
.


