
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование дифференцирующейСодержание книги
Поиск на нашем сайте И ИНТЕГРИРУЮЩЕЙ ЦЕПЕЙ
Цель работы Экспериментальное исследование преобразования формы прямоугольных импульсов с помощью дифференцирующей и интегрирующей цепей.
Краткие теоретические сведения Дифференцирующей цепью называется линейный четырехполюсник, напряжение на выходе которого пропорционально первой производной входного напряжения:
где A — постоянная величина, имеющая размерность времени. Интегрирующей цепью называется линейный четырехполюсник, напряжение на выходе которого пропорционально интегралу входного напряжения:
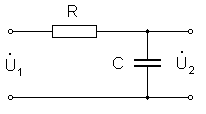
Дифференцирование и интегрирование может быть осуществлено при помощи цепей из последовательно соединенных индуктивности и активного сопротивления (цепи RL) или последовательно соединенных емкости и активного сопротивления (цепи RC), при выполнении определенных условий в отношении постоянных времени этих цепей. Наибольшее распространение получили дифференцирующие и интегрирующие цепи RC, так как конденсатор по сравнению с катушкой индуктивности имеет меньшую стоимость. 2.1. Дифференцирующая цепь. На рис. 1 изображена RС дифференцирующая цепь.
Рис. 1
Коэффициент передачи дифференцирующей цепи равен
или где w0=1/RC. Модуль коэффициента передачи, называемый амплитудно-частотной характеристикой, равен
При частоте w=w0 активное и реактивное сопротивления цепи равны и модуль коэффициента передачи равен 1/(2)1/2. Фазочастотная характеристика дифференцирующей цепи равна
На рис. 2 показаны частотные характеристики дифференцирующей цепи. В области частот RCw<<1 коэффициент передачи равен
Рис. 2
Переходной характеристикой называют отклик цепи, т. е. напряжение на выходе при подаче на вход единичного скачка напряжения. Используя преобразование Лапласа, нетрудно показать, что переходная характеристика любой дифференцирующей цепи имеет вид при t³0
где Т=RC — постоянная времени. Предположим, что на вход цепи подано переменное напряжение U1 в виде двухполярных прямоугольных импульсов (рис. 3) длительностью Т/2 (Т-период). Тогда напряжение на выходе цепи U2 будет изменяться по закону (рис. 3): при 0<t<T/2 при T/2<t<T Если длительность полупериода Т/2 равна RC, то напряжение в конце каждого экспоненциального спада равняется 0,37U1.
Рис. 3
2.2. Интегрирующая цепь. На рис. 4 показана схема RC интегрирующей цепи.
Рис. 4
Коэффициент передачи равен
где w0=1/RC соответствует частоте, при которой активное и реактивное сопротивления интегрирующей цепи равны. Выражения для амплитудно-частотной и фазочастотной характеристик имеют вид
В области частот RCw>>1 коэффициент передачи имеет вид
что соответствует операции интегрирования. На рис. 5 приведены частотные характеристики интегрирующей цепи. Рис. 5
Переходная характеристика интегрирующей цепи равна
где T=RC — постоянная времени цепи. Предположим, что на вход цепи подано переменное напряжение U1 в виде двухполярных прямоугольных импульсов (рис. 5) длительностью Т/2 (Т-период).
Рис. 6
Тогда напряжение на выходе цепи U2 будет изменяться по закону (рис. 5): при 0<t<T/2 при T/2<t<T При Т/2=RC напряжение U2 в моменты времени, кратные Т/2 и Т, равно по модулю |0,63U1|.
Экспериментальная схема На рис. 7 приведена экспериментальная схема лабораторной работа. Напряжение синусоидальной формы со звукового генератора с помощью диодных ограничителей преобразуется в прямоугольные импульсы. Переключатель S1 служит для переключения исследуемой цепочки. Переключатели S2-5 служат для переключения комбинаций RC цепочек. Исследуемое напряжение с выхода цепочек поочередно подается на вход электронного осциллографа.
Рис. 7
Порядок выполнения работы 4.1. Собрать схему по рис. 7, включить осциллограф и звуковой генератор. 4.2. Проверить форму сигнала на входе и выходе диодного ограничителя. Регулировкой уровня выходного напряжения звукового генератора установить форму импульсов, близкую к прямоугольной. 4.3. Исследовать дифференцирующую цепь. Вход осциллографа подключить к выходу дифференцирующей цепи. Изменяя частоту сигнала звукового генератора, добиться экспоненциального спада импульсов до 0,37 от амплитудного значения. Определить длительность спада. Зарисовать осциллограмму. Аналогичные измерения провести для всех комбинаций RC (R1C1, R1C2, R2C1, R2C2). Рассчитать постоянные времени и сравнить с полученными экспериментально. 4.4. Исследовать интегрирующую цепь. Переключить вход осциллографа к выходу интегрирующей цепи. Установить частоту звукового генератора так, чтобы амплитуда импульсов равнялась 0,63 от амплитуды входных импульсов. Измерить длительность импульса. Зарисовать осциллограмму. Проделать аналогичные измерения для всех комбинаций RC (R3C3, R3C4, R4C3, R4C4). Рассчитать постоянные времени и сравнить с измеренными.
Содержание отчета Результаты работы представить в виде таблицы, с рассчитанными и измеренными постоянными времени дифференцирующих и интегрирующих цепей. Приложить зарисованные осциллограммы.
6. Контрольные вопросы 1. Какая цепь называется дифференцирующей? 2. Как изменяется напряжение на выходе идеальной дифференцирующей цепи при подаче на вход: синусоидального, трапецеидального и прямоугольного напряжения? 3. Изобразите RC дифференцирующую цепь. Какому требованию должна отвечать эта цепь? 4. Какая цепь называется интегрирующей? 5. Изобразите RC интегрирующую цепь. Какому требованию должна отвечать эта цепь? 6. Как изменяется напряжение на выходе идеальной и реальной интегрирующей цепи при подаче прямоугольного напряжения?
Литература 1. Манаев Е. И. Основы радиоэлектроники. М.: Советское радио, 1976. Лабораторная работа № 5
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.009 с.) |

 , (1)
, (1) . (2)
. (2)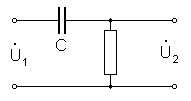
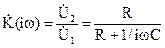 , (3)
, (3)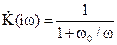 , (4)
, (4) . (5)
. (5) . (6)
. (6)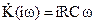 . Из теории операционного исчисления известно, что это соответствует дифференцированию входного напряжения сигнала, т. е. выходное напряжение пропорционально первой производной входного сигнала с коэффициентом пропорциональности RC.
. Из теории операционного исчисления известно, что это соответствует дифференцированию входного напряжения сигнала, т. е. выходное напряжение пропорционально первой производной входного сигнала с коэффициентом пропорциональности RC.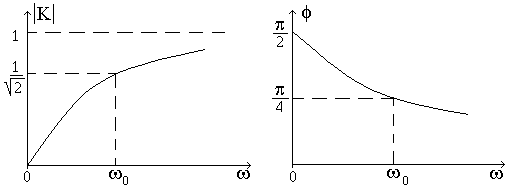
 , (7)
, (7)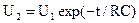 ,
,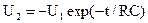 .
.
 , (8)
, (8) , (9)
, (9)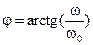 . (10)
. (10) , (11)
, (11)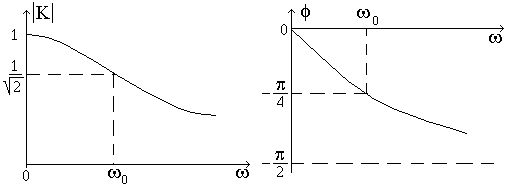
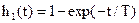 , (12)
, (12)
 ,
, .
.



