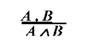Логічні відношення між складними судженнями

17. Види дедуктивних умовиводів(силогізм, полісилогізм, ентимема).

Силогізм як вид дедуктивного умовиводу вартий особливої уваги. Змалюємо структуру простого силогізму. Він складається з суб’єкта – меншого за об’ємом терміну (S), предикату – більшого за об’ємом терміну (P) і середнього терміну (M), який не входить до висновку, але входить до обох посилок, забезпечуючи між ними логічний зв’язок, виступаючи опосередкованою ланкою і уможливлюючи зв’язок S і Р.

Всі люди (М) – смертні (Р)

Сократ (S) – людина (М)

Сократ (S) смертний (Р).

Крім простого силогізму існує також складний силогізм (полісилогізм), який складають кілька простих силогізмів, які певним чином пов’язані між собою.

Всі рослини – живі організми

Всі квіти - рослини

Всі квіти – живі організми (висновок 1) полісилогізм

Троянда – квітка

Троянда – живий організм (висновок № 2)

Скорочений силогізм без однієї посилки має назву “ентимема”. У ентимемі може бути також відсутнім висновок. Така ентимема зокрема застосовується тоді, коли висновок людина робити не хоче в силу його очевидності, або небажаності.

Всі колекціонери – збирачі. Третьяков – збирач (відсутня друга посилка).

Всі співаки – люди. Ф. Кіркоров – співак (відсутнє заключення).

18. Поняття відношення логічного слідування

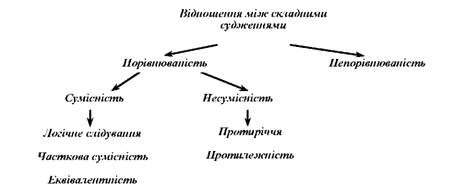
Логічне слідування – одне з фундаментальних відносин між висловлюваннями по формі, що використовується для перевірки правильності міркувань.

Поняття логічного слідування лежить в основі будь-якої теорії правильних міркувань. Міркування (умовивід) вважається правильним, якщо і тільки якщо його посилки (Γ) і висновок (В) перебувають у відношенні логічного слідування, тобто з посилок логічно випливає висновок.

Введене вище визначення логічного слідування дозволяє перевіряти правильність будь-яких міркувань за умови, що, по-перше, встановлено процедуру виявлення логічної форми, і, по-друге, є ефективний спосіб приписування значень нелогічних параметрам, що дозволяє врахувати всі можливі їх інтерпретації. Зазвичай для забезпечення цих умов будуються логічні теорії (наприклад, логіка висловлювань або логіка предикатів), в яких дається конкретизація фундаментальних логічних понять (і логічного слідування в тому числі) стосовно до даної теорії.

19. Правила умовиводів логіки судження

Правилом висновку є норма, що дозволяє із суджень однієї логічної структури як засновків отримувати судження певної логічної структури як висновок.

Правила висновку логіки висловлювань поділяються на:

Основними називаються правила, які змістовно очевидні і дозволяють відрізнити правильно побудовані міркування від неправильно побудованих міркувань.

Похідними називаються правила, які виводяться із основних і сприяють скороченню процесу висновку.

 

У свою чергу основні та похідні правила поділяються на:

Прямими називаються правила, які вказують на безпосереднє виведення висновку із засновків.

Непрямими називаються правила, які дають можливість стверджувати правомірність деяких висновків на основі визнання правомірності інших висновків.

Правило введення кон'юнкції (ВК):

Правило введення диз'юнкції (ВД):

 

Правило транзитивності імплікації (ТІ):

 

 

20. Безпосередні умовиводи

Безпосередні умовиводи.

До безпосередніх умовиводів відносять:

а) обернення, перетворення, протиставлення предикату;

б) умовиводи за логічним квадратом.

До опосередкованих умовиводів відносять простий категоричний силогізм.

Безпосереднім умовиводом називається дедуктивний умовивід, у якому висновок отримують із одного засновку.

О берненням називається такий безпосередній умовивід у висновку якого суб'єктом стає предикат засновку, а предикатом - суб'єкт засновку.

В умовиводі шляхом п е р е т в о р е н н я ми отримуємо висновок де суб'єктом є суб'єкт засновку, а предикатом є поняття, що суперечить предикату засновку. Це стає можливим завдяки зміні якості засновку.

Протиставленням предикату називається такий безпосередній умовивід у результаті якого отримують висновок суб'єктом якого є поняття, що суперечить предикату засновку, а предикатом стає суб'єкт засновку.

Умовиводи за "логічним квадратом".Нагадаємо, що таких відношень існує чотири види: підпорядкування, суперечності, противності і підпротивності.

Умовиводи, які будуються із урахуванням цих 4-х типів відношень між категоричними судженнями, називають умовиводами за "логічним квадратом".
21. Простий категоричний силогізм

Уперше систематичний розгляд теорії висновку дає Арістотель в "Аналітиках", вона отримала назву "силогістика".

К а т е г о р и ч н и м с и л о г і з м о м називають дедуктивний умовивід, який складається із двох засновків і висновку, представлених судженнями виду: ASP, ESP, ISP, OSP.

Термін, що входить до висновку як його суб'єкт називається м е н ш и м і позначається буквою S.

Термін, який виконує роль предиката висновку називається б і л ь ш и м і позначається буквою Р.

Термін, що входить в обидва засновки, але відсутній у висновку, називається с ер е д н і м і позначається буквою М.

У нашому прикладі більший засновок 1, а менший - 2. Виходячи із зазначеного, структуру силогізму можна записати у вигляді імплікації, де антецедентом буде кон'юнкція засновків, а консеквентом - висновок:

Ці схеми називають фігурами категоричного силогізму, тобто різновидами категоричного силогізму, які визначаються розташуванням середнього терміна.

Різновиди категоричного силогізму розрізняють за формами засновків і висновку. їх прийнято називати модусами категоричного силогізму.

При побудові категоричного силогізму дотримуються певних правил, які поділяються на:

а) загальні правила категоричного силогізму і

б) спеціальні правила фігур.

22. Види індуктивних умовиводів

До недедуктивних умовиводів відносяться:

- індуктивні умовиводи та

- умовиводи за аналогією.

а) Індуктивні умовиводи.

І н д у к т и в н и м умовиводом називається умовивід, в якому із одиничних або часткових суджень виводиться загальне судження.

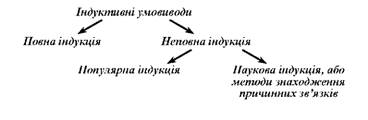
П о в н о ю індукцією називається такий умовивід, у якому на підставі притаманності ознаки кожному предметові деякої множини робиться висновок про належність цієї ознаки всім предметам цієї множини.

Н е п о в н о ю індукцією називається умовивід, у якому висновок про весь клас предметів базується на вивченні тільки деяких предметів, що належать до даного класу.

23. Аналогія як умовивід

А н а л о г і я - це такий не дедуктивний умовивід, у якому судження про притаманність певної ознаки деякому об'єктові виводиться на основі подібності цього об'єкту з іншим об'єктом.

З р а з к о м аналогії називається об'єкт ознака якого переноситься на другий об'єкт.

Су б' є к т о м аналогії називається об'єкт на який переноситься ознака.

До структури аналогії входять чотири види суджень:

1) судження про наявність основи у зразка;

2) судження про наявність основи у суб'єкта;

3) судження про наявність переносної ознаки у зразка;

4) судження про наявність переносної ознаки у суб'єкта. Перші три судження - це засновки, а четверте судження - це висновок аналогії.

Існує два види аналогій:

- Аналогією властивостей називається такий умовивід, в якому переносною ознакою є властивість

- Аналогією відношення називається умовивід в якому переносною ознакою є ознака відношення.

24. Види доведення

П р я м и м називається доведення, в якому теза безпосередньо випливає із аргументів.

Пряме доведення застосовують тоді, коли наявна достатня кількість аргументів.

Не п р я м и м доведенням називається такий вид доведення у якому істинність тези випливає із хибності антитези.

А н т и т е з о ю називають положення, яке суперечить тезі.

Розрізняють два види непрямого доведення:

- апагогічні та розділові.

Апагогічне доведення іноді називають доведенням від супротивного.

Наступним видом непрямого доведення є розділове доведення.Його суть полягає в побудові розділового судження, одним із елементів якого є теза.

25. Види спростування

С п р о с т у в а н н я м називається така логічна операція, за допомогою якої встановлюють хибність або необгрунтованість тези.

Існує три види спростування:

а) Спростування тези.

Спростування тези фактами.