
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение проверочной матрицыСодержание книги
Поиск на нашем сайте
Приведем матрицу H к треугольному виду:
Система уравнений:
Информационные символы: Защитные символы: Порождающая матрица Информационные символы и соответствующие им защитные:
Есть черный ящик. L – совокупность преобразований в нем
Св-во линейности кодов – сумма двух разрешенных кодовых слов равна разрешенному слову. Билет 5. Предположение, что множество
(здесь через 0 обозначен единичный элемент группы Каждая строка в (1) образующими элементами соответствующих смежных классов. Если в качестве образующих 0, е1, е2,..., еs взяты элементы минимального веса в своем смежном классе, то любая последовательность Для доказательства предположим, что x=yi+е, где е - элемент минимального веса в своем смежном классе. Очевидно, d{yi. x)=w (e) и d(yk,x)=w(yk-yi-e). Если е— единственный элемент минимального веса, тоd(yi, x)<d(yk, x) для всех K¹ i. Если таких элементов несколько (например, w( yj +e)=w(e)), то d(yi, x)=d(yk, x) то при условии, что yk= yj –yi. Следовательно, для каждого элемента yj +e минимального веса в смежном классе, содержащем e, найдется слово yk= yj –yi, которое находится от у на расстоянии d(yk, i)=w(e). Таким образом, для всех последовательностей x, входящих в 1-й столбец стандартной расстановки, условная вероятность Р( x \yi) максимальна. Если x находится в смежном классе с несколькими элементами минимального веса, то условная вероятность Р( x \уi)=Р( x \уk) и остается максимальной для всех уk, находящихся на одинаковом расстоянии от x Правило декодирования может быть сформулировано следующим образом: найти выходную последовательность канала xÎ Очевидно, это правило совпадает с декодированием по максимуму правдоподобия и, следовательно, является оптимальным. Правило декодирования линейного кода можно сформулировать так: после того. как выходная последовательность x; найдена в (1), определить наиболее вероятный вектор ошибки e, отыскивая образующий элемент того смежного класса, который содержит x; переданную последовательность найти из соотношения y=x—e. Можно построить аналогичную процедуру декодирования, если воспользоваться однозначным соответствием между смежными классами и синдромами образующих элементов. Правило декодирования заключается в следующем: вычислить синдром принятой последовательности S= x HT =eHT, где e — образующий элемент смежного класса, содержащего x. По найденному синдрому S найти e; определить у из соотношения у= x —e. Такое декодирование также совпадает с декодированием по максимуму правдоподобия и, следовательно, остается оптимальным. Первыми кодами с подобной процедурой декодирования были коды Хемминга, исправляющие одиночные ошибки. Однако отыскание последовательности ошибок, когда число допустимых ошибок больше одной, быстро усложняется и при достаточно длинных кодах и большом количестве исправляемых ошибок становится практически невозможным.
Билет 6. Проблема передачи непрер. сообщ-я закл. в получ. его копии на приемном пункте. Не сущ-ет способа, позвол-го получить точную копию перед-ого сообщ-я, поск. это требует бесконечной точности его воспроизв-я. Поэт. задают точность воспр-я перед-ого сообщ-я. e-энтропии – это min кол-во инфы, кот. необх. передать по каналу, чт. восст. сообщение с заданной точностью при заданном распределении p(x) источника. Модель передачи непр. сообщ-я:
d2 = e2 – ошибка при восст-нии сообщения y(t). Нужно установить связь м\д x(t) и x’(t), такую, чтобы x’ несло как можно меньшую инфу об x, но обеспечивало заданную точность. H e = min I (x, x’) p(x/x’)
Каждому интервалу ставится в соотв-ие число. чем > n, тем > интервалов и > точность. I(x,x’)=H(x’) – H(x’/x) -взаимная инфа по опред-ию. H(x’/x) = 0 т.к. значение случайной величины x определяет значение случайной величины x’. (“при фиксированном x ”) I(x,x’)= H(x’) - кличество взаимной информации между множествами x и x’ равно энтропии x’. (опр-ся инф-ой ёмкостью регистра). Пусть х равномерно распр. на интевале [a;b] тогда все x’ равновероятны. (b-a)/ log[(b-a)/ Надо обеспечить точность d2 (среднеквадр. ошибка):
Пусть x и x’ непрерывны. (1) x = x’ – n, где n – погрешн. кот. получается в рез-те апроксимации x x’-ом. n=0, n2=d2e=e2 –заданная ошибка He =H(x)-max(H(n)), H(n) будет max при гауссовском распр. n H(n)=[log2ped2n]/2 Источник чаще всего им. гауссовское распр. с d2, тогда: H(n) = [log2ped2x - log2ped2n]/2 = log(d2x/d2n)/2 = log(d2x/e2)/2 [бит/отсчёт] Если за 1с. перед-ся 2F отсчётов, то Нet = 2F He = F*log(d2x/e2) [бит/c] По т.Шеннона для гаусс. канала: Нet < F log(1+q2) [бит/c]
Билет 7. Кол-во информации, кот. Yj несет об Xi = кол-ву информации, кот. Xi несет об Yj. И эта информация называется взаимной информацией м-у Yj и Xi: Для каждой пары (Xi,Yj) соответствует свое кол-во информации, а т.к. Xi и Yj – случайные величины, то и это кол-во информации случайно. Поэтому мы можем ввести понятие средней информации м-у множествами:
Отдельное состояние – это пара чисел I(X,Y)–полная взаимная информация (всегда ≥0, когда системы независимы). Сделаем тождественные преобразования:
Тогда, взаимную информацию м. записать:
С точки зрения информационного описания системы связи безразлично, какую из подсистем рассматривать в качестве передатчика, а какую в качестве приемника. Поэтому энтропии Н (Х) и H (Y) можно интерпретировать как информацию, которая поступает в канал связи, а условные энтропии H (X/Y), H (Y/X) как информацию, которая рассеивается в канале. Согласно теореме I (Х, Y)≥0 мы получаем из (*):
Произвольную кусочно непрерывную функцию
если энергия функции Бесконечная система действительных функций Система нормированных функций в которой каждые две различающихся функции взаимно ортогональны, называется ортонормированной системой. При аппроксимации функции
достигает минимума. Минимум среднеквадратичной ошибки достигается в том случае, когда коэффициенты ряда определяются по формуле Ортогональная система называется полной, если путем увеличения количества членов в ряде среднеквадратичную ошибку можно сделать сколь угодно малой. Таким образом, по счетному множеству коэффициентов точностью восстановить соответствующую функцию Последнее равенство является обобщением теоремы Пифагора на случай n-мерного пространства. Путем непосредственных вычислений легко установить, что энергия сигнала Таким образом, дискретизацией называется замена непрерывной функции Выбор системы ортогональных функций С целью передачи сигнала по каналу связи широко применяется разложение функции образующие систему ортогональных функций, отличаются друг от друга только сдвигом по оси времени t на величину кратную
которую в результате тождественных преобразований можно привести к виду: Если дискретизации подлежит нормальный (гауссов) случайный процесс, энергетический спектр которого имеет прямоугольную форму, то коэффициенты Таким образом, непрерывные сообщения можно передавать в цифровом виде, то есть в виде последовательности чисел, при этом каждое число приближенно выражает величину соответствующего коэффициента Билет 8.
Относительной (дифференциальной) энтропией случайной величины Х называется величина
В частности, если интервал d = 1, то
Выясним физический смысл относительной энтропии H(X). Пусть источник сообщений вырабатывает последовательность значений случайной величины Х. После квантования получим последовательность значений случайной величины X ’: Xi1,Xi2…..Xik…..Xin. При неограниченном увеличении длины последовательности с вероятностью, равной единице, появляются только типичные последовательности, число которых
где Энтропию в дискретном случае можно было определить через число типичных последовательностей:
Аналогично относительную энтропию можно определить через объем VT, занимаемый типичными последовательностями:
В отличие от дискретного случая относительная энтропия может быть не только положительной, но и отрицательной, а также равной нулю. Чем больше объем VT, занимаемой типичными последовательностями, тем больше неопределенность того, какая из них появится. Единичному объему (VT =1) соответствует энтропия (неопределенность), равная нулю (H(X) =0). Это значение принимается за начало отсчета относительной энтропии. В частности, относительная энтропия случайной величины с равномерным на единичном интервале (d = 1) распределением равна нулю:
В этом случае область n -мерного пространства, занимаемая типичными последовательностями, примерно совпадает с областью определения всех последовательностей и имеет форму куба единичного объема (VT = d n = 1). Билет 9.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.42.99 (0.007 с.) |







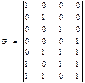
 . L подействовала на X.
. L подействовала на X. x1 и x2 не взаимодействуют между собой, поэтому это линейная система.
x1 и x2 не взаимодействуют между собой, поэтому это линейная система. выходных последовательностей канала является
выходных последовательностей канала является  -мерным векторным пространством над полем GF(q}, а множество Y(n, R) входных последовательностей (код) является подпространством размерности nR. существенно облегчает декодирование. В этом случае Y(n,R) является подгруппой аддитивной группы
-мерным векторным пространством над полем GF(q}, а множество Y(n, R) входных последовательностей (код) является подпространством размерности nR. существенно облегчает декодирование. В этом случае Y(n,R) является подгруппой аддитивной группы  может быть разложено на смежные классы по подгруппе
может быть разложено на смежные классы по подгруппе  . Пусть
. Пусть  — все элементы
— все элементы  (кодовые слова), тогда все элементы множества
(кодовые слова), тогда все элементы множества  (1)
(1) из i-гo столбца отличается от у в меньшем числе разрядов, чем. от любого другого слова
из i-гo столбца отличается от у в меньшем числе разрядов, чем. от любого другого слова 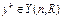 i¹K. Если в смежном классе, содержащем x, существует несколько элементов минимального веса, то найдется столько же кодовых слов, отличающихся от x в одном и том же наименьшем числе разрядов.
i¹K. Если в смежном классе, содержащем x, существует несколько элементов минимального веса, то найдется столько же кодовых слов, отличающихся от x в одном и том же наименьшем числе разрядов.

 x = (b-a)/2n.
x = (b-a)/2n. при min кол-ве взаимной инфы. Связь м\б x и x’ опр-ся кол-вом и длиной интервалов
при min кол-ве взаимной инфы. Связь м\б x и x’ опр-ся кол-вом и длиной интервалов  . И она м.б. >0,<0,=0, в зависимости от средней информации.
. И она м.б. >0,<0,=0, в зависимости от средней информации.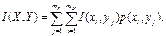
 .
.

 , (*)
, (*)
 -когда X и Y независимы, т.е. взаимн. инф-я =0
-когда X и Y независимы, т.е. взаимн. инф-я =0 , изображающую сообщение или сигнал, можно разложить в обобщенный ряд Фурье по полной системе ортонормированных функций
, изображающую сообщение или сигнал, можно разложить в обобщенный ряд Фурье по полной системе ортонормированных функций
 конечна[9].
конечна[9]. называется ортогональной на отрезке [ a, b ], если
называется ортогональной на отрезке [ a, b ], если  при
при  , а отдельная функция
, а отдельная функция  называется нормированной, если
называется нормированной, если  .
.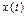 ограничиваются, как правило, конечным числом членов ряда. При заданной системе функций
ограничиваются, как правило, конечным числом членов ряда. При заданной системе функций  можно выбрать такими, при которых среднеквадратичная ошибка аппроксимации
можно выбрать такими, при которых среднеквадратичная ошибка аппроксимации
 . Ряд, с определяемыми таким образом коэффициентами, называется обобщенным рядом Фурье.
. Ряд, с определяемыми таким образом коэффициентами, называется обобщенным рядом Фурье. . Указанную последовательность можно интерпретировать как вектор в n — мерном Евклидовом пространстве с координатами
. Указанную последовательность можно интерпретировать как вектор в n — мерном Евклидовом пространстве с координатами 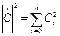 .
. .
. с ограниченным спектром, может быть тождественно представлена счетнывм числом ее значений, взятых через интервал времени
с ограниченным спектром, может быть тождественно представлена счетнывм числом ее значений, взятых через интервал времени 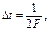 где F — верхняя граничная частота спектра сигнала. В этом случае функции
где F — верхняя граничная частота спектра сигнала. В этом случае функции  ,
, , при этом каждая из них достигает своего максимального значения в те моменты времени, когда значения всех остальных функций равны нулю. Коэффициенты разложения определяются по формуле
, при этом каждая из них достигает своего максимального значения в те моменты времени, когда значения всех остальных функций равны нулю. Коэффициенты разложения определяются по формуле ,
, , то есть
, то есть  будут статистически независимыми случайными величинами, которые совпадают со значениями случайной функции
будут статистически независимыми случайными величинами, которые совпадают со значениями случайной функции 


 - число элементарного n -мерного кубика. Конец вектора, изображающего типичную последовательность, является внутренней точкой этого кубика. Произведение
- число элементарного n -мерного кубика. Конец вектора, изображающего типичную последовательность, является внутренней точкой этого кубика. Произведение  равно объему некоторой области в n -мерном пространстве, внутренние точки которой изображают концы типичных векторов (последовательностей). При
равно объему некоторой области в n -мерном пространстве, внутренние точки которой изображают концы типичных векторов (последовательностей). При  , стремящемся к нулю, число типичных последовательностей стремится к бесконечности, а объем каждого элементарного кубика стремится к нулю. При этом объем VT, занимаемый типичными последовательностями, остается постоянным, равным
, стремящемся к нулю, число типичных последовательностей стремится к бесконечности, а объем каждого элементарного кубика стремится к нулю. При этом объем VT, занимаемый типичными последовательностями, остается постоянным, равным  .
.






