
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 3. Элементы аналитической геометрии и векторной алгебры
Раздел 3. Элементы аналитической геометрии и векторной алгебры Элементы векторной алгебры 1. Определение вектора. Линейные операции над векторами
Определение. Вектором (на прямой, на плоскости, в пространстве) называется упорядоченная пара точек А, В, или направленный отрезок. Точка А называется началом вектора, точка В - его концом. Вектор, начало и конец которого совпадают, называется нуль-вектором. Векторы обычно обозначаются или двумя большими буквами со стрелкой или чертой наверху, или малой буквой также со стрелкой или чертой наверху: Определение. Длина отрезка Определение. Два ненулевых вектора Определение. Коллинеарные векторы называются одинаково (противоположно) направленными, если (в случае принадлежности разным прямым) их концы лежат по одну сторону (по разные стороны) от прямой, соединяющей их начала, а в случае принадлежности одной прямой, если из двух лучей, определяемых этими векторами, один содержится (не содержится) в другом. Обозначение Определение. Два вектора Легко проверить выполнение трех аксиом отношения эквивалентности для понятия равенства векторов: 1) Отложить вектор Определение. Суммой Обозначение:
Для двух векторов Операция сложения векторов ассоциативна и коммутативна, так как при любом порядке откладывания векторов - слагаемых мы придем к тому же самому результату. Определение. Произведением действительного ненулевого числа l на ненулевой вектор
Произведение любого вектора на нуль и нуль-вектора на любое число, по определению, есть нуль-вектор, т.е.
Справедливы следующие свойства умножения вектора на число: 1) справедливые для любых чисел
Декартова прямоугольная система координат. Скалярное произведение векторов. Векторное произведение двух векторов. Смешанное произведение трех векторов. Виды уравнений прямой и плоскости в декартовой системе координат Общее уравнение прямой на плоскости Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
В зависимости от значений постоянных - - - - - Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Уравнение прямой по точке и нормальному вектору В декартовой прямоугольной системе координат вектор с координатами Пример. Найти уравнение прямой, проходящей через точку Для
Нормальное уравнение прямой Если обе части уравнения
нормальное уравнение прямой. Знак ± нормирующего множителя следует выбирать так, чтобы Пример. Дано общее уравнение прямой
уравнение этой прямой с угловым коэффициентом: (делим на 5):
нормальное уравнение прямой:
Заметим, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат. Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2. Уравнение прямой имеет вид:
Раздел 3. Элементы аналитической геометрии и векторной алгебры Элементы векторной алгебры 1. Определение вектора. Линейные операции над векторами
Определение. Вектором (на прямой, на плоскости, в пространстве) называется упорядоченная пара точек А, В, или направленный отрезок. Точка А называется началом вектора, точка В - его концом. Вектор, начало и конец которого совпадают, называется нуль-вектором. Векторы обычно обозначаются или двумя большими буквами со стрелкой или чертой наверху, или малой буквой также со стрелкой или чертой наверху: Определение. Длина отрезка Определение. Два ненулевых вектора Определение. Коллинеарные векторы называются одинаково (противоположно) направленными, если (в случае принадлежности разным прямым) их концы лежат по одну сторону (по разные стороны) от прямой, соединяющей их начала, а в случае принадлежности одной прямой, если из двух лучей, определяемых этими векторами, один содержится (не содержится) в другом. Обозначение Определение. Два вектора Легко проверить выполнение трех аксиом отношения эквивалентности для понятия равенства векторов: 1) Отложить вектор Определение. Суммой Обозначение:
Для двух векторов Операция сложения векторов ассоциативна и коммутативна, так как при любом порядке откладывания векторов - слагаемых мы придем к тому же самому результату. Определение. Произведением действительного ненулевого числа l на ненулевой вектор
Произведение любого вектора на нуль и нуль-вектора на любое число, по определению, есть нуль-вектор, т.е.
Справедливы следующие свойства умножения вектора на число: 1) справедливые для любых чисел
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.250.115 (0.006 с.) |
 ,
, 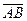 ,
,  ,
,  . Первая из двух букв означает начало вектора, вторая - его конец.
. Первая из двух букв означает начало вектора, вторая - его конец. называется длиной или модулем вектора и обозначается
называется длиной или модулем вектора и обозначается  или
или  .
. называются коллинеарными, если они лежат на одной или на параллельных прямых. Обозначение:
называются коллинеарными, если они лежат на одной или на параллельных прямых. Обозначение:  , 2)
, 2) 
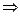
 , 3)
, 3) 
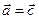 .
. , равный вектору
, равный вектору 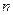 векторов
векторов  называется вектор
называется вектор  , получающийся следующим построением: от произвольной точки А (прямой, плоскости, пространства) откладываем первый вектор
, получающийся следующим построением: от произвольной точки А (прямой, плоскости, пространства) откладываем первый вектор  , равный вектору
, равный вектору  , от конца
, от конца 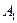 вектора
вектора  , равный вектору
, равный вектору 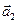 и т.д.: суммой
и т.д.: суммой  последнего отложенного вектора
последнего отложенного вектора 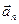 .
. .
. или
или  , удовлетворяющий следующим трем условиям:
, удовлетворяющий следующим трем условиям:
 =
=  ,
,  =
= 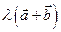 =l
=l  ; 2)
; 2) 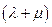
 =
= 
 и любых векторов
и любых векторов 
 Это уравнение называют общим уравнением прямой.
Это уравнение называют общим уравнением прямой. и
и  возможны следующие частные случаи:
возможны следующие частные случаи: – прямая проходит через начало координат;
– прямая проходит через начало координат; - прямая параллельна оси
- прямая параллельна оси  ;
; – прямая параллельна оси
– прямая параллельна оси  ;
; – прямая совпадает с осью
– прямая совпадает с осью  – прямая совпадает с осью
– прямая совпадает с осью  перпендикулярен прямой, заданной уравнением
перпендикулярен прямой, заданной уравнением  Он называется нормальным вектором прямой.
Он называется нормальным вектором прямой. перпендикулярно вектору
перпендикулярно вектору  .
.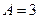 и
и  уравнение прямой примет вид:
уравнение прямой примет вид:  . Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем
. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем  . Следовательно
. Следовательно  . Искомое уравнение запишется в виде
. Искомое уравнение запишется в виде  .
.
 разделить на число
разделить на число  , называемое нормирующем множителем, то получим
, называемое нормирующем множителем, то получим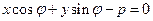 –
– где
где  – длина перпендикуляра, опущенного из начала координат на прямую, а
– длина перпендикуляра, опущенного из начала координат на прямую, а  - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
- угол, образованный этим перпендикуляром с положительным направлением оси Ох. Записать различные типы уравнений этой прямой. Уравнение этой прямой в отрезках:
Записать различные типы уравнений этой прямой. Уравнение этой прямой в отрезках: или
или 
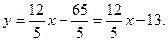
 ;
; 
 ,
,  Значение
Значение  не подходит по условию задачи. Следовательно,
не подходит по условию задачи. Следовательно, 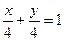 или
или 



