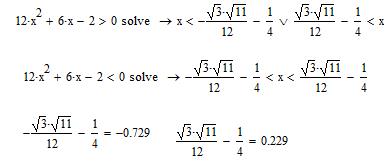Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование функции и построение её графика
Санкт-Петербургский государственный политехнический университет Институт энергетики и транспортных систем Кафедра атомной и тепловой энергетики
КУРСОВОЙ ПРОЕКТ
Дисциплина: Информатика Тема: Исследование функций в математическом пакете MathCAD
Выполнил студент гр. 13221/4 А.Ю.Безумов Руководитель А.В.Ившин
‹‹__››________2014 г. Санкт-Петербург Содержание Введение. 4 Исследование функции и построение её графика. 4 1) Построение графика функции. 4 2) Область определения функции. 4 3) Область значения функции и точки экстремума. 4 4) Чётность и нечётность функции. 5 5) Периодичность функции. 6 6) Асимптоты функции. 6 7) Промежутки выпуклости и вогнутости функции. 6 8) Промежутки монотонности функции. 7 Заключение. 7 Список литературы.. 8
Введение Для выполнения данной курсовой работы используется программа MathCAD, которая предназначена для выполнения сложных математических и инженерных вычислений. В этой курсовой работе необходимо выполнить анализ функции
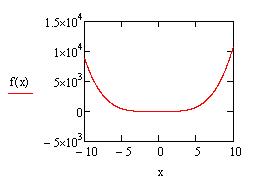
1) Построение графика функции. На рисунке 1 представлен график функции
Рис.1. График функции
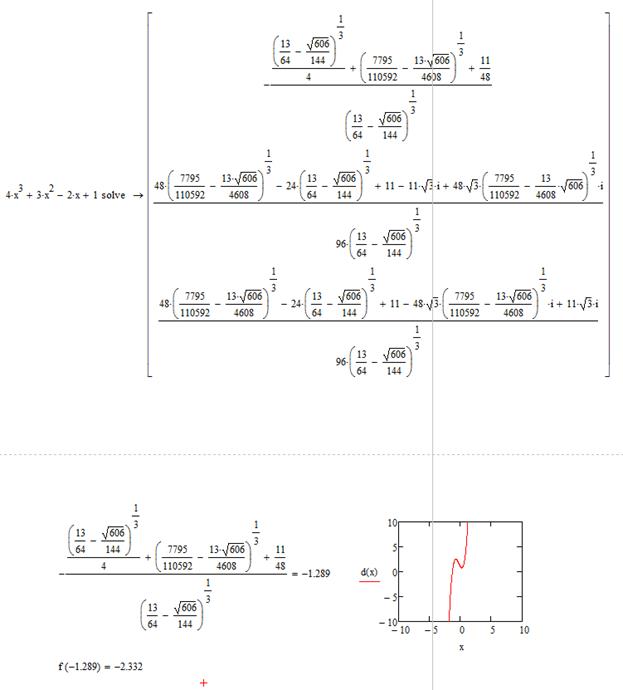
2) Область определения функции. Функция определена при любых значениях х. 3) Область значения функции и точки экстремума. Минимальное значение функция принимает в точке минимума(точка экстремума). Для нахождения экстремума продифференцируем функцию и найдем её корни. Полученное значение x и есть значение аргумента функции, при котором функция принимает наименьшее значение. На рисунке 2 представлены математические операции при нахождении точки минимума функции. Из этого следует, что область значений функции E(f(x))=
Рис.2. Дифференцирование функции и нахождение точек экстремума
4) Чётность и нечётность функции. Функция не является чётной или нечётной f(x)≠f(-x) и -f(x). Функция
5) Периодичность функции. Функция является периодичной, если существует такое число t, что выполняется равенство f(x)=f(x+t). Данная функция не является периодичной, что видно из её графика, так как не существует такого числа t, при котором выполнялось бы равенство f(x)=f(x+t).
6) Асимптоты функции. Асимптот функция не имеет.
7) Промежутки выпуклости и вогнутости функции. Функция является вогнутой в промежутке на промежутке (-∞;-0.729) и (0.229;+∞) и выпуклая на промежутке (-0.729;0.229).Данные получены вследствие приравнивания второй производной к нулю.
Рис.3. Математические операции
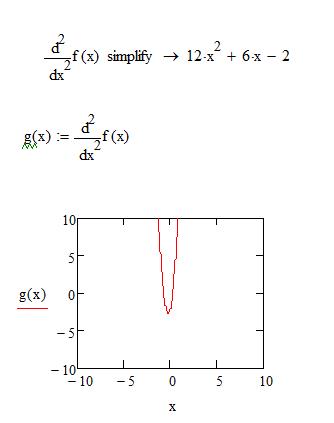
Рис.4. График второй производной функции f(x)
8) Промежутки монотонности функции. Функция монотонно возрастает на интервале (-∞;-1.289) и монотонно убывает (-1.289;+∞).
Заключение MathCad является удобным средством для математических и графических исследований. Построив график функции и рассмотрев его, выясняется, что данная функция определена только на интервале (-∞;+∞), асимптот не имеет, возрастает на (-∞;-1.289), убывает на (-1.289;+∞). Функция является выпуклой на (-0.729;0.229), вогнута на (-∞;-0.729) и (0.229;+∞), имеет одну точку минимума x=-1.289. Список литературы 1. Гурский, Турбина "Вычисления в MathCAD." 2. Макаров "Инженерные расчеты в MathCAD."
|
||||||||||||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 8; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.158.98 (0.005 с.) |
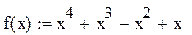 , а именно: найти область значений и определения функции, найти точки экстремума и т.п.
, а именно: найти область значений и определения функции, найти точки экстремума и т.п.