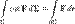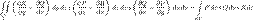Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение кратного интегралаСодержание книги
Поиск на нашем сайте
22) Производная по направлению
Материал из Википедии — свободной энциклопедии У этого термина существуют и другие значения, см. Производная. В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления. Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению. Рассмотрим функцию
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате. Связь с градиентом Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
где Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины Например, если взять в качестве
С математической точки зрения градиент — это производная скалярной функции, определенной на векторном пространстве. Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным. Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл. Стандартные обозначения: Определение Для случая трёхмерного пространства градиентом скалярной функции
Или, использовав для единичных векторов по осям прямоугольных декартовых координат
Если
компоненты которого равны частным производным · Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь. · Оператором градиента (обозначаемым обычно, как говорилось выше, grad или
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат
или, опуская по правилу Эйнштейна знак суммы,
(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах. Пусть Разбиение Мелкость разбиения
Разбиение называется конечным, если является конечным множеством, и измеримым, если все его элементы — измеримые (в данном случае — по Жордану) множества. Кратным (n-кратным) интегралом функции f на множестве B называется число I (если оно существует), такое что, какой бы малой
Здесь Это определение можно сформулировать в другой форме с использованием интегральных сумм. А именно, для данного разбиения
Кратным интегралом функции
если он существует. Предел берётся по множеству всех последовательностей разбиений, с мелкостью стремящейся к 0. Разумеется, это определение отличается от предыдущего, по сути, лишь используемым языком. Интеграл обозначается следующим образом: В векторном виде:
Геометрический смысл двойного интеграла Пусть функция f(x,y) принимает в области D только положительные значения. Тогда двойной интеграл численно равен объему V вертикального цилиндрического тела, построенного на основании D и ограниченного сверху соответствующим куском поверхности z=f(x,y).
24) Двойной интеграл [править]
Геометрический смысл двойного интеграла Двойным интегралом называют кратный интеграл с d=2.
В прямоугольных координатах: Геометрический смысл двойного интеграла [править] Пусть функция f(x,y) принимает в области D только положительные значения. Тогда двойной интеграл Выражение двойного интеграла через полярные координаты [править]
Переход из прямоугольных координат в полярные. В некоторых случаях двойной интеграл проще считать не в прямоугольных, а в полярных координатах, так как при этом может произойти существенное упрощение вида области интегрирования и всего процесса интегрирования в целом. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
Модуль якобиана отображения равен
Здесь 25) Тройные интегралы имеют те же свойства, что и двойные интегралы (линейность, аддитивность, формулы среднего значения и т.д.) I. Вычисление тройных интегралов с помощью повторного интегрирования. 1. Предположим, что функция f(x, y, z) непрерывна в рассматриваемой области T. Пусть сначала T = [a, b; c, d; e, f] - прямоугольный параллелепипед, проектирующийся на плоскость yz в прямоугольник R = [c, d; e, f]. Тогда
Заменяя в (1) двойной интеграл повторным, получим
Вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов. Если первые два интеграла в (2) объединить в двойной, то будем иметь
где P = [a, b; c, d] - проекция параллелепипеда T на плоскость xy. Заметим, что в этих случаях можно менять роли переменных. 2. Пусть область T заключена между плоскостями x = a и x = b, причём каждое сечение области T плоскостью
3. Пусть теперь тело T представляет собой "цилиндрический брус", ограниченный снизу и сверху, соответственно, поверхностями z = z1(x, y) и z = z2(x, y), проектирующиеся на плоскость xy в некоторую квадрируемую фигуру G (рис.2), z1(x, y) и z2(x, y) - непрерывны в G. Тогда
Если G = {(x, y): a
Отметим, что наряду с указанными формулами имеют место и им подобные, получающиеся перестановкой переменных x, y и z. II. Замена переменных в тройном интеграле
Если выполняются условия 26) Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).
Пусть M(x, y, z) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел
Якобиан отображения (8) 2. Сферические координаты. Пусть M(x, y) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно задаётся тройкой чисел
Они связаны с прямоугольными формулами
Якобиан отображения Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой
Переходя в этом равенстве к новым переменным по формулам (6), получим выражение объёма области T в криволинейных координатах
Пусть T - материальное тело (кубируемая область) с плотностью Тогда
Пример1. Вычислить объём тела, ограниченного поверхностями: x2 + y2 + z2 = a2, x2 + y2 - ax = 0. (рис. 5)
Решение. Рассмотрим одну четвёртую часть тела, лежащёю в первом октанте. Часть поверхности
Перейдём в интеграле к цилиндрическим координатам по формулам (8). При этом уравнение окружности x? + y? - ax = 0 преобразуется в кривую Таким образом
Пример 2. Вычислить интеграл
где T - область, ограниченная поверхностями Решение. Перейдём в интеграле к сферическим координатам по формулам (9). Тогда область интегрирования можно задать неравенствами
А, значит,
27) Криволинейный интеграл — интеграл, вычисляемый вдоль какой-либо кривой на плоскости или в пространстве. Утверждения в этой статье приведены для пространства Определения Пусть l — гладкая, без особых точек и самопересечений кривая (допускается одно самопересечение — случай замкнутой кривой), заданная параметрически.
Пусть Зададим разбиение кривой За Введем мелкость разбиения отрезка параметризации Введем набор промежуточных точек разбиения отрезка параметризации l: Зададим набор промежуточных точек разбиения кривой Пусть нам также даны 4 функции, которые определены вдоль кривой l:
Рассмотрим 4 интегральные суммы. 1. Интегральная сумма криволинейного интеграла первого рода:
1. Три интегральных суммы криволинейного интеграла второго рода:
Если Если
Сумму криволинейных интегралов второго рода функций P, Q и R также называют криволинейным интегралом второго рода вектор-функции
Если кривая L замкнута (начало совпадает с концом), то в этом случае вместо значка Свойства 1. Линейность:
2. Аддитивность: если
3. Монотонность: если
4. Теорема о среднем для непрерывной вдоль L функции f:
Очевидно, что: 5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: 6. Криволинейный интеграл первого рода не зависит от параметризации кривой. Вычисление Пусть l — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция
Здесь точкой обозначена производная по t: 28)Поверхностный интеграл второго рода[править] Определение[править] Рассмотрим двустороннюю поверхность Ф, гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации. Для определенности предположим сначала, что поверхность задана явным уравнением Пусть теперь в точках данной поверхности
Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от
распространенным на выбранную сторону поверхности Ф, и обозначают символом
(здесь dx dy) напоминает о площади проекции элемента поверхности на плоскость xy Если вместо плоскости xy спроектировать элементы поверхности на плоскость yz или zx, то получим два других поверхностных интеграла второго типа:
В приложениях чаще всего встречаются соединения интегралов всех этих видов:
где P,Q,R, суть функции от Связь между поверхностными интегралами второго и первого рода[править]
Свойства[править] 1. Линейность: 2. Аддитивность: 3. При изменении ориентации поверхности, поверхностный интеграл меняет знак. 29) Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля пообъёму, ограниченному этой поверхностью:
то есть интеграл от дивергенции векторного поля F, распространённый по некоторому объёму V, равен потоку вектора через поверхность S, ограничивающую данный объём. Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности. В работе Остроградского формула записана в следующем виде:
где w и s — дифференциалы объёма и поверхности соответственно. В современной записи 30) Теорема Стокса — одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса. Формула Кельвина — Стокса Пусть
или в координатной записи:
|
|||||||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.104.65 (0.011 с.) |

 от n аргументов в окрестности точки
от n аргументов в окрестности точки  . Для любого единичного вектора
. Для любого единичного вектора 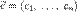 определим производную функции f в точке
определим производную функции f в точке 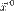 по направлению
по направлению 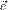 следующим образом:
следующим образом: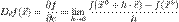
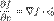 ,
,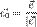 — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора
— орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора  .
. , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.
, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении. высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.
высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.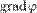 или, с использованием оператора набла,
или, с использованием оператора набла, 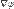 — вместо
— вместо  может быть любое скалярное поле, обозначенное любой буквой, например
может быть любое скалярное поле, обозначенное любой буквой, например 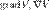 — обозначения градиента поля V.
— обозначения градиента поля V.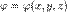 координат x, y, z называется векторная функция с компонентами
координат x, y, z называется векторная функция с компонентами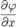 ,
, 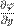 ,
, 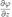 .
.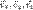 :
: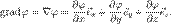
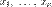 , то её градиентом называется n-мерный вектор
, то её градиентом называется n-мерный вектор
 по всем её аргументам.
по всем её аргументам. ) называется оператор, действие которого на скалярную функцию (поле) дает ее градиент. Этот оператор иногда коротко называют просто "градиентом".
) называется оператор, действие которого на скалярную функцию (поле) дает ее градиент. Этот оператор иногда коротко называют просто "градиентом".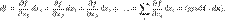
 , то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку dx — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:
, то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку dx — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как: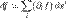
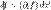
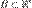 — измеримое[1] множество n-мерного вещественного пространства,
— измеримое[1] множество n-мерного вещественного пространства, 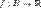 — функция на B.
— функция на B. множества B — это набор попарно непересекающихся подмножеств
множества B — это набор попарно непересекающихся подмножеств 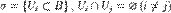 , такое что
, такое что 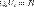 .
.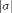 — это наибольший диаметр множеств
— это наибольший диаметр множеств 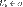 .
.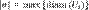
 -окрестностью числа I мы ни задались, всегда найдется такое разбиение множества B и набор промежуточных точек, что сумма произведений значения функции в промежуточной точке разбиения на меру разбиения будет попадать в эту окрестность. Формально:
-окрестностью числа I мы ни задались, всегда найдется такое разбиение множества B и набор промежуточных точек, что сумма произведений значения функции в промежуточной точке разбиения на меру разбиения будет попадать в эту окрестность. Формально: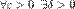 :
: 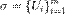 :
: 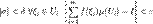
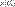 — мера множества
— мера множества  .
.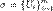 и множества точек
и множества точек 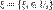 рассмотрим интегральную сумму
рассмотрим интегральную сумму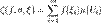
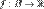 называют предел
называют предел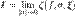
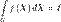 ,Либо ставят значок интеграла d раз, записывают функцию и d дифференциалов:
,Либо ставят значок интеграла d раз, записывают функцию и d дифференциалов: 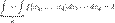 .Для двойного и тройного интегралов используются также обозначения
.Для двойного и тройного интегралов используются также обозначения 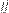 и
и 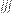 соответственно.В современных математических и физических статьях многократное использование знака интеграла не применяется.Такой кратный интеграл называется интегралом в собственном смысле.В случае n=1 кратный интеграл совпадает с интегралом Римана.Свойства кратных интегралов.Линейность по функции. Пусть G измеримо, функции f и g интегрируемы на G, тогда
соответственно.В современных математических и физических статьях многократное использование знака интеграла не применяется.Такой кратный интеграл называется интегралом в собственном смысле.В случае n=1 кратный интеграл совпадает с интегралом Римана.Свойства кратных интегралов.Линейность по функции. Пусть G измеримо, функции f и g интегрируемы на G, тогда 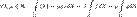 .Аддитивность по множеству интегрирования. Пусть множества
.Аддитивность по множеству интегрирования. Пусть множества 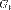 и
и 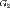 измеримы,
измеримы, 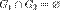 и
и 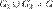 . Пусть также функция f(X)определена и интегрируема на каждом из множеств G1 и G2. Тогда интеграл по G существует и равен
. Пусть также функция f(X)определена и интегрируема на каждом из множеств G1 и G2. Тогда интеграл по G существует и равен 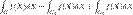 .Монотонность по функции. Пусть G измеримо, функции f и g интегрируемы на G, причем
.Монотонность по функции. Пусть G измеримо, функции f и g интегрируемы на G, причем 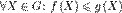 . Тогда
. Тогда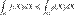 .Интегральное неравенство треугольника. Следствие предыдущего свойства.
.Интегральное неравенство треугольника. Следствие предыдущего свойства. 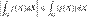 Интегральная теорема о среднем. Пусть G — компакт, функция f(X) непрерывна и интегрируема на G, тогда
Интегральная теорема о среднем. Пусть G — компакт, функция f(X) непрерывна и интегрируема на G, тогда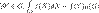 Постоянная функция f(X)=c интегрируема на любом измеримом множестве G, причем
Постоянная функция f(X)=c интегрируема на любом измеримом множестве G, причем 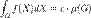 .Как следствие,
.Как следствие, 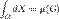 .
.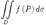 . Здесь
. Здесь 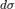 — элемент площади в рассматриваемых координатах.
— элемент площади в рассматриваемых координатах.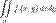 , где dxdy — элемент площади в прямоугольных координатах.
, где dxdy — элемент площади в прямоугольных координатах.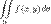 численно равен объему V вертикального цилиндрического тела, построенного на основании D и ограниченного сверху соответствующим куском поверхности
численно равен объему V вертикального цилиндрического тела, построенного на основании D и ограниченного сверху соответствующим куском поверхности 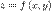 .
. Переход из прямоугольных координат в полярные.
Переход из прямоугольных координат в полярные. 
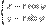
 . Таким образом получаем, что
. Таким образом получаем, что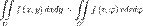 .
.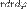 является элементом площади в полярных координатах.
является элементом площади в полярных координатах.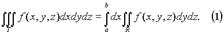
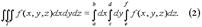
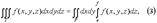
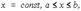 представляет собой квадрируемую фигуру G(x)(рис. 1). Тогда
представляет собой квадрируемую фигуру G(x)(рис. 1). Тогда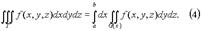
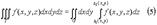
 x
x 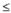 b, y1(x)
b, y1(x)  y
y 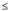 y2(x)}, то
y2(x)}, то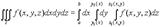
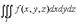 состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам
состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам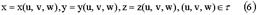
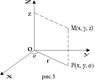
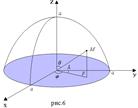
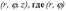 - полярные координаты точки P, z - аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид
- полярные координаты точки P, z - аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид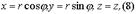
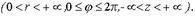
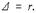
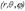 , где r - расстояние точки M до точки 0,
, где r - расстояние точки M до точки 0, 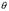 - угол между лучами OM и OZ,
- угол между лучами OM и OZ, 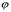 - полярный угол точки P на плоскости xy. Тройка чисел
- полярный угол точки P на плоскости xy. Тройка чисел 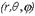 называется сферическими координатами точки M.
называется сферическими координатами точки M.
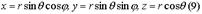
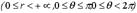
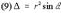 . Иногда используются обобщённые сферические координаты.
. Иногда используются обобщённые сферические координаты.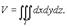
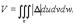
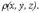
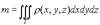 - масса тела.
- масса тела.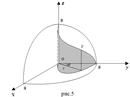
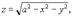 вырезанная цилиндром, проектируется в область
вырезанная цилиндром, проектируется в область 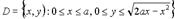 . Тогда
. Тогда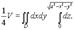
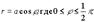 а уравнение поверхности
а уравнение поверхности 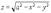 - к виду
- к виду 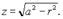
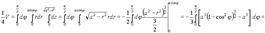
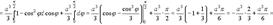
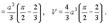
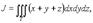

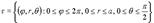
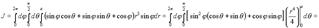
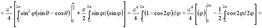
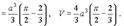
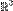 , но могут быть обобщены на пространство произвольной размерности.
, но могут быть обобщены на пространство произвольной размерности.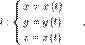
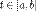 — (отрезок параметризации) — рассматриваем часть кривой.
— (отрезок параметризации) — рассматриваем часть кривой. — разбиение отрезка параметризации
— разбиение отрезка параметризации 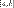 , причем
, причем 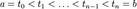 .
.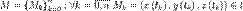 .
.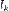 обозначим часть кривой от точки
обозначим часть кривой от точки 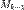 до точки
до точки 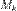 ,
, 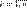 .
. :
: 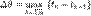 .
.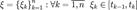 .
. .
.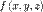 ,
, 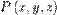 ,
, 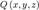 ,
,  .
.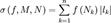 .
.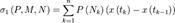 ,
,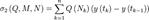 ,
,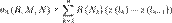 .
.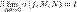 , то говорят, что функция f интегрируема в смысле криволинейного интеграла первого рода по кривой l, а сам предел называют криволинейным интегралом первого рода функции f по кривой l и обозначают
, то говорят, что функция f интегрируема в смысле криволинейного интеграла первого рода по кривой l, а сам предел называют криволинейным интегралом первого рода функции f по кривой l и обозначают 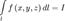 . Здесь dl — дифференциал кривой.
. Здесь dl — дифференциал кривой.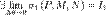 ,
, 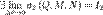 ,
, 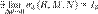 , то говорят, что функции P, Q и R интегрируемы в смысле криволинейного интеграла второго рода по кривой l, а сами пределы называют криволинейными интегралами второго рода функций P, Q и R по кривой l и обозначают
, то говорят, что функции P, Q и R интегрируемы в смысле криволинейного интеграла второго рода по кривой l, а сами пределы называют криволинейными интегралами второго рода функций P, Q и R по кривой l и обозначают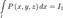
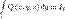
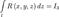
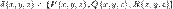 и обозначают:
и обозначают: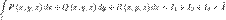 .
.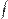 принято писать
принято писать  .
.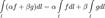
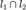 в одной точке, то
в одной точке, то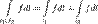
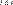 на
на 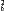 , то
, то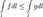

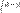 .
.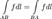 .
. определена и интегрируема вдоль кривой l в смысле криволинейного интеграла первого рода. Тогда
определена и интегрируема вдоль кривой l в смысле криволинейного интеграла первого рода. Тогда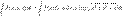 .
.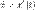 .
.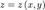 причем точка
причем точка 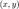 изменяется в области
изменяется в области 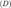 на плоскости
на плоскости  , ограниченный кусочно-гладким контуром.
, ограниченный кусочно-гладким контуром. определена некоторая функция
определена некоторая функция 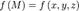 . Разбив поверхность сетью кусочно-гладких кривых на части
. Разбив поверхность сетью кусочно-гладких кривых на части  и выбрав на каждой такой части точку
и выбрав на каждой такой части точку 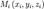 вычисляем значение функции
вычисляем значение функции 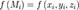 в данной точке и умножим его на площадь
в данной точке и умножим его на площадь 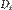 проекции на плоскость x y элемента
проекции на плоскость x y элемента 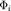 , снабженную определенным знаком. Составим интегральную сумму:
, снабженную определенным знаком. Составим интегральную сумму: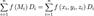 .
.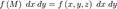 ,
,
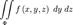 или
или 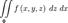 .
.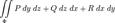
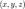 , определенные в точках поверхности
, определенные в точках поверхности 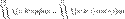 , где v — единичный вектор нормали поверхности
, где v — единичный вектор нормали поверхности  ,
, 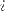 — орт.
— орт. ;
;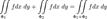 ;
;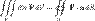
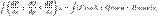
 — элемент объёма, s=dS — элемент поверхности.
— элемент объёма, s=dS — элемент поверхности.  — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.
— функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью. — кусочно-гладкая поверхность (
— кусочно-гладкая поверхность (  ) в трёхмерном евклидовом пространстве (n=3), F — дифференцируемое векторное поле. Тогда циркуляция векторного поля вдоль замкнутого контура
) в трёхмерном евклидовом пространстве (n=3), F — дифференцируемое векторное поле. Тогда циркуляция векторного поля вдоль замкнутого контура 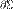 равна потоку ротора (вихря) поля через поверхность
равна потоку ротора (вихря) поля через поверхность  , ограниченную контуром:
, ограниченную контуром: