Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормы опасных и мешающих напряженийСодержание книги
Поиск на нашем сайте
6. Расчет мешающих влияний
Форма кривой тока в тяговой сети электрических железных дорог переменного тока значительно искажается из-за наличия выпрямительных агрегатов на электровозах однофазно-постоянного тока. Поэтому ток тяговой сети содержит нечетные гармонические составляющие тональных и высших частот, которые индуктируют в линии связи электродвижущие силы соответствующих частот. Вследствие этого в телефонных цепях в силу продольной и поперечной несимметрии проводов связи появляются напряжения, которые накладываются на полезные сигналы и вызывают шумы, снижающие качество передачи разговора, а в телеграфных цепях появляются токи, искажающие передаваемые сигналы. Такие влияния, которые нарушают нормальное действие связи, называют мешающими. Мешающее действие наведенного в линии связи напряжения оценивается напряжением шума UШ. Напряжения, индуцируемые в двухпроводной линии связи под действием электромагнитных полей тяговой сети, обусловлены асимметричным расположением проводов телефонной цепи линии связи по отношению к проводам тяговой сети, а также асимметрией проводов линии связи по отношению к земле. Напряжения различной частоты из-за особенностей человеческого слуха создают в линиях связи неодинаковые помехи. Поэтому индуктированные разными гармониками напряжения приводят к псофометрическому, т. е. к частоте 800 Гц при помощи коэффициента акустического воздействия рk (k – порядковой номер гармоники), учитывающего относительное мешающее воздействие напряжений различной частоты. В двухпроводных линиях связи индуктируется электродвижущая сила в обоих проводах. Вследствие того, что любая реальная двухпроводная линия имеет продольную и поперечную асимметрию, т. е. неодинаковые электрические параметры проводов по длине линии, в конце линии возникает результирующее напряжение помехи, которое будет тем больше, чем больше асимметрия /3/. Качество двухпроводной линии связи оценивается коэффициентом чувствительности hk к помехам от каждой гармоники с номером k. Этот коэффициент представляет собой отношение напряжения помехи в конце линии к среднему значению напряжений на концах обоих проводов относительно земли. Частотные зависимости hk для отдельных линий приведены в таблице 2.4.
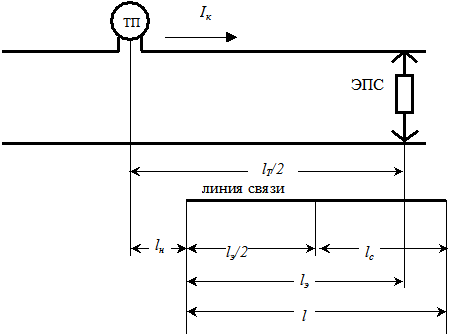
Для двухпроводных телефонных цепей псофометрическое значение мешающего напряжения определяют при нормальном режиме работы тяговой сети. При вычислении величины мешающего напряжения в телефонных цепях, в качестве влияющих следует принимать все тяговые плечи в пределах расчетного участка, полагая, что тяговая сеть состоит из плеч одностороннего питания. Применительно к настоящей курсовой работе величину мешающего напряжения следует вычислять для случая, когда влияющий электровоз находится возле поста секционирования, расположенного в середине фидерной зоны, слева от него. При этом пост отключен (рис. 6.1). Кривая тока, потребляемая электровозом, задана в Приложении. В технике исследования влияний применяется метод гармонического анализа влияющих кривых токов и напряжений, когда каждая влияющая кривая представляется спектром. Задача определения величины напряжения шума состоит в расчете наведенных напряжений от каждой гармонической составляющей (как от генератора, работающего на частоте гармоники) на основе принципа наложения и дальнейшим определением суммарной помехи в линии связи, учитывая при этом законы распространения токов и напряжений в тяговой сети и в линии связи, как в линиях с распределенными параметрами.
Рис. 6.1. Схема для расчета мешающего влияния тяговой сети Таким образом, при спектральном методе исследования ток тяговой сети представляют спектром гармонических составляющих, определяют напряжение шума UШk в линии связи от каждой гармоники тягового тока, а затем определяют общее напряжение шума в линии связи как среднеквадратичное значение напряжений шума отдельных гармоник. Согласно «Правилам защиты устройств проводной связи проводного вещания от влияния тяговой сети электрических железных дорог переменного тока» величина напряжения шума в двухпроводных телефонных цепях может быть вычислена по формуле:
Применительно к настоящей курсовой работе величину мешающего напряжения следует вычислять по формуле:
Величину мешающего напряжения
Отдельные величины, входящие в эту формулу:
где
где
Расчетные длины Если пренебречь возможными резонансными явлениями в тяговой сети, то токи отдельных гармонических составляющих можно принять равными гармоническим составляющим тока электровоза и определить по заданной кривой любым известным графоаналитическим методом. Один из простейших таких методов (численное интегрирование) состоит в замене интегралов, определяющих синусную
если Графоаналитический метод гармонического анализа несинусоидального тока или напряжения заключается в том, что по снятой осциллограмме определяют состав и порядок гармонических составляющих, их амплитуду и начальную фазу по отношению к исследуемой кривой или к основной гармонике. Можно таким же образом определить амплитудное и действующее значение несинусоидальной величины, а также коэффициенты искажений, несинусоидальности и другие синусоидальные функции. Графический метод определения гармоник ряда Фурье основан на замене определенного интеграла суммой конечного числа слагаемых. С этой целью период функции
и интегралы заменяют суммами. По определению постоянная составляющая:
или
где
Амплитуда синусной составляющей
или
Амплитуда косинусной составляющей k-й гармоники:
Здесь При расчетах по формулам (6.8) – (6.12) обычно достаточно разделить период на Перед тем как производить графическое разложение в ряд, необходимо выяснить, не обладает ли раскладываемая функция симметрией относительно осей координат /4/. Наличие того или иного вида симметрии позволяет до проведения разложения предсказать, какие гармоники следует ожидать. Так, если кривая Знак углов Так, например, если некоторый отрезок по оси абсцисс для первой гармоники выражает собой угол Пример. Найти первую и третью гармоники функции Таблица 6.1 Исходные данные для примера
p f(x) 13,5 15,4 17,4 20,5 25,4 32,5 27,7 19,2
Рис. 6.2. Несинусоидальная кривая
Решение. Так как кривая симметрична относительно оси абсцисс, то Амплитуда синусной составляющей первой гармоники:
Амплитуда косинусной составляющей первой гармоники:
Амплитуда синусной составляющей третьей гармоники:
Амплитуда косинусной составляющей третьей гармоники:
Амплитуда первой гармоники:
Тангенс угла
Амплитуда третьей гармоники:
Следовательно, если ограничиться третьей гармоникой, то:
На рис. 6.3 изображены первая и третья гармоники полученного ряда, а также результирующая (суммарная) кривая. Ее можно сопоставить с кривой на рис. 6.2.
Для того чтобы получить значения коэффициентов
Рис. 6.3. Разложение несинусоидальной кривой на гармоники
Допускаемые опасные напряжения для режима короткого замыкания и вынужденного режима имеют различные значения. Для режима короткого замыкания допустимые напряжения зависят от времени отключения короткого замыкания и составляют для воздушной линии с железобетонными опорами: при tоткл = 0,1 с Uдоп = 500 В; при tоткл = 0,15 с Uдоп = 450 В; при tоткл = 0,30 с Uдоп = 310 В; при tоткл = 0,60 с Uдоп = 160 В. Для воздушной линии с железобетонными опорами при вынужденном режиме работы допустимое напряжение составляет 36 В. При выполнении работы следует принять tоткл = 0,15 с. Нормы мешающего напряжения зависят от назначения цепи связи. При выполнении курсовой работы следует ориентироваться на величину 1,5 мВ.
|
||||||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.201.192 (0.012 с.) |

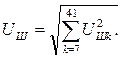 (6.1)
(6.1)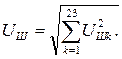 (6.2)
(6.2)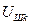 в мВ для k-й гармоники в телефонных цепях тональной частоты вычисляют по формуле:
в мВ для k-й гармоники в телефонных цепях тональной частоты вычисляют по формуле: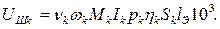 (6.3)
(6.3)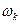 – угловая частота k-й гармонической составляющей, рад/с;
– угловая частота k-й гармонической составляющей, рад/с;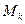 – взаимная индуктивность между контактным проводом и проводом связи для k-й гармонической составляющей, Гн/км. Эта величина может быть определена по формуле (4.4);
– взаимная индуктивность между контактным проводом и проводом связи для k-й гармонической составляющей, Гн/км. Эта величина может быть определена по формуле (4.4);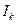 – ток k-й гармонической составляющей в тяговой сети, А;
– ток k-й гармонической составляющей в тяговой сети, А;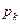 – коэффициент акустического воздействия для k-й гармонической составляющей влияющего тока;
– коэффициент акустического воздействия для k-й гармонической составляющей влияющего тока;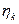 – коэффициент чувствительности двухпроводной цепи для k-й гармонической составляющей влияющего тока;
– коэффициент чувствительности двухпроводной цепи для k-й гармонической составляющей влияющего тока;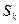 – результирующий коэффициент экранирующего действия для k-й гармонической составляющей:
– результирующий коэффициент экранирующего действия для k-й гармонической составляющей: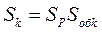 , (6.4)
, (6.4)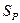 – коэффициент экранирования рельсов (значения этого коэффициента приведены выше);
– коэффициент экранирования рельсов (значения этого коэффициента приведены выше);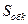 – коэффициент экранирующего действия оболочки кабеля для k-й гармонической составляющей (значения его приведены в таблице 2.5);
– коэффициент экранирующего действия оболочки кабеля для k-й гармонической составляющей (значения его приведены в таблице 2.5);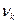 – коэффициент, характеризующий волновые процессы в линии связи для k-й гармонической составляющей, при этом:
– коэффициент, характеризующий волновые процессы в линии связи для k-й гармонической составляющей, при этом: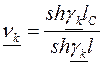 , (6.5)
, (6.5)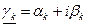 – постоянная распространения однопроводной цепи, подверженной влиянию для k-й гармонической составляющей. Величина a характеризует изменение амплитуды напряжения вдоль линии, а b – изменение фазового угла. В формулу (6.5) следует подставлять модули значений гиперболических функций. При этом следует помнить, что эти функции берутся от комплексного аргумента. Определение гиперболического синуса от комплексного аргумента может быть произведено по формуле:
– постоянная распространения однопроводной цепи, подверженной влиянию для k-й гармонической составляющей. Величина a характеризует изменение амплитуды напряжения вдоль линии, а b – изменение фазового угла. В формулу (6.5) следует подставлять модули значений гиперболических функций. При этом следует помнить, что эти функции берутся от комплексного аргумента. Определение гиперболического синуса от комплексного аргумента может быть произведено по формуле: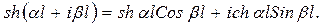 (6.6)
(6.6)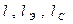 – см. рис. 6.1.
– см. рис. 6.1.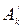 и косинусную
и косинусную 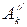 составляющие (вторая форма ряда Фурье) соответствующими суммами. Взаимное расположение отдельных гармоник относительно друг друга при расчете напряжения шумазначения не имеет, а величина k-й гармонической в кривой тока будет равна
составляющие (вторая форма ряда Фурье) соответствующими суммами. Взаимное расположение отдельных гармоник относительно друг друга при расчете напряжения шумазначения не имеет, а величина k-й гармонической в кривой тока будет равна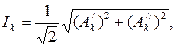 (6.7)
(6.7)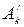 и
и 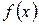 , равной 2
, равной 2 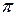 , разбивают на n равных частей
, разбивают на n равных частей 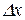 :
: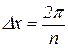 ,
,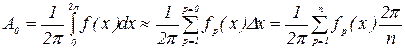 (6.8)
(6.8)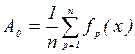 , (6.9)
, (6.9)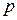 – текущий индекс; он пробегает значения от 1 до
– текущий индекс; он пробегает значения от 1 до 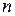 ;
;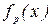 – значение функции
– значение функции 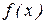 при
при 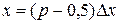 , т. е. в середине
, т. е. в середине  k-й гармоники ряда
k-й гармоники ряда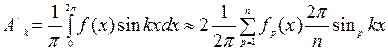 (6.10)
(6.10)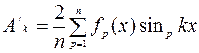 (6.11)
(6.11) . (6.12)
. (6.12)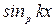 и
и 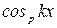 – соответственно значения функции
– соответственно значения функции 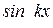 и
и 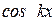 при
при 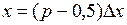 , т. е. в середине
, т. е. в середине 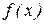 симметрична относительно абсцисс, то постоянная составляющая
симметрична относительно абсцисс, то постоянная составляющая 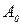 и все четные гармоники отсутствуют, а вычисляя
и все четные гармоники отсутствуют, а вычисляя 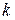 , следует учесть, что сумма
, следует учесть, что сумма 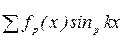 за первый полупериод равна сумме
за первый полупериод равна сумме 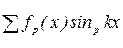 за второй полупериод.
за второй полупериод.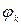 зависит от знаков
зависит от знаков 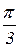 , то тот же отрезок для третьей гармоники выражает собой угол, в 3 раза больший, т. е.
, то тот же отрезок для третьей гармоники выражает собой угол, в 3 раза больший, т. е. 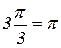 .
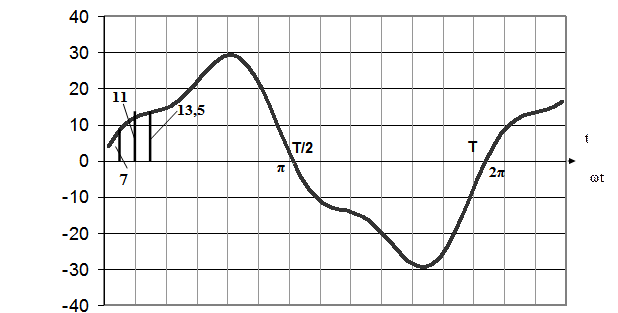
.
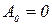 и ряд будет состоять только из нечетных гармоник.
и ряд будет состоять только из нечетных гармоник.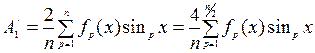 ,
,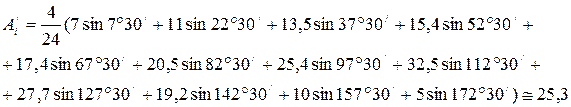
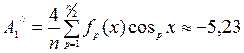 .
.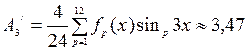 .
.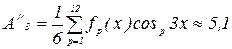 .
.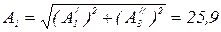 .
.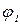 , на который начало первой гармоники смещено по отношению к началу кривой
, на который начало первой гармоники смещено по отношению к началу кривой 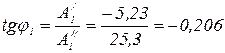 ,
,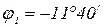 .
.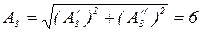 ,
,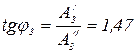 ;
; 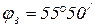 .
.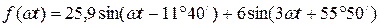 .
.