Задачи для самостоятельного решения

Коэф.

Y(х)

a

b

c

d

a+bx

1,800

0,636

 

 

a+bx+cx2

4,050

–0,489

0,102

 

a+bx+cx2+dx3

–2,033

4,907

–1,067

0,071

П о г р е

ш н о с

т и

Аргумент X

Функция

Y(Х)

Прямая

Пара-

бола

3-я

степень

1,00

2,063

7,095

0,769

5,00

3,714

2,305

0,851

6,00

5,248

6,227

1,013

5,00

0,428

1,608

0,003

4,00

0,964

0,027

0,455

3,00

6,855

3,240

1,663

4,00

5,083

2,693

0,104

6,00

0,794

0,471

0,644

9,00

2,169

1,131

2,753

10,00

3,372

0,371

1,387

Сумма квадратов:

30,691

25,168

9,641

Рис.3-1

В общем случае это выражение вида

(<Функция Y(x)> – <Функция регрессии>)2.

Для уравнения первого порядка (прямой)

(<Функция Y(x)> – (a+b(x))2.

Таким образом, для первой клетки погрешности

Прямой: C8=($B8–($B$3+$C$3*$A8))^2.

Аналогичные формулы заносятся (копируются) во все нижележащие клетки (область С9:С17). В клетке С18 вычисляется сумма погрешностей для всех точек С18=СУММ(С8:С17).

Нашей целью является приведение этой погрешности к минимуму путем изменения значений коэффициентов уравнения прямой (клеток В3 и С3). В исходном состоянии они пустые.

Для поиска оптимальных значений в окне Поиск решения в качестве целевой ячейки следует установить клетку С18, а в качестве изменяемых параметров – область В3:С3 (рис. 3-2). Результаты, полученные в изменяемых ячейках, соответствуют уравнению вида y=1,8+0,6364x.Общая погрешность приближения (клетка С18) составила 30,69.

Поиск решения

Установить целевую ячейку

$C$18

 

Равной: š максимальному значению

           ž минимальному значению

Изменяя ячейки:––––––––––––––––

$B$3:$C$

Рис.3-2

Аналогичным образом заполняется столбец D8:D18 погрешностей для полинома второй степени (параболы).

Здесь D8=($B8–($B$4+$C$4*$A8+$D$4*$A8^2))^2.

В окне Поиск решения целевая ячейка – D18, изменяемые параметры – область В4:D4. Полученный результат соответствует уравнению

y = 4,05 – 0,4886x + 0,1023x2.

Аналогично для уравнения третьей степени

E8=($B8–($B$5+$C$5*$A8+$D$5*$A8^2+$E$5*A8^3))^2.

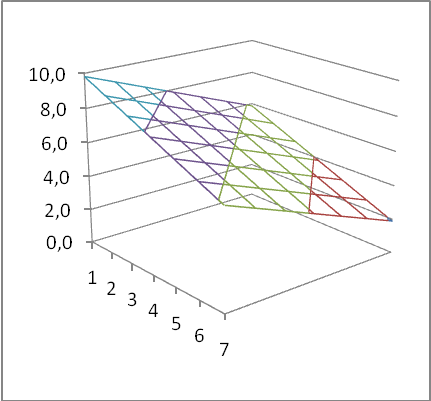
Рис.3-3

В окне Поиск решения целевая ячейка – E18, изменяемые параметры – область B4:E5. Результат описывается уравнением

y= – 2,0333 + 4,907x – 1,0676x2 + 0,0709x3.

Точно так же (в таблице не показано) может быть сформировано уравнение четвертой степени

y=–10,083 + 15,227x – 4,844x2 + 0,5869x3 – 0,0235x4.

С повышением порядка уравнения регрессии погрешность приближения все время уменьшается

30,6909 Þ 25,1682 Þ 9,6408 Þ 0,5775.

Графическое отображение результатов вычислений приведено на рис. 3-3 (исходные точки обозначены прямоугольниками). Оно подтверждает этот вывод – линии уравнений более высокой степени находятся ближе к исследуемым точкам.

Увеличение степени аппроксимирующего полинома снижает погрешность. Самая высокая возможная степень такого уравнения на единицу меньше числа точек (в рассмотренном примере теоретически возможен полином девятой степени). При этом аппроксимирующая кривая пройдет в точности через все наши точки. На практике, однако, нет необходимости стремиться к полному устранению погрешности, поскольку и сами данные никогда не являются точными. Наоборот, нужно стараться, конечно, без потери качества, ограничиться как можно меньшей степенью кривой.

Применение описанной методики позволяет в качестве уравнения регрессии использовать не только степенные полиномы, но и другие функции.

Отметим, что средства деловой графики позволяют найти уравнения регрессии (до 6 степени включительно) и не прибегая к вычислениям. Если, после того как была построена кривая функции Y(X), щелкнуть на ней правой кнопкой мыши, в появившемся контекстном меню можно выбрать пункт Добавить линию тренда, который предъявляет окно Формат линия тренда. Здесь  можно выбрать вид уравнения аппроксимации и его степень, а если установить флаг Показывать уравнение на диаграмме, то на графике мы увидим не только линию тренда, но и его уравнение. Здесь же можно визуально оценить поведение анализируемого процесса в будущем/прошлом, если установить Прогноз вперед/назадна заданное число единиц независимого аргумента Х. К сожалению, предъявляемая функция отображается как текст, и не может быть непосредственно использована в вычислениях.

X

Y1

Y2

Y3

Y4

Y5

Y6

Y7

Y8

Y9

Y10

Y11

Y12

Справа приведена таблица из двенадцати вариантов функций Y(X). Для каждой из них известны восемь точек. Для своего варианта сделать следующее:

· Найти уравнения регрессии первой, второй и третьей степени, используя технологию, рассмотренную на рис. 3-1.

· Для Х=10 вычислить значение Y по этим уравнениям.

· Построить их кривые, аналогичные рис. 3-3.

· Построить аппроксимирующие зависимости, используя только средства деловой графики Excel.

4. Множественная линейная регрессия. Ранее нами была рассмотрена технология нахождения парной линейной регрессии Y(X). На практике, конечно, на исследуемую систему влияет не один, а несколько (или даже много) параметров. В этом случае необходимо использовать уже множественную регрессию, т.е. найти функцию вида Y(X,Z, …). Геометрическим представлением тогда будет не прямая линия, а плоскость или гиперплоскость.

Найдем сейчас коэффициенты уравнения линейной регрессии, для двух влияющих переменных Y(X,Z). Такое уравнение будет выглядеть так Y=a+bX+cZ. Таким образом, нам нужно найти три коэффициента А, В и С.

Поступим уже известным нам образом. Искомые коэффициенты будем искать (рис. 4-1) в клетках A2, B2, C2. Первоначально они пусты (т.е. коэффициенты a, b, c пока считаем равными нулю). В столбцы A, B, C (область A4:C10) внесем известные нам значения X, Y, Z. В столбец D внесем формулы для вычисления значений, полученных с помощью пока не найденной функции линейной регрессии Yл (D4=A$2+B$2*A4+C$2*B4). В клетку D11 – формулу (=СУММКВРАЗН(C4:C10;D4:D10)) суммирующую квадраты разностей двух векторов (у нас Y и Yл). Теперь вызываем Поиск решения, где задаем: установить в ячейке D11 минимальное значение, изменяя ячейки A2:C2. Результат мы видим в таблице – искомая функция такова Yл=9,8-0,7X-0,7Z.

Теперь построим диаграмму (рис. 4-2), отображающую наше решение. Она будет использовать данные из области G3:M6. Создадим ее. В столбец F внесем значения X, в строку 2 – значения Z. Клетки заполним формулами вычисляющими Yл для значений X и Z, на пересечении которых она находится (G3=$A$2+$B$2*$F3+$C$2*G$2).Затем строим диаграмму (Поверхность (проволочная)) из данных, находящихся в области G3:M6.

Уравнение множественной регрессии можно получить и, используя один из прилагаемых к Excel, дополнительных модулей –  Пакет анализа. С его помощью можно получить коэффициенты уравнения и его статистические характеристики.

 

A

B

C

D

E

F

G

H

I

J

K

L

Рис. 4-2

 

M

a

b

c

9,8

-0,7

-0,7

x\z

X

Z

Y

Yл

9,8

9,2

8,5

7,8

7,2

6,5

5,9

9,8

9,2

8,5

7,8

7,2

6,5

5,9

5,2

8,5

8,5

7,8

7,2

6,5

5,9

5,2

4,5

7,2

7,8

7,2

6,5

5,9

5,2

4,5

3,9

5,9

7,2

6,5

5,9

5,2

4,5

3,9

3,2

4,5

6,5

5,9

5,2

4,5

3,9

3,2

2,6

3,2

5,9

5,2

4,5

3,9

3,2

2,6

1,9

1,9

Сумма D²:

2,0

Рис.

4-1