Деление на двух- и трехзначные числа.

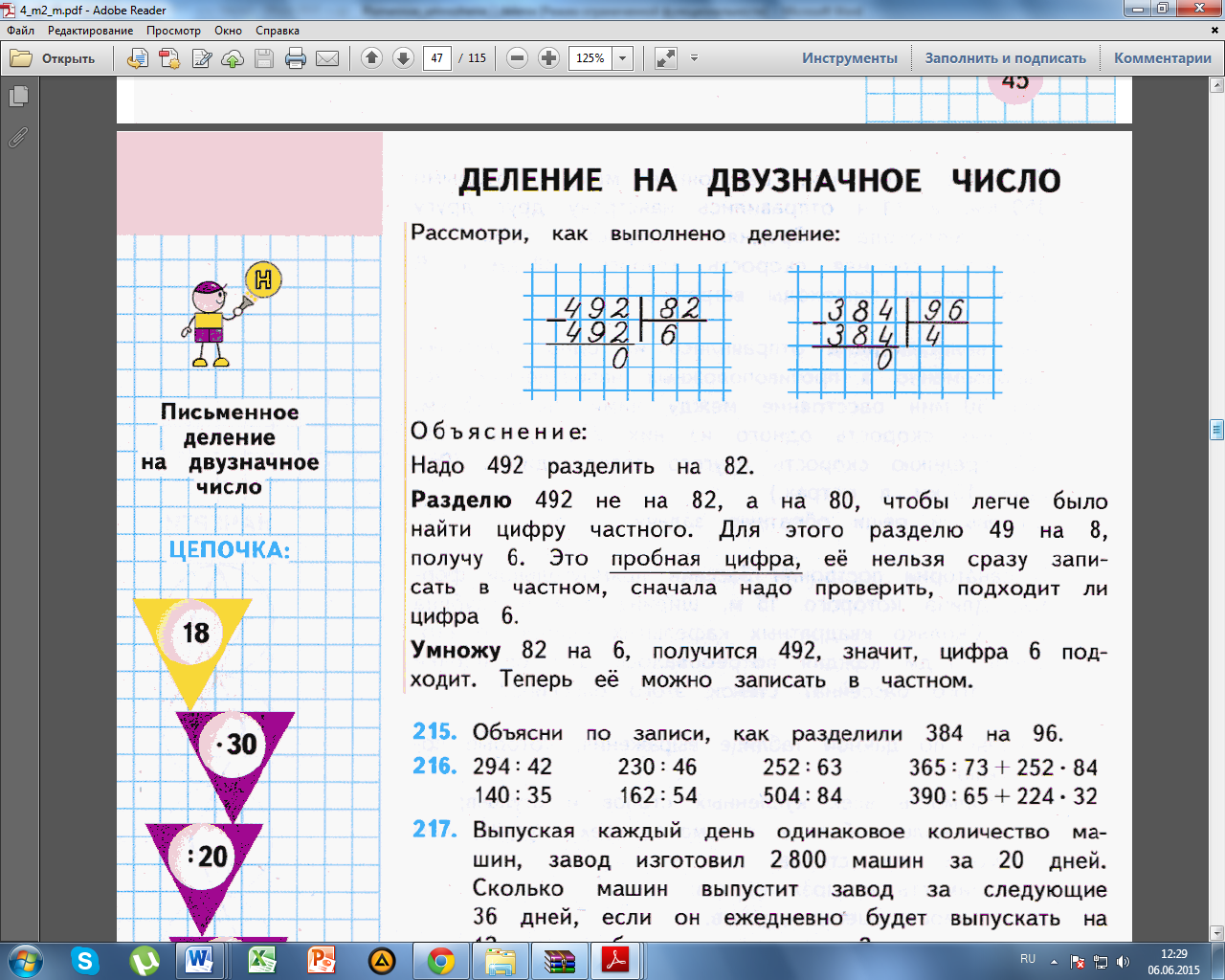
Задание 10

В чем сложность приема письменного деления на двух и трехзначные числа? Укажите последовательность изучения частных случаев деления, которые рассматриваются в учебниках математики начальных классов при знакомстве учащихся с алгоритмом письменного деления на двух и трехзначное число. Приведите рассуждения учеников в каждом из названных случаев.

Случаи деления, как и при освоении умножения, предъявляются по мере усложнения. Успешность освоение алгоритмов деления на двузначные и трехзначные числа зависит от того, насколько хорошо освоен алгоритм деления на однозначное число.

Перед тем, как начать изучать новый прием, дети должны повторить теоретическую основу. Теоретическую основу повторяют на подготовительном этапе.

ТО:

1) алгоритм письменного деления на однозначное и круглое число;

2) алгоритм письменного вычитания;

3) свойство деления суммы на число.

Затем на специальном уроке знакомят с приёмом деления на двухзначное число.

Для этого используют тот же алгоритм, что на 1 и 2 этапах, но в процессе рассуждения меняется этап подбора цифры частного.

Он усложняется, т.к. делят, например, на 82 и в уме это сделать очень сложно (это и есть ответ на вопрос «В чем сложность приема письменного деления на двух- и трехзначные числа»), поэтому округляют 82 до 80 и сначала делят на 10, потом на 8. Цифру частного называют пробной цифрой.

Программа М.И. Моро

По программе М.И. Моро данную тему начинают изучать в 4 классе. Рассмотрим поподробнее.

Сначала разбирают наиболее простые случаи, когда:

1. В частном получается однозначное число, причем число проб равно 1, т.е. пробная цифра сразу подходит.

М4М, ч.2, стр. 57

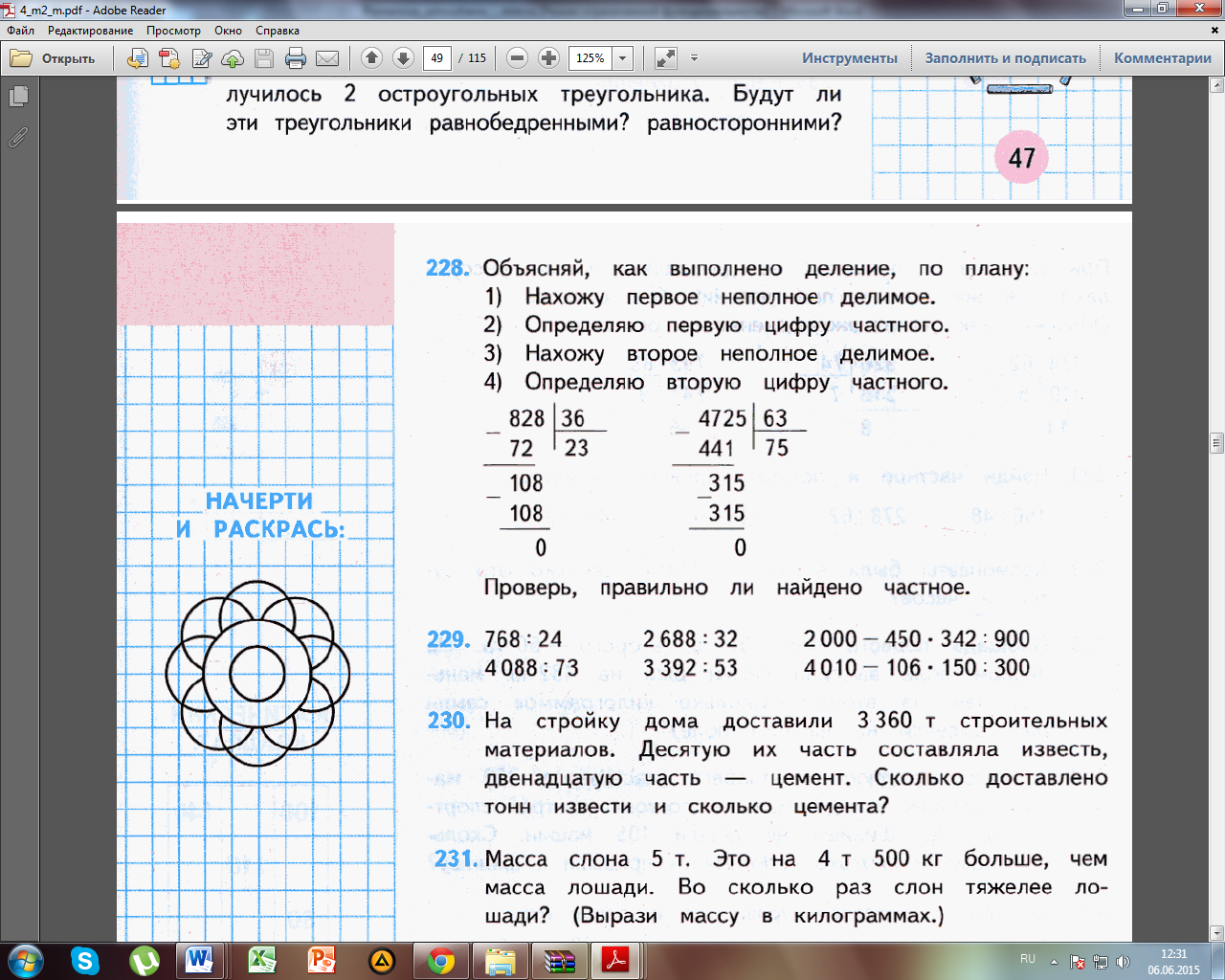
2. В частном получаем двузначное число, но число проб равно 1.

М4М, ч.2, стр. 59

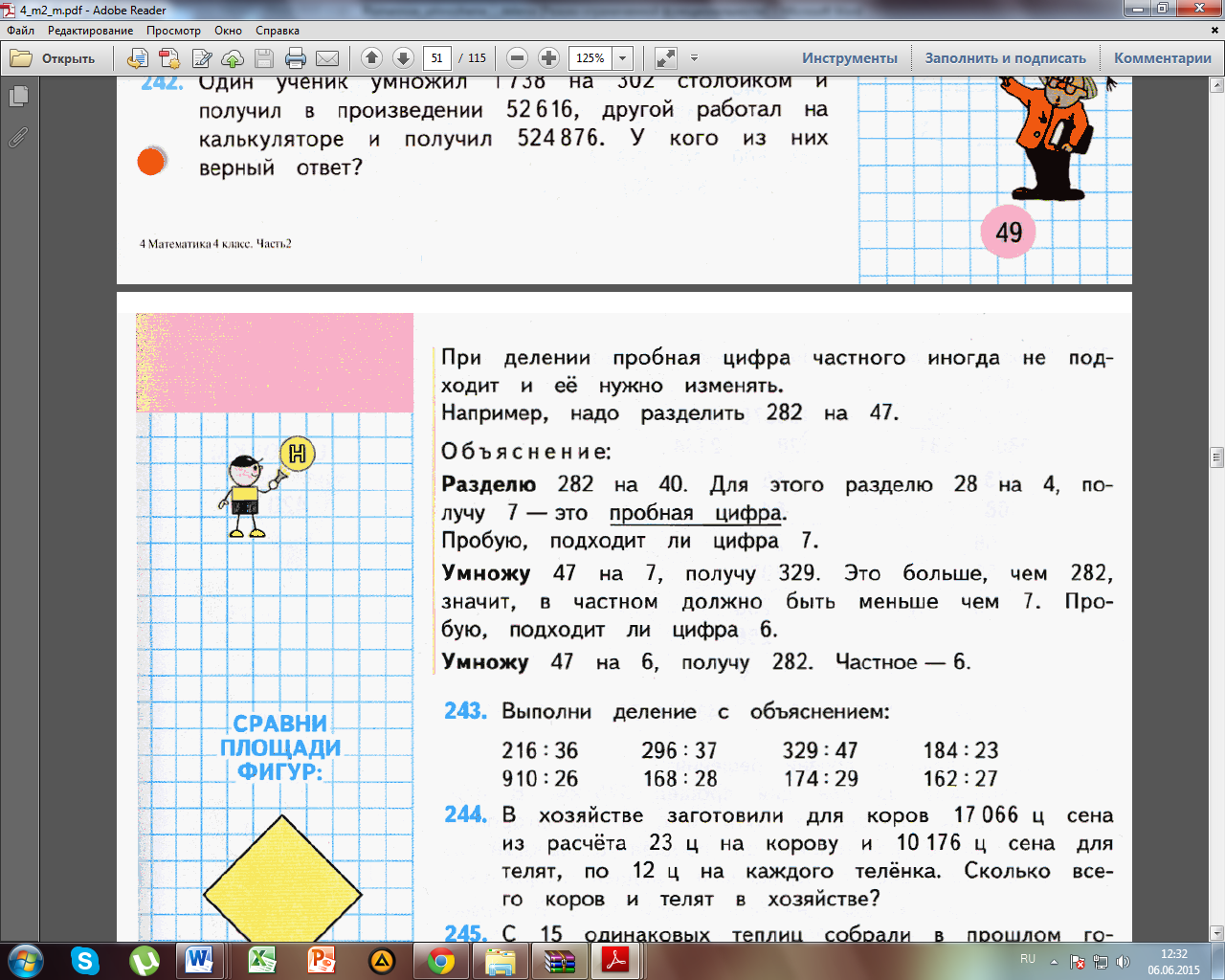
3. Вводим понятие « пробная цифра частного», т.е. рассматриваем случаи, когда при округлении делителя получаем такую цифру, которая не подходит, следовательно, её нужно либо увеличить, либо уменьшить. Её называют пробной цифрой.

М4М, ч.2, стр. 61

4. Деление на трёхзначное число, когда в частном одна цифра и число проб равно 1.

М4М, ч.2, стр. 72

738:246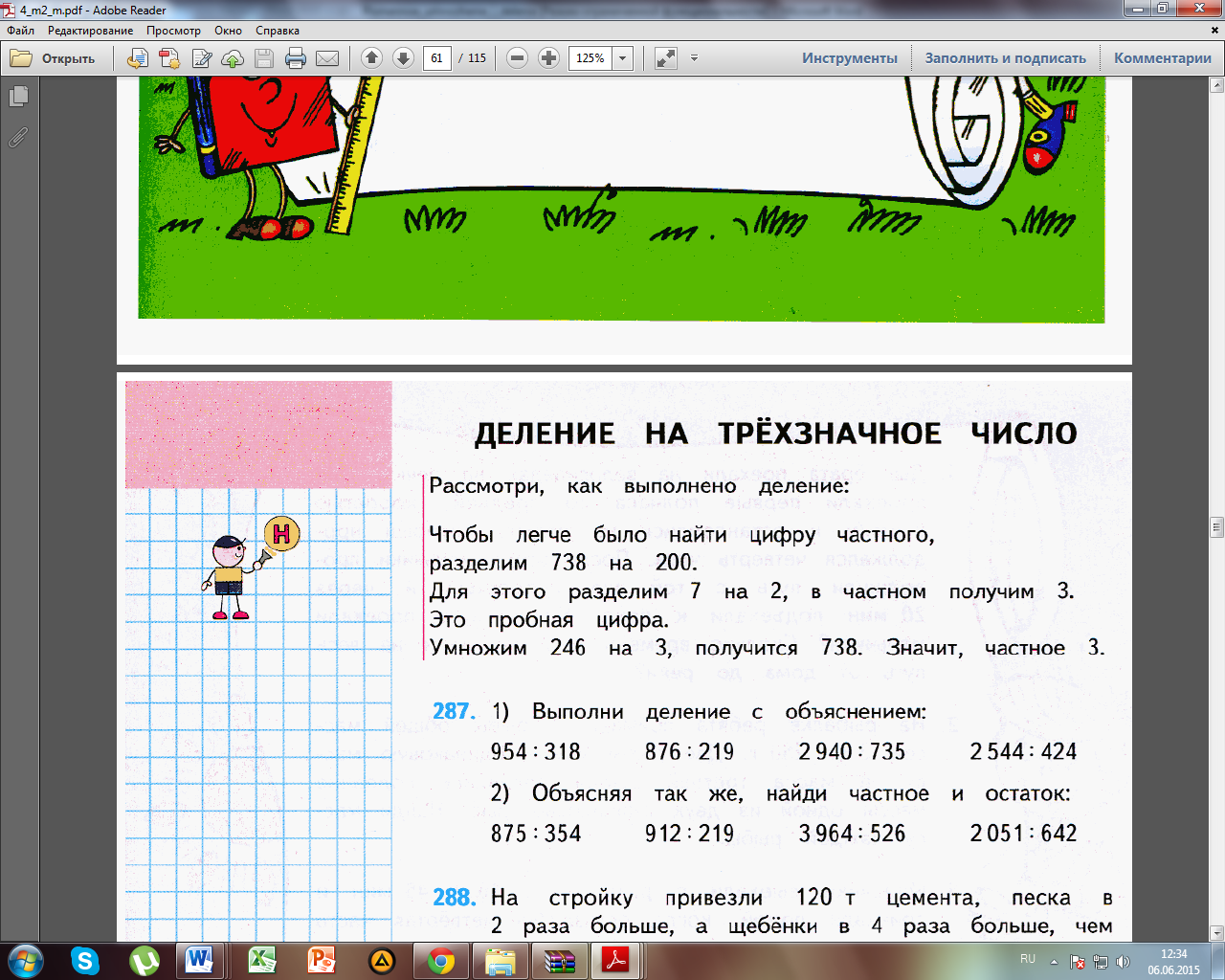

5. Деление на трёхзначное число в частном две цифры и число проб равно 1.

М4М, ч.2, стр. 73

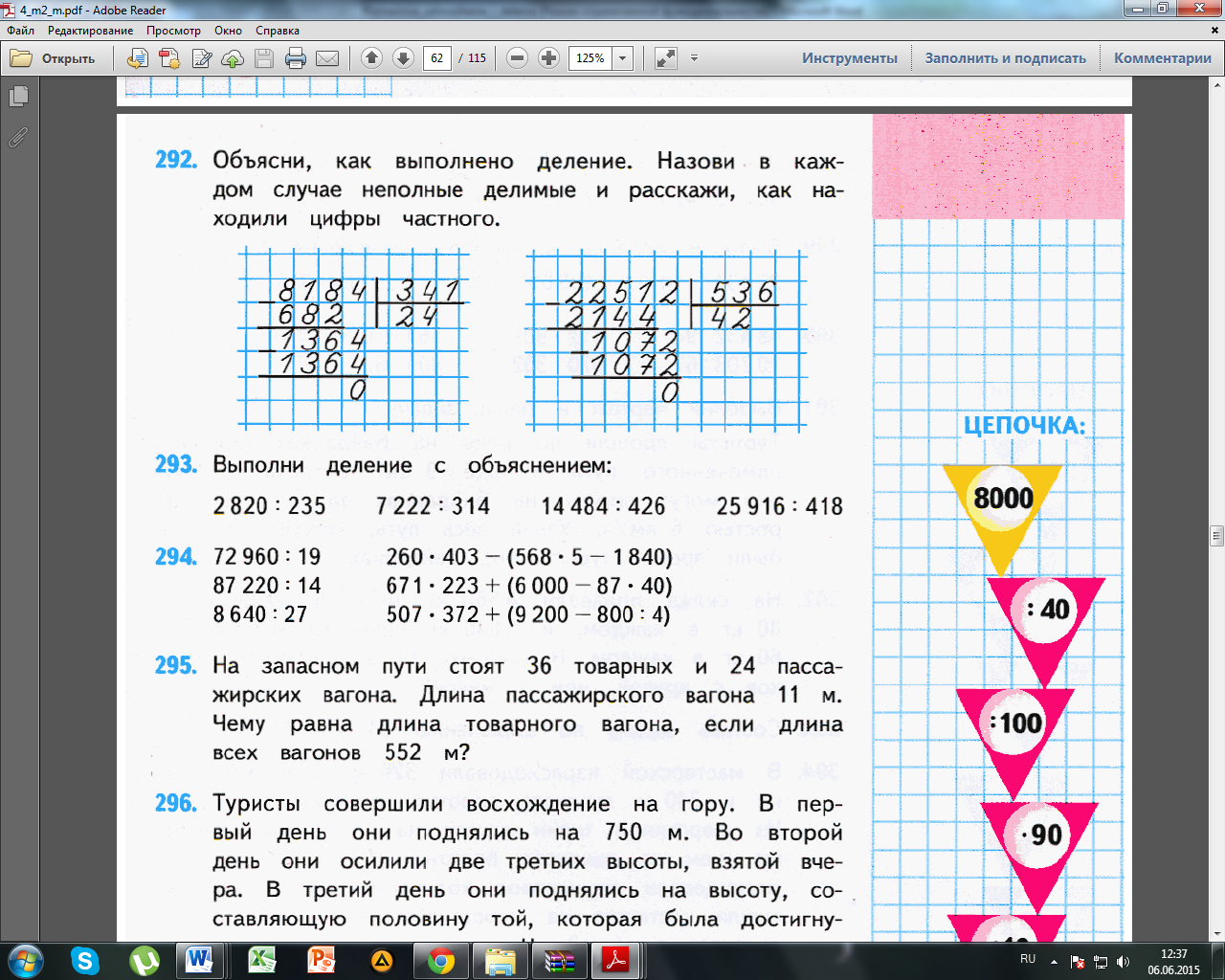
6. Деление на трёхзначное число, когда число проб больше 1

Далее до конца 4 класса отрабатывают вычислительные умения и навыки по данной теме.

Рассмотрите методику изучения этой темы по другим программам.

Программа Н.Б. Истоминой

Я рассмотрела учебники Н.Б. Истоминой и могу сделать вывод о том, что в данной программе частные случаи письменного деления на двух- и трехзначные числа не вводятся.

Программа И.И. Аргинской

По программе И.И. Аргинской данный прием начинают изучать в 4 классе. Рассмотрим поподробнее.

М4А, ч.1, стр. 132

На данной странице представлен прием письменного деления на двузначное число. Представлен небольшой алгоритм действий. После алгоритма можно увидеть интересные упражнения на закрепление данной темы.

М4А, ч.1, стр. 134

На данной странице изучают прием письменного деления на трехзначное число. Дан алгоритм действий, с помощью которого дети позже решают упражнения на усвоение нового материала.

М4А, ч.1, стр. 102

М4А, ч.1, стр. 112

М4А, ч.1, стр. 118

М4А, ч.1, стр. 130

Программа Г.В. Дорофеева

В учебниках Дорофеева при изучении приема письменного деления на двух- и трехзначные числа, детям встречаются частные случаи. Рассмотрим их поподробнее.

По программе Дорофеева данный прием и частные случаи начинают изучать в 4 классе.

М4Д, ч.1, стр. 83

На данной странице можно встретить сразу два частных случая:

1. Частный случай, когда в частном получается однозначное число и число проб равно 1.

232:58

2. Частный случай, когда в частном получаем двузначное число и число проб равно 1.

232:4

На этой странице вводится алгоритм действий, с помощью которого дети решают упражнения.

М4Д, ч.2, стр. 97

                       Вывод:

После того, как я рассмотрел все 4 программы, я хочу  сделать вывод о том, что почти во всех программах встречаются частные случаи. Исключением стала программа Н.Б. Истоминой. В ее программе я, к сожалению, не нашла частные случаи. Также важно отметить, что во всех учебниках эти случаи изучаются в 4 классе. Больше всего частных случаев можно встретить в учебнике М.И. Моро, поэтому можно сказать, что программа Моро является наиболее удобной и понятной для восприятия детьми. Также в программе Дорофеева приводится не так много частных случаев, но зато с подробным объяснением или с алгоритмом.

Познавательные статьи:



Алгоритмические операторы Matlab

Конструирование и порядок расчёта дорожной одежды

Исследования учёных: почему помогают молитвы?

Почему терпят неудачу многие предприниматели?