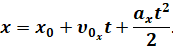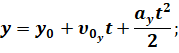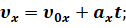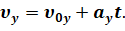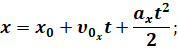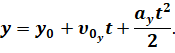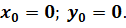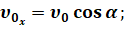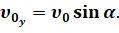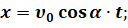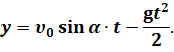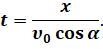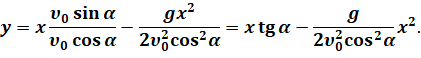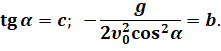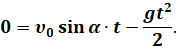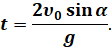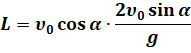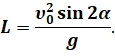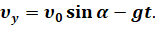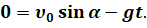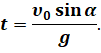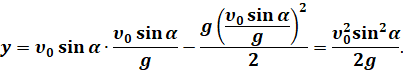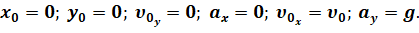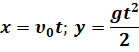Все тела при падении движутся одинаково: начав падать одновременно, они движутся с одинаковой скоростью.

Все тела при падении движутся одинаково: начав падать одновременно, они движутся с одинаковой скоростью.

Движение происходит с постоянным ускорением.

Для доказательства правоты Галилея Исаак Ньютон провёл очень простой и убедительный опыт. Он взял стеклянную трубку, в которую поместил дробинку, кусочек пробки, пушинку и так далее. Затем он перевернул трубку и наблюдал, как сначала упала дробинка, затем пробка и только потом — пушинка. Но вот когда он откачал из трубки почти весь воздух и повторил эксперимент, то увидел, как все три предмета упали на дно трубки одновременно.

Одновременное падение тел в разреженном воздухе доказывает, что все тела падают с одинаковым ускорением. Падение тел под действием только гравитационного поля Земли называется свободным падением. Поскольку сила тяжести, действующая на тело вблизи поверхности Земли в данной её точке, постоянна, то свободно падающее тело движется с постоянным ускорением, называемым ускорением свободного падения. Причём для всех тел в одном и том же месте оно одинаково и направлено по вертикали вниз.

Обратим внимание на то, что свободное падение — это не обязательно только движение вниз. Так, если мы подбросим камень, то он при своём свободном падении некоторое время будет двигаться вверх, уменьшая свою скорость до нуля, и лишь потом начнёт падать.

При изучении свободного падения тел мы будем рассматривать только такие движения, в которых сопротивлением воздуха можно пренебречь. Тогда эти движения будут описываться уже известными нам кинематическими уравнениями:

Теперь давайте изучим движение тела, начальная скорость которого направлена под некоторым углом к горизонту (или под углом к ускорению свободного падения). С таким видом движения приходится встречаться довольно часто. Например, так движется теннисный мячик после удара по нему ракеткой. Полет пуль и снарядов также представляет собой пример движения тел, брошенных под углом к горизонту.

Итак, найдём траекторию тела, брошенного под углом к горизонту с некоторой начальной скоростью.

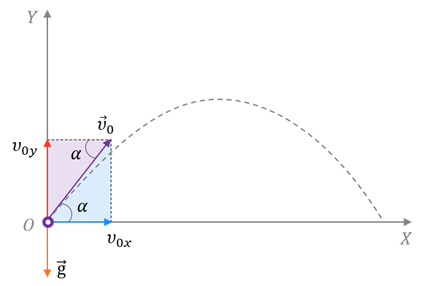
Для описания движения выберем две взаимно перпендикулярные оси координат таким образом, чтобы векторы начальной скорости и ускорения свободного падения лежали в одной плоскости. Начала отсчёта совместим с начальным положением тела.

Теперь запишем кинематические уравнения равноускоренного движения (а движение у нас действительно равноускоренное, потому что модуль и направление ускорения с течением времени не изменяются):

Так как начало координат совмещено с точкой бросания, то начальные координаты тела равны нулю:

В выбранной системе координат проекция вектора ускорения на ось Х равна нулю, а на ось Y — –g.

Из полученного рисунка видно, что проекцию вектора начальной скорости можно выразить через её модуль и косинус или синус угла, который этот вектор образует с положительным направлением оси:

Перепишем кинематические уравнения движения с учётом начальных условий:

Из этих формул следует, чтов горизонтальном направлении тело, брошенное под углом к горизонту, движется равномерно, а в вертикальном — равноускоренно.

В этом легко убедиться. Так, если посмотреть на такое движение тела сверху, то мы увидим, как оно движется вдоль прямой с постоянной скоростью. А если посмотреть на это движение сбоку, то мы сначала увидим, как шарик замедленно поднимается вверх, а потом ускоренно падает вниз.

Для построения траектории движения найдём её уравнение (то есть найдём зависимость у = у(х). Чтобы получить это уравнение нам с вами необходимо исключить время из уравнений движения. Для этого выразим из уравнения движения тела вдоль оси Х время:

И подставим его во второе уравнение:

Обратите внимание на то, что

После замены мы приходим к простой квадратичной функции, известной нам ещё из курса алгебры. Напомним, что её графиком является парабола. Причём ветви параболы будут направлены вниз, так как значение коэффициента b меньше нуля.

Таким образом мы с вами показали, что тело, брошенное под углом к горизонту, действительно движется по параболе (конечно при условии, что ускорение свободного падения постоянно).

Теперь давайте определим время полёта. Для этого воспользуемся уравнением движения тела вдоль оси OY. При этом учтём, что в момент падения тела на землю его координата становится равной нулю:

Решая простое квадратное уравнение, найдём формулу, по которой можно рассчитать время полёта тела:

Второй корень уравнения, равный нулю, соответствует моменту броска.

Теперь легко определить дальность полёта. Для этого подставляем найденное значение времени в уравнение движения тела вдоль оси Икс:

Полученное выражение можно упростить, если вспомнить о том, что удвоенное произведение синуса на косинус — это синус двойного угла:

Также мы можем найти максимальную высоту подъёма и время подъёма тела на эту высоту. Для этого воспользуемся уравнением скорости для равноускоренного движения в проекциях на ось Y:

Теперь учтём, что в верхней точке траектории проекция скорости на ось игрек равна нулю:

Решая простое линейное уравнение, найдём время подъёма тела на максимальную высоту:

Нетрудно заметить, что это время в два раза меньше времени всего полёта. Таким образом, получается, что сколько времени тело поднимается на максимальную высоту, столько же времени оно и опускается с неё.

Подставив полученное выражение для времени в уравнение движения вдоль оси игрек, найдём максимальную высоту подъёма тела:

Теперь давайте рассмотрим движение тела, брошенного горизонтально с некоторой высоты, и выясним, какой будет траектория этого тела. Для этого опять воспользуемся уравнениями движения, записанными в координатной форме:

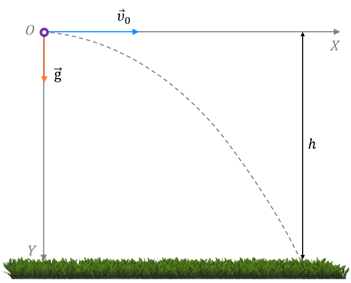
Для описания движения тела выберем две взаимно перпендикулярные о́си координат таким образом, чтобы векторы начальной скорости и ускорения свободного падения лежали в одной плоскости. При этом пусть положительное направление оси Y совпадает с направлением вектора ускорения свободного падения. Начало отсчёта совместим с начальным положением тела.

При таком выборе системы координат, начальные координаты тела равны нулю. Также равны нулю проекция начальной скорости на ось Y и проекция ускорения на ось X. Тогда:

Перепишем уравнения движения с учётом начальных условий:

Их анализ показывает, что в горизонтальном направлении тело движется равномерно, а в вертикальном — равноускоренно с ускорением свободного падения.

Когда скорость тела направлена горизонтально, оно движется по ветви параболы, вершина которой находится в точке бросания.

Предлагаем вам самостоятельно определить время и максимальную дальность полёта тела.

Таким образом, на основании рассмотренных нами примеров можно сделать вывод о том, что любое сложное движение можно представить, как сумму движений по двум независимым координатам. В этом состоит суть закона независимости движений.