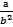Практическая работа. Использование логических высказываний и операций в алгоритмических конструкция

Цели: развитие знаний по составлению алгоритмов с использование логических высказываний и операций в алгоритмических конструкций.

Усвоить понятия: алгоритм как фундаментальное понятие информатики, способы описания, основные типы алгоритмов, освоить принципы решения задач с использованием основных алгоритмических конструкций.

Теоретические сведения

Как записываются логические выражения?

В записи логических выражений помимо арифметических операций сложения, вычитания, умножения, деления и возведения в степень используются операции отношения < (меньше), <= (меньше или равно), > (больше), >= (больше или равно), = (равно), <> (не равно), а также логические операции и, или, не.

Примеры записи логических выражений, истинных при выполнении указанных условий.

Условие

Запись на школьном алгоритмическом языке

  Дробная часть вещественого числа a равна нулю

int(a) = 0

  Целое число a — четное

mod(a, 2) = 0

  Целое число a — нечетное

mod(a, 2) = 1

  Целое число k кратно семи

mod(a, 7) = 0

  Каждое из чисел a, b положительно

(a>0) и (b>0)

  Только одно из чисел a, b положительно

((a>0) и (b<=0)) или
((a<=0) и (b>0))

  Хотя бы одно из чисел a, b, c является отрицательным

(a<0) или (b<0) или (c<0)

  Число x удовлетворяет условию a < x < b 

(x>a) и (x<b)

  Число x имеет значение в промежутке

(x>=1) и (x<=3)

  Целые числа a и b имеют одинаковую четность

((mod(a, 2)=0) и (mod(b, 2)=0) или ((mod(a, 2)=1) и (mod(b, 2)=1))

  Точка с координатами (x, y) лежит в круге радиуса r  с центром в точке (a, b)

(x-a)**2 + (y-b)**2 < r*r

  Уравнение ax^2 + bx + c = 0 не имеет действительных корней

b*b - 4*a*c < 0

  Точка (x, y) принадлежит первой или третьей   четверти

((x>0) и (y>0)) или
((x<0) и (y>0))

  Точка (x, y) принадлежит внешности единичного круга   с центром в начале координат или его второй четверти

(x*x + y*y > 1) или
((x*x + y*y <= 1) и (x<0) и (y>0))

  Целые числа a и b являются взаимнопротивоположными

a = -b

  Целые числа a и b являются взаимнообратными

a*b = 1

  Число больше среднего арифметического чисел b, c, d

a > (b+c+d) / 3

  Число a не меньше среднего геометрического чисел b, c, d

a >= (b+c+d) ** (1/3)

  Хотя бы одна из логических переменных F1 и F2 имеет   значение да

F1 или F2

  Обе логические переменые F1 и F2 имеют значение да

F1 и F2

  Обе логические переменые F1 и F2 имеют значение нет

не F1 и не F2

  Логическая переменная F1 имеет значение да, а   логическая переменная F2 имеет значение нет

F1 и не F2

  Только одна из логических переменных F1 и F2   имеет значение да

(F1 и не F2) или (F2 и не F1)

Решение любой задачи на ЭВМ можно разбить на следующие этапы: разработка алгоритма решения задачи, составление программы решения задачи на алгоритмическом языке, ввод программы в ЭВМ, отладка программы (исправление ошибок), выполнение программы на ПК, анализ полученных результатов.

Первый этап решения задачи состоит в разработке алгоритма.

Алгоритм – это точная конечная система правил, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения после конечного числа шагов искомого результата.

Алгоритм может быть описан одним из трех способов:

- словесным (пример в начале раздела);

- графическим (виде специальной блок-схемы);

- с помощью специальных языков программирования.

Блок-схема – распространенный тип схем, описывающий алгоритмы или процессы, изображая шаги в виде блоков различной формы, соединенных между собой стрелками.

1. Линейный алгоритм – это такой алгоритм, в котором все операции выполняются последовательно одна за другой.

2. Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие.

3. Алгоритмы циклической структуры.

Циклом называют повторение одних и тех же действий (шагов). Последовательность действий, которые повторяются в цикле, называют телом цикла. 

Циклические алгоритмы подразделяют на алгоритмы с предусловием, постусловием и алгоритмы с конечным числом повторов. В алгоритмах с предусловием сначала выполняется проверка условия окончания цикла и затем, в зависимости от результата проверки, выполняется (или не выполняется) так называемое тело цикла.

Задания.

Задание 1. Запишите в обычной математической форме арифметические выражения:

а) a / b ** 2; Например:  

б) a+b/c+1;

в) 1/a*b/c;

г) a**b**c/2;

д) (a**b)**c/2;

е) a/b/c/d*p*q;

ж) x**y**z/a/b;

з) 4/3*3.14*r**3;

и) b/sqrt(a*a+b);

к) d*c/2/R+a**3;

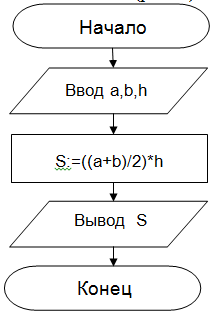
Задание 2. Определить площадь трапеции по введенным значениям оснований (a и b) и высоты (h).

Записать решение задачи на алгоритмическом языке

Рисунок 1. Блок-схема линейного алгоритма

Задание 3. Определить среднее арифметическое двух чисел, если a положительное и частное (a/b) в противном случае.

Запись решения задачи на алгоритмическом языке:

Алг числа

  вещ a,b,c

Нач

  ввод a,b

  если a>0

        то     с:=(a+b)/2

       иначе с:=a/b

    все

    вывод с

кон

Записать алгоритм в виде блок-схемы

Контрольные вопросы

Что такое алгоритм?

Свойства алгоритма.

Способы записи алгоритма.

Основные элементы блок-схемы.

Виды алгоритмов.

Отличительные особенности алгоритмов с предусловием и постусловием.

Выполненные в тетради задания выслать на адрес электронной почты: zhulanova.yulia@yandex.ru

Познавательные статьи:



Техника прыжка в длину с разбега

Организация работы процедурного кабинета

Области применения синхронных машин

Оптимизация по Винеру и Калману