
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первый проректор по учебной работе
Утверждаю Первый проректор по учебной работе ________________А.Н. Прокофьев «____»____________20____ г.
ИНФОКОММУНИКАЦИОННЫЕ СИСТЕМЫ И СЕТИ
Использование математической логики при проектировании вычислительных сетей Методические указания к выполнению лабораторной работы для студентов дневной формы обучения по направлению 051000 Профессиональное обучение
Брянск 20014
УДК 629.42.02/.06(07)+621.313.2(07)
Инфокоммуникационные системы и сети: Методические указания к выполнению лабораторной работы для студентов дневной формы обучения по направлению 051000 “Профессиональное обучение”, Отрасль: информатика, вычислительная техника и компьютерные технологии - Брянск: БГТУ, 2014.- 11 с.
Разработал: ст. преп. И.Е.Грабежов
Рекомендовано кафедрой «Компьютерные технологии и системы» БГТУ (протокол № от )
Научный редактор В.А.Аверченков Редактор издательства Л.Н.Мажугина Компьютерный набор И.Е.Грабежов Иллюстрации И.Е.Грабежов
Темплан 2014 г., п.96 __________________________________________________________ Подписано в печать 16.03.07. Формат 60х84 1/16 Бумага офсетная. Офсетная печать. Усл.печ.л. 0,46. Уч.-изд.л. 0,46 Тираж 40 экз. Заказ Бесплатно.
Брянский государственный технический университет. 241035, Брянск, бульвар 50-летия Октября, 7, БГТУ. 54-90-49. Лаборатория оперативной полиграфии БГТУ, ул. Институтская, 16. Цель: 1. Закрепить знания, полученные на лекциях. 2. Изучить методы решения задач математической логики. 3. Получить практические навыки в использовании математической логики в построении локальных вычислительных сетей.
Теоретические сведенья Алгебра логики – раздел математической логики, в котором изучаются логические операции над высказываниями. Алгебру логику называют также алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения. В булевой алгебре высказывания принято обозначать прописными латинскими буквами: A, B, X, Y. В алгебре Буля введены три основные логические операции с высказываниями. Сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений. Логические выражения могут быть простыми и сложными. Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В простом логическом выражении возможно только два результата (значения) – либо «истина», либо «ложь». Значения логических выражений определяют множество чисел, на которыми выполняются операции. Это множество двоичных чисел, т.е. в него входят только два числа: 1 – “истина”, 0 – “ложь”. Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания. В качестве основных логических операций в сложных логических выражениях используются следующие: • НЕ (логическое отрицание, инверсия); • ИЛИ (логическое сложение, дизъюнкция); • И (логическое умножение, конъюнкция).
Логическое отрицание является одноместной (унарной) операцией, так как в ней участвует одно высказывание. Логическое сложение и умножение – двуместные операции, в них участвует два высказывания. Существуют и другие операции, например операции следования и эквивалентности, правило работы которых можно вывести на основании основных операций. Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении, например: – таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции; – в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции; – если число высказываний в логическом выражении N, то таблица истинности будет содержать 2N строк, так как существует 2N различных комбинаций возможных значений аргументов. Операция НЕ – логическое отрицание (инверсия). Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее: • если исходное выражение истинно, то результат его отрицания будет ложным; • если исходное выражение ложно, то результат его отрицания будет истинным. Для операции отрицания НЕ приняты следующие условные обозначения: не А, Ā, not A, А. Результат операции отрицания НЕ определяется следующей таблицей истинности: A не А Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.
Примеры отрицания. Принцип работы переключателя настольной лампы таков: если лампа горела, переключатель выключает ее, если лампа не горела – включает ее. Такой переключатель можно считать электрическим аналогом операции отрицания.
Операция ИЛИ — логическое сложение (дизъюнкция, объединение). Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений. Применяемые обозначения: А или В, А V В, A or B, A + B. Результат операции ИЛИ определяется следующей таблицей истинности: A B А или B Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В – ложны. Примеры логического сложения. Кто хоть однажды использовал елочную гирлянду с параллельным соединением лампочек, знает, что гирлянда будет светить до тех пор, пока цела хотя бы одна лампочка. Логическая операция ИЛИ чрезвычайно схожа с работой подобной гирлянды, ведь результат операции ложь только в одном случае — когда все аргументы ложны.
Операция И — логическое умножение (конъюнкция). Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения. Применяемые обозначения: А и В, А Λ В, A & B, A and B. Результат операции И определяется следующей таблицей истинности: A B А и B Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях. Примеры логического умножения. Логическую операцию И можно сравнить с последовательным соединением лампочек в гирлянде. При наличии хотя бы одной неработающей лампочки электрическая цепь оказывается разомкнутой, то есть гирлянда не работает. Ток протекает только при одном условии — все составляющие цепи должны быть исправны. Операция «ЕСЛИ-ТО» – логическое следование (импликация). Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия. Применяемые обозначения: если А, то В; А влечет В; if A then В; А→ В. Таблица истинности: A B А → B Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно. Примеры операции следования. 2. Рассмотрим два высказывания: А {х делится на 9}, В {х делится на 3}. Операция А → В означает следующее: «Если число делится на 9, то оно делится и на 3». Рассмотрим возможные варианты: ■ А – ложно, В – ложно (1-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А – ложно, то и В – ложно». Например, х = 4, 17, 22. ■ А – ложно, В – истинно (2-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А – ложно, то В – истинно». Например, х = б, 12, 21. ■ А – истинно, В – ложно (3-я строка таблицы истинности). Невозможно найти такие числа, которые делились бы на 9, но не делились на 3. Истинная предпосылка не может приводить к ложному результату импликации. ■ А – истинно, В – истинно (4-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А – истинно, то и В – истинно». Например, х = 9, 18, 27.
Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность). Применяемое обозначение: А ↔ В, А ~ В. Таблица истинности: A B А↔B Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны. Примеры операции эквивалентности: 1. День сменяет ночь тогда и только тогда, когда солнце скрывается за горизонтом; 2. Добиться результата в спорте можно тогда и только тогда, когда приложено максимум усилий. Приоритет логических операций 1. Действия в скобках. 2. Инверсия. 3. Конъюнкция ( & ). 4. Дизъюнкция ( V ). 5. Импликация ( → ). 6. Эквивалентность ( ↔ ).
Содержание отчета 1. Титульный лист. 2. Цель работы. 3. Таблицы истинности. 4. Вывод. При выполнении работы необходимо представить полные таблицы для каждого выражения. Вывод должен содержать номер выражения, фрагмент таблицы истинности которого представлен в задании.
Задания Варианты:
1) X Ú Y Ú Z 2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z
2) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 1) X Ú Y Ú Z 2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z
1) X Ù Y Ù Z 2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ù Y Ù Z
1) X Ù Y Ù Z2) X Ú Y Ú Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z
1) A→(A Ú B) 2) A Ù B 3) A→B 4) A Ù B
1) X Ù Y Ù Z2) X Ú Y Ú Z 3) X Ù (Y Ú Z) 4) (X Ú Y) Ù Z
7) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 1) X Ú Y Ù Z 2) X Ú Y Ú Z 3) X Ù Y Ú Z 4) X Ú Y Ù Z
8) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 1) (X Ù Y) Ù Z2) (X Ú Y) Ú Z3) (X Ù Y) Ú Z 4) (X Ú Y) Ù Z
10) Символом F обозначена логическая функция от двух аргументов (A и B), заданная таблицей истинности. Какое выражение соответствует F? 1) A→((A Ù B)) 2) A Ù B 3) A→B 4) A Ù B
1) X Ù Y Ù Z 2) X Ú Y Ú Z 3) X Ú Y Ú Z 4) X Ù Y Ù Z
1) X Ú Y Ú Z 2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z
1) X Ú Y Ú Z2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z
1) X Ù Y Ù Z2) X Ù Y Ù Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z
1) X Ù Y Ù Z 2) X Ú Y Ú Z 3) X Ú Y Ú Z 4) X Ù Y Ù Z
1) X Ù Y Ú Z 2) X Ú Y Ú Z 3) (X Ú Y) Ù Z 4) (X Ú Y) →Z
1) (X Ú Y)→Z 2) (X Ú Y)→Z 3) X Ú (Y→Z) 4) X Ú Y Ù Z
1) X Ù Y Ú Z 2) (X Ú Y)→Z 3) (X Ú Y)Ù Z 4) X→Y Ú Z
1) (X→Y)→Z2) X→(Y→Z) 3) X Ú Y→Z 4) X Ú Y Ù Z
1) (X Ú Y) Ù Z 2) X Ù Y Ú Z 3) (X→Y) Ù Z 4) X Ù(Y Ú Z)
1) (X→Z)Ù Y2) X Ù Y Ú Z 3) X Ú Y Ú Z 4) X Ù(Y →Z)
1) X Ù Y Ú Z 2) (X Ú Y)→Z 3) (X Ú Y)Ù Z 4) X→(Y Ú Z)
1) (X Ú Y)→Z 2) (X Ú Y)→Z 3) X Ú(Y→Z) 4) X Ú Y Ù Z
24) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 1) X Ù Y Ù Z2) X Ù Y Ù Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z
1) X Ù Y Ù Z2) X Ù Y Ù Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z
X Y Z F 26) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 1) X Ù Y Ù Z2) X Ú Y Ú Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z
27) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 1) X Ù Y Ù Z2) X Ù Y Ù Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z
1) X Ú Y Ú Z2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z
1) (X ~ Z) Ù (X→Y) 2) (X ~ Z) Ù (X→Y) 3) (X ~ Z) Ù (X→Y) 4) (X ~ Z) Ù (Y→Z) Знак ~ означает «эквивалентность», то есть «X ~ Z» значит «значения XиZ совпадают».
X Y Z F 30) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 1) X Ú Y Ú Z2) X Ù Y Ù Z 3) X Ù (Y Ú Z)
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 48; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 1) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
1) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
 3) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
3) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 4) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
4) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?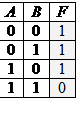 5) Символом F обозначена логическая функция от двух аргументов (A и B), заданная таблицей истинности. Какое выражение соответствует F?
5) Символом F обозначена логическая функция от двух аргументов (A и B), заданная таблицей истинности. Какое выражение соответствует F? 6) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
6) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
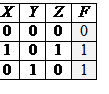 9) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
9) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?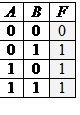 1) X Ù Y Ù Z2) X Ú Y Ú Z 3) X Ù Y Ú Z 4) X Ú Y Ù Z
1) X Ù Y Ù Z2) X Ú Y Ú Z 3) X Ù Y Ú Z 4) X Ú Y Ù Z 11) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
11) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 12) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
12) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?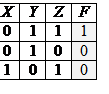 13) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
13) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 14) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
14) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 15) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
15) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?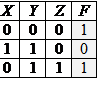 16) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
16) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 17) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
17) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 18)Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
18)Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 19)Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
19)Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 20) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
20) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 21) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
21) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 22) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
22) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? 23) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
23) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
 25) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
25) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
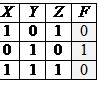 29) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
29) Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?


