Комбинаторика — раздел математики о вычислении количества различных комбинаций каких-либо элементов.

 

1. Понятие комбинаторики

Теория:

Комбинаторика — раздел математики о вычислении количества различных комбинаций каких-либо элементов.

В заданиях по комбинаторике обычно нужно выяснить, возможно ли составить комбинацию определённого вида, и сколько различных комбинаций можно составить.

 

Пример:

1. сколько различных трёхзначных номеров телефона можно составить из пяти цифр? (Ответ: 125.)

2. Сколькими различными способами можно составить танцевальную пару, если в коллективе 3 мальчика и 4 девочки? (Ответ: 12.)

3. Сколькими различными способами можно образовать пару дежурных, если в классе остались Надя, Вика, Саша и Юра? (Ответ: 6.)

4. Сколькими различными способами можно выбрать двух учеников (одного — чистить доску, второго — подметать пол), если в классе остались Надя, Вика, Саша и Юра? (Ответ: 12.)

Один из способов решения задач комбинаторики — это рассмотреть все возможные комбинации элементов, что называется полным перебором вариантов.

 

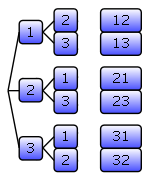
Древовидная диаграмма

Древовидная диаграмма — один из способов показать и систематизировать все размещения. С помощью древовидной диаграммы осуществляется полный перебор.

Сколько различных двузначных чисел можно составить из цифр 1, 2 и 3, если каждую использовать только один раз?

Решение:

составляется древовидная диаграмма.

Ответ: можно составить 6 различных чисел.

 

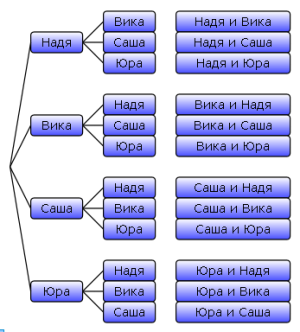
Пример:

рассмотрим 3-й пример (см. выше):

сколькими различными способами можно образовать пару дежурных, если в классе остались Надя, Вика, Саша и Юра?

На древовидной диаграмме видно, что можно образовать только 6 пар дежурных (Надя и Вика, Надя и Саша, Надя и Юра, Вика и Саша, Саша и Юра, Вика и Юра), т. к. каждая пара повторяется 2 раза.

Рассмотрим 4-й пример:

сколькими различными способами можно выбрать двух учеников (одного — чистить доску, второго — подметать пол), если в классе остались Надя, Вика, Саша и Юра?

Используется та же древовидная диаграмма, но в данном случае ответ будет — 12 пар, т. к. каждая пара из диаграммы отличается. Если детей поменять местами, они выполняют уже другие функции.

С помощью древовидной диаграммы были получены различные результаты, т. к. в 3 и 4 примере были рассмотрены различные виды комбинаций: сочетания и размещения.

 

Такого рода диаграммы в подробностях удобно рисовать только для сравнительно небольшого числа вариантов, а, например, для сотен комбинаций дерево вариантов целиком не нарисуешь. Тогда приходится действовать по-другому. Чаще всего при различных подсчётах используют правило умножения:

для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.