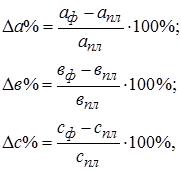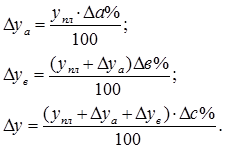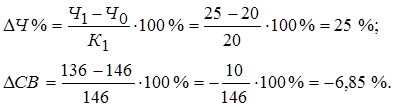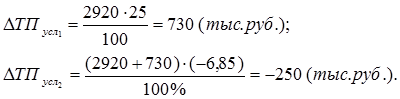Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исходные данные для факторного анализаСодержание книги
Поиск на нашем сайте
Задача 1.1 (для решения) Определить среднюю задолженность предприятия по кредитам. Проанализировать её изменения в отчётном году и по сравнению с прошлым годом. Исходные данные:
Дата Фактическая задолженность, тыс. руб. Дата Фактическая задолженность, тыс. руб. 01.01.* 11.2 01.08. 11.7 01.02. 12.6 01.09. 7.4 01.03. 9.6 01.10.* 12.4 01.04.* 15.7 01.11. 18.7 01.05. 5.8 01.12. 13.2 01.06. 8.7 01.01 13.2 01.07.* 6.1
*Квартальные даты Средняя задолженность по кредитам в прошлом году составила: a) По месячным датам – 9,7 т. р. b) По квартальным датам – 8.2 т.р.
Решение:
1.3. Методика факторного анализа Под экономическим факторным анализом понимается постепенный переход от исходной факторной системы к конечной факторной системе, раскрытие полного набора прямых, количественно измеримых факторов, оказывающих влияние на изменение результативного показателя. По характеру взаимосвязи между показателями различают методы детерминированного и стохастического факторного анализа. Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер. Основные свойства детерминированного подхода к анализу: · построение детерминированной модели путем логического анализа; · наличие полной (жесткой) связи между показателями; · невозможность разделения результатов влияния одновременно действующих факторов, которые не поддаются объединению в одной модели; · изучение взаимосвязей в краткосрочном периоде. Различают четыре типа детерминированных моделей: Аддитивные модели представляют собой алгебраическую сумму показателей и имеют вид
К таким моделям, например, относятся показатели себестоимости во взаимосвязи с элементами затрат на производство и со статьями затрат; показатель объема производства продукции в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в отдельных подразделениях. Мультипликативные модели в обобщенном виде могут быть представлены формулой
Примером мультипликативной модели является двухфакторная модель объема реализации
где Ч - среднесписочная численность работников; CB - средняя выработка на одного работника.
Кратные модели:
Примером кратной модели служит показатель срока оборачиваемости товаров (в днях) . ТОБ.Т:
где ЗТ - средний запас товаров; ОР - однодневный объем реализации.
Смешанные модели представляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений:
Примерами таких моделей служат показатели затрат на 1 руб. товарной продукции, показатели рентабельности и др. Детализация факторного анализа во многом определяется числом факторов, влияние которых можно количественные оценить, поэтому большое значение в анализе имеют многофакторные мультипликативные модели. В основе их построения лежат следующие принципы: · место каждого фактора в модели должно соответствовать его роли в формировании результативного показателя; · модель должна строиться из двухфакторной полной модели путем последовательного расчленения факторов, как правило качественных, на составляющие; · при написании формулы многофакторной модели факторы должны располагаться слева направо в порядке их замены. Построение факторной модели – первый этап детерминированного анализа. Далее определяют способ оценки влияния факторов. Способ цепных подстановок заключается в определении ряда промежуточных значений обобщающего показателя путем последовательной замены базисных значений факторов на отчетные. Данный способ основан на элиминировании. Элиминировать – значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. При этом исходя из того, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения. потом изменяются два при неизменности остальных и т.д. В общем виде применение способа цепных постановок можно описать следующим образом: y0 = a0 . b0.c0; ya = a1 . b0.c0; yb = a1 . b1.c0; y1 = a1 . b1.c1, где a0, b0, c0 - базисные значения факторов, оказывающих влияние на обобщающий показатель у; a1 , b1, c1 - фактические значения факторов; ya, yb, - промежуточные изменения результирующего показателя, связанного с изменением факторов а, b, соответственно. Общее изменение Dу=у1–у0 складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:
Dу = SDу (а,b,с) = Dуа + Dуb +Dуc Dуа = уа – у0; Dуb = ув – уа; Dус = у1 – ув.
Рассмотрим задачу 2: Таблица 2 Показатели Условные обозначения Базисные значения (о) Фактические значения (1) Изменение Абсолютное (+,- ) Относительное (%) Объем товар-ной продукции, тыс. руб.
ТП
3400-2920=480 +480 3400:2920х100%= 116,40 Количество работников, чел
Ч
25-20=5 +5 25:20х100%= 125,00 Выработка на одного работа-ющего, тыс. руб
СВ 2920:20= 3400:25= 136-146= - 10 -10 136:146х100%= 93,15 Анализ влияния на объем товарной продукции количества работников и их выработки проведем описанным выше способом на основе данных табл.2. Зависимость объема товарной продукции от данных факторов можно описать с помощью мультипликативной модели: ТП= Ч . СВ, Сначала мы рассчитываем только по базисным значениям (0) ТПо = Чо . СВо = 20 . 146 = 2920 (тыс. руб.).
Тогда влияние изменения величины количества работников на обобщающий показатель можно рассчитать по формуле: Затем при каждом последующем расчете меняем базисный показатель (0) на фактическое значение (1) ТП усл1 = Ч1 . СВо = 25 . 146 = 3650 (тыс. руб.), DТПусл1 = ТПусл1 – ТПо = 3650 – 2920 = 730 (тыс. руб.). Далее определим влияние изменения выработки работников на обобщающий показатель ТП1 = Ч1 . СВ1 = 25 . 136 = 3400 (тыс. руб.), DТП усл2 = ТП1 – ТПусл1 = 3400 – 3650 = - 250 (тыс. руб.). Таким образом, на изменение объема товарной продукции положительное влияние оказало изменение на 5 чел. численности работников, что вызвало увеличение объема продукции на 730т. руб. и отрицательное влияние оказало снижение выработки на 10т.руб., что вызвало снижение объема на 250 тыс. руб. Суммарное влияние двух факторов привело к увеличению объема продукции на 480 тыс. руб. Преимущества данного способа: универсальность применения, простота расчетов. Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют определенные правила, определяющие последовательность подстановки: · при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов; · если модель представлена несколькими количественными и качественными показателями, последовательность подстановки определяется путем логического анализа. Под количественным факторами при анализе понимают те, которые выражают количественную определенность явлений и могут быть получены путем непосредственного учета (количество рабочих, станков, сырья и т.д.). Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, средняя продолжительность рабочего дня и т.д.). Способ абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки: y0 = a0 . b0. c0; Dуа = Dа . b0 . с0; Dуb = Db . а1 . с0; Dус = Dс . а1 . b1; у1 = а1 . b1 . с1; Dу = Dуа + Dуb + Dуc. Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных и смешанных моделях вида у = (а – в).с. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах. Для мультипликативных моделей типа у = а . в . с методика анализа следующая: · находят относительное отклонение каждого факторного показателя:
· определяют отклонение результативного показателя у за счет каждого фактора
Пример. Воспользовавшись данными табл. 2, проведем анализ способом относительных разниц. Относительные отклонения рассматриваемых факторов составят:
Рассчитаем влияние на объем товарной продукции каждого фактора:
Результаты расчетов те же , что и при использовании предыдущего способа. Интегральный метод позволяет избежать недостатков, присущих методу цепной подстановки, и не требует применения приемов по распределению неразложимого остатка по факторам, т.к. в нем действует логарифмический закон перераспределения факторных нагрузок. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям. Операция вычисления определенного интеграла решается с помощью ПЭВМ и сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы.
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 4; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.45 (0.008 с.) |

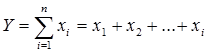 .
.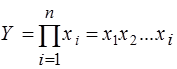 .
.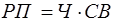 ,
,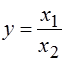 .
.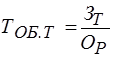 ,
,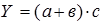 ; Y =
; Y = 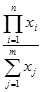 ; Y =
; Y = 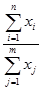 ; Y =
; Y = 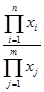 .
.