
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конспект урока "Сфера и шар"
На этом уроке мы рассмотрим понятия сферы и шара. Дадим их определения. Назовем некоторые из элементов сферы и шара. А также узнаем, как находят объем шара и площадь сферы. Итак, рассмотрим понятия сферы и шара. Нас окружают различные тела. Формы предметов окружающего мира очень разнообразны. Среди них встречаются так называемые «круглые тела». Особое место среди круглых тел занимает шар. Итак, шар– это геометрическое тело. Форму, близкую к форме шара, имеют арбуз, апельсин, планеты. Некоторые архитектурные сооружения. Декоративным растениям также придают форму шара.
Поверхность шара называют сферой. Можно сказать, что сфера – это как-бы оболочка или граница шара. Как окружность, есть граница круга, так и сфера – это граница шара. Представление о сфере дают полые круглые предметы, например, футбольный и теннисный мяч, мыльные пузыри или, ставший в наше время популярным видом отдыха, «аквазорбинг». Зорб дает представление о сфере.
Чтобы уяснить разницу между понятиями шар и сфера, давайте внимательно посмотрим на рисунок.
Перед вами изображены воздушный шар и бильярдный шар. Оба этих предмета называют шарами. Однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри. Определение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
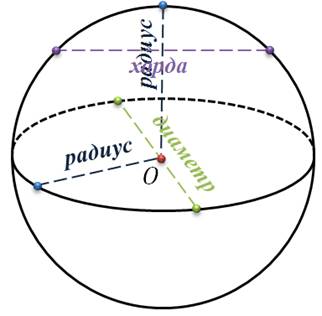
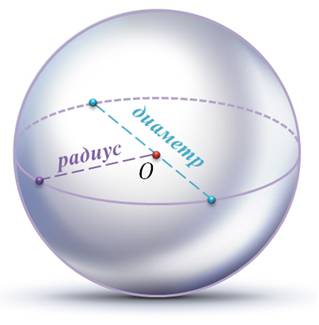
Данная точка называется центром сферы, а данное расстояние – радиусом сферы. Любой отрезок, соединяющий центр сферы с какой-либо ее точкой, также называется радиусом сферы. Отрезок, соединяющий две точки сферы, называется хордой сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. Понятно, что Тело, ограниченное сферой, называется шаром. Определение. Шар – это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Т.е. отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара. Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам.
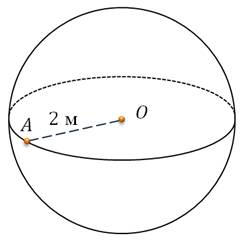
Рассмотрим чертеж.
Перед нами математическое изображение шара. Точка О – это центр шара. Все точки поверхности шара одинаково удалены от центра шара. Понятно, что шар радиуса r с центром О содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем r (включая саму точку О), и не содержит других точек. Хотелось бы обратить внимание на то, что шар может быть получен путем вращения полукруга вокруг его диаметра. При этом сфера образуется в результате вращения полуокружности. Пользуясь принципом Кавальери, можно доказать, что В отличие от боковых поверхностей цилиндра и конуса сферу нельзя развернуть так, чтобы получилась плоская фигура.
Поэтому для сферы не подходит способ вычисления площади с помощью развертки. Вопрос о том, что понимать под площадью сферы и как ее вычислять, мы будем подробно рассматривать в курсе стереометрии в одиннадцатом классе.
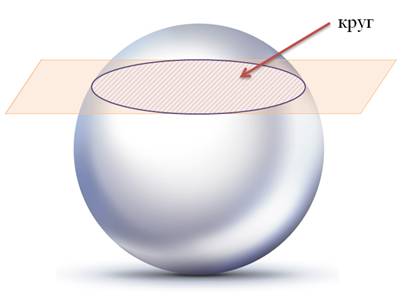
Сейчас только отметим, что для площади S сферы радиуса r получается формула: Если шар разрезать, то фигура, образованная на срезе, есть круг.
Сам же срез называют сечением. В свою очередь, сечение сферы плоскостью есть окружность. Задача.Найдите объем шара и площадь сферы с радиусом Решение:
Ответ: Немного из истории. Оба слова «шар» и «сфера» происходят от греческого слова «сфайра» – мяч, шар. В древности сфера и шар были в большом почете. Пифагорейцы учили о существовании десяти сфер Вселенной, по которым якобы двигаются небесные тела. Они утверждали, что расстояние этих тел друг от друга пропорциональны интервалам музыкальной гаммы. В этом усматривали элементы мировой гармонии. Отсюда пошло выражение «музыка сферы». Аристотель считал, что шарообразная форма, как наиболее совершенная, свойственна Солнцу, Земле, Луне и всем мировым телам. Так же он полагал, что Земля окружена рядом концентрических сфер. Подведем итоги урока. На этом уроке мы рассмотрели понятия сферы и шара. Узнали, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. А шар – это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Назвали некоторые из элементов сферы и шара. А также узнали, как находят объем шара и площадь сферы.
|
||||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.83 (0.005 с.) |




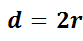 .
.
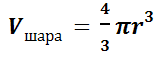 .
.
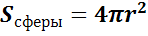 .
.
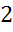 метра. Число
метра. Число 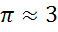 .
.
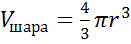
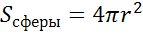
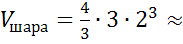
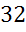 (м3)
(м3)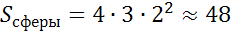 (м2)
(м2)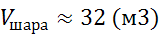 ,
, 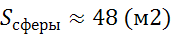 .
.


