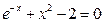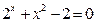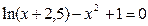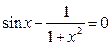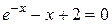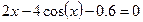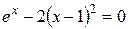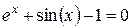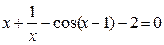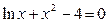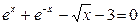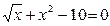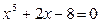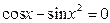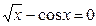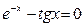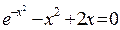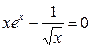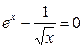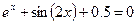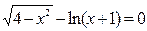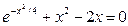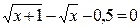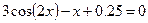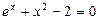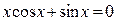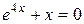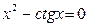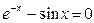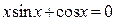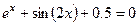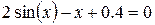Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 1 (25. 07. 13)
ЛАБОРАТОРНАЯ РАБОТА 1 (25.07.13) Решение нелинейных уравнений итерационными методами . Цель работы: научиться решать нелинейные уравнения методом деления пополам, методом простых итераций, средствами пакета MathCAD с помощью ЭВМ. Содержание работы: 1. Изучить методы итераций для решения нелинейных уравнений. 2. На конкретном примере усвоить порядок решения нелинейных уравнений с помощью ЭВМ указанными методами. 3. Составить программу(ы) на любом языке программирования, реализующую(ие) построенные итерационные процессы, используя алгоритмы методов. Печать результатов должен осуществляться на каждом шаге итераций 4. Для заданного варианта решить с помощью программы уравнение с требуемой точностью. Сделать вывод о скорости сходимости методов. 5. Для заданного варианта решить с помощью средств пакета в MathCAD. 6. Составить отчет о работе. Содержание отчета. Отчет по лабораторной работе должен содержать следующие материалы: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы; листинг(и) программ(ы); таблицы результатов (в случае, если число итераций в таблице достаточно большое, в отчет занести две первых и две последних итерации); графический материал ; выводы о работе. Варианты заданий даны в приложении А. Теоретический материал 1. Метод деления пополам Пусть на отрезке Вычисляется точка
Пусть на к-м шаге найден отрезок Тогда на к+1 шаге Алгоритм завершается, если для некоторого к окажется 2. Метод простой итерации. Для построения рабочей формулы уравнение Далее итерационный процесс строится по формуле
Для сходимости итерационного процесса (2) необходимо задать произвольное начальное приближение
Процесс (3) заканчивается при одновременном выполнении двух условий: К виду x=j(x), удобному для итераций, уравнение f(x)=0 можно привести разными способами. Один из способов заключается в следующем. Уравнение x=x+сf(x) Здесь функция 3 Решение уравнения в MathCAD Для решения уравнения вида f(x) = 0 в MathCAD служит функция root. Если f(x) – полином, то вычислить все его корни можно также с помощью функции polyroots. Встроенная функция root в зависимости от типа задачи может иметь либо два аргумента: root (f(x), x), либо четыре аргумента: root (f(x), x, a, b). Здесь f(x) – скалярная функция, определяющая уравнение; x – скалярная переменная, относительно которой решается уравнение; a, b – границы интервала, внутри которого происходит поиск корня. Первый тип функции rootтребует дополнительного задания начального значения переменной x. Для этого нужно просто предварительно присвоить x некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня. Иногда удобнее задавать не начальное приближение к корню, а интервал [a, b], внутри которого корень заведомо находится. В этом случае следует использовать функцию root с четырьмя аргументами, а начальное значение x присваивать не нужно. Поиск корня осуществляется в промежутке между a и b. При этом явный вид функции f(x) может быть определен непосредственно в теле функции root. Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение Эта ошибка может быть вызвана следующими причинами: · Уравнение не имеет корней. · Корни уравнения расположены далеко от начального приближения. · Выражение имеет локальные max и min между начальным приближением и корнями. · Выражение имеет разрывы между начальными приближениями и корнями. · Выражение имеет комплексный корень, но начальное приближение было вещественным. Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет root сходиться. Для нахождения корней алгебраического уравнения, имеющего вид anxn + ... + a2x2 + a1x + a0=0 лучше использовать встроенную функцию polyroots(v), где v – вектор, составленный из коэффициентов полинома. Поскольку полином N-й степени имеет ровно N корней (некоторые из них могут быть кратными), вектор v должен состоять из N+1 элемента. Результатом действия функции polyroots является вектор, составленный из N корней рассматриваемого полинома В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные. Пример решения уравнений средствами Mathcad приведен на рисунке 1.
Рисунок 1.
Задание 1. 1.Локализовать корни уравнения f(x)=0 графически. 2. Методом деления пополам найти с точностью Задание 2. 1. Преобразовать уравнение к виду, удобному для итераций любым способом преобразованием уравнения. Проверить достаточное условие сходимости метода. 2. Найти все корни уравнения с точностью Задание 3. 1. Используя пакет MATHCAD, локализовать корни f(x)=0 графически. 2. Используя встроенную функцию root пакета MATHCAD, найти корни уравнения f(x)=0 с точностью Приложение А № варианта Уравнение № варианта Уравнение
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 5; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.78.184 (0.01 с.) |
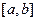 локализован корень уравнения
локализован корень уравнения 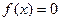 .
.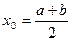 , если
, если 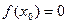 , то
, то 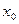 -корень уравнения. Если нет, то из двух половин
-корень уравнения. Если нет, то из двух половин 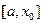 ,
, 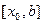 выбирают ту, на концах которой функция имеет противоположные знаки и полагают
выбирают ту, на концах которой функция имеет противоположные знаки и полагают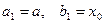 если
если 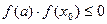
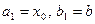 если
если 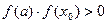 .
.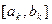 .
.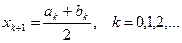
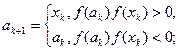
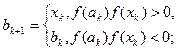 .
.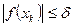 , где
, где 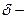 требуемая точность решения. Тогда значение корня
требуемая точность решения. Тогда значение корня 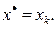 Если задана абсолютная точность определения корня
Если задана абсолютная точность определения корня 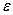 , то алгоритм завершается при условии
, то алгоритм завершается при условии 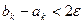 . В этом случае за приближенное значение корня
. В этом случае за приближенное значение корня 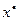 принимается
принимается 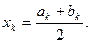
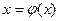 . (1)
. (1) 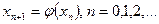 (2)
(2)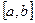 , для которого выполняется условие:
, для которого выполняется условие: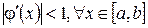 (3)
(3) и
и 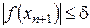 . В этом случае значение
. В этом случае значение 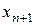 является приближенным значением корня нелинейного уравнения на отрезке
является приближенным значением корня нелинейного уравнения на отрезке 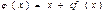 . Тогда
. Тогда 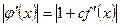 Константа
Константа 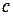 выбирается из условия сходимости (3). Если производная
выбирается из условия сходимости (3). Если производная 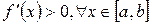 , то значение
, то значение 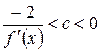 , если производная
, если производная 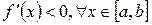 , то – из интервала
, то – из интервала 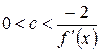 .
. (отсутствует сходимость).
(отсутствует сходимость).
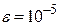 все корни уравнения.
все корни уравнения.