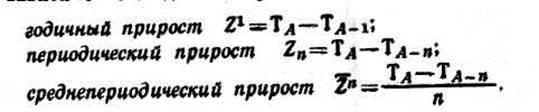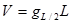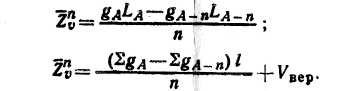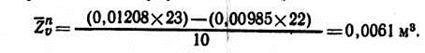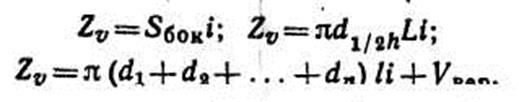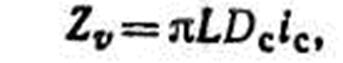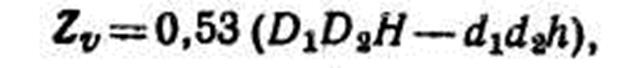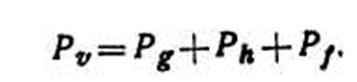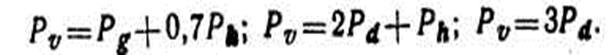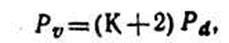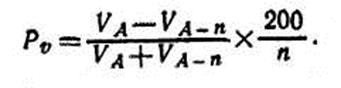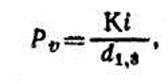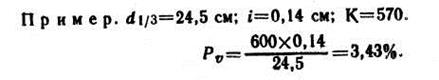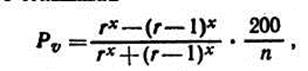Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение текущего прироста отдельного дереваСодержание книги
Поиск на нашем сайте
Задание 5. ОПРЕДЕЛЕНИЕ ПРИРОСТОВ ДРЕВЕСНОГО СТВОЛА (НА СРУБЛЕННОМ ДЕРЕВЕ)
Перед выполнением задания 5 необходимо изучить теоретические положения таксации древесного прироста, изложенные в учебнике «Лесная таксация и лесоустройство» (глава VIII, с. 149—172). Наибольший хозяйственный интерес представляет объемный прирост, т. е. увеличение древесной массы дерева, но это увеличение объема является следствием изменения величины диаметров ствола и соответствующих им площадей сечений (на различных расстояниях от основания), а также следствием изменения высоты и формы (видовых чисел) ствола с возрастом. Поэтому при таксации объемного прироста приходится определять и прирост по этим перечисленным показателям. В лесной таксации известны два вида древесного прироста по каждому показателю: средний и текущий. Средним приростом называют величину, на которую в среднем за 1 год на протяжении всей жизни дерева (или насаждения) изменяется абсолютная величина таксационного показателя. Определяют средний прирост делением таксационного показателя на возраст дерева. Текущий прирост — это величина, на которую изменился таксационный показатель за один конкретный год жизни дерева, например за последний год. Определяют текущий прирост как разность в величине таксационных показателей в данный момент и год назад. Так как разница в показателях, вызванная деятельностью камбия за 1 год, невелика и трудно поддается точному инструментальному измерению, текущий прирост определяют чаще всего по разности показателей, установленной не за 1 год, а за некоторый период, например за 5 или 10 лет. Эта последняя разница будет периодическим приростом по тому или иному показателю. Если разделить периодический прирост на число лет во взятом периоде, тополучают средний годичный прирост в интересующем таксатора периоде. Этот средний годичный прирост в определенном периоде хотя и не является текущим, приростом в буквальном смысле слова, но позволяет судить о текущем годичном приросте того или иного показателя в последний год жизни. Текущие и средние приросты вычисляют, в абсолютных единицах по следующим формулам:
где ZT — приравненный к текущему средний годичный прирост по таксационному показателю Т (диаметр, высота, площадь сечения, объем) за последние n лет; Δг — средний прирост по показателю Т за всю жизнь дерева; ТА — значение показателя Т в возрасте дерева А; ТA-n—значение показателя Тn лет назад. Иногда необходимо иметь представление об относительной величине прироста. В таких случаях вычисляют процент текущего прироста Р (по интересующим таксатора показателям), используя формулу
Студенты, выполняя задание 5, вычисляют средний и текущий (среднепериодический годичный) приросты, а также проценты текущего прироста: 1) по диаметру на высоте 1,3 м от основания, 2) по площади сечения на этой же высоте, 3) по высоте дерева и 4) по его объему (без коры). Исходными данными задания служат показатели обмера срубленных модельных (или учетных) деревьев, использованные частично при выполнении заданий 1—4. Эти данные приведены в приложении 1 в конце книги. В качестве исходных данных можно также использовать заполненные карточки модельных деревьев, срубленных на учебной практике учащимися предыдущих курсов или взятых таксаторами при лесоустройстве лесничества. Определение приростов и процентов прироста по диаметру, высоте и площади сечения весьма несложно по содержанию: оно требует подстановки конкретных значений D, Н и q из исходных данных в выше приведенные формулы. Определение приростов по объему несколько сложнее: предварительно надо найти объем современного ствола VА и объем ствола VA-10, который был 10 лет назад. Нахождение объема современного ствола ведется по сложной формуле срединных сечений. Значение VА уже было определено в задании 1. Для определения VA-10 надо сначала найти на серединах двухметровых отрезков диаметры, которые были 10 лет назад. Для этого из значений диаметров в настоящее время (без коры) вычитают приросты по диаметру, указанные в исходных данных. Следует помнить, что число полных двухметровых отрезков на стволе, которое было 10 лет назад, может быть меньше, чем на современном стволе. Определив диаметры на серединах отрезков и у основания вершинки, находят площади сечений (используя справочные пособия, где есть таблицы площадей кругов) и сами объемы сначала отрезков и вершинки, а затем и всего ствола, который был 10 лет назад. После этого по приведенным выше формулам прироста находят средний и текущий объемный прирост (в абсолютных величинах), а также процент объемного прироста.
Пример выполнения задания 5 Исходные данные: 1. Основные параметры срубленного дерева: Порода —ель. Высота современного ствола—25,9 м. Высота ствола 10 лет назад—24,6 м. Диаметр на высоте 1,3 м, см — 28,2 / 25,3 (в коре / без коры). Возраст дерева — 92 года. Диаметр ствола без коры на высоте 1,3 м 10 лет назад — 23,3 см. Прирост по диаметру за последние 10 лет, см — 2,0. Число годичных слоев (N1,3) на срезе на высоте 1,3 м — 82. 2. Данные детального обмера диаметров и их периодических приростов даны в табл. 9. 3. Определение приростов срубленного дерева выполняют по следующим формулам: а) по высоте:
б) по диаметру на высоте 1,3 м
№ двухметровых отрезов Расстояние середины отреза от основания ствола, м Диаметр на середине отреза без коры, см Прирост по диаметру за 10 лет, см Диаметр на середине отреза 10 лет назад, см Объемы о трезов, м3 в момент таксации 10 лет назад ч 25,6 2,0 23,6 0,0875 24,8 2,2 22,6 0,0966 0,0802 24,1 2,4 21,7 0,0912 0,0740 23,4 2,5 20,9 0,0860 0,0686 22,4 2,5 19,9 0,0788 0,0622 21,9 2,4 19,5 0,0753 0,0597 20,7 2,6 18,1 0,0673 0,0515 19,3 2,5 16,8 0,0585 0,0443 17,6 2,8 14,8 0,0487 0,0344 16,0 3,6 13,4 0,0402 0,0282 13,9 4,2 9,7 0,0303 0,0148 9,0 5,0 4,0 0,0127 0,0025 Вершинка (основание) 6,1 5,0 1,1 0,0018 —
Общий объем ствола 0,7904 0,6079 в) по площади сечения на высоте 1,3 м:
г) по объему:
В процессе роста дерева, под влиянием происходящих в нем различных физиологических процессов: фотосинтеза, дыхания, водообмена и обмена питательных веществ, происходит увеличение размеров в высоту (из точки роста, находящейся в верхушечной почке последнего годичного побега) и толщину (вследствие деления клеток камбиального слоя). В результате этого увеличиваются площадь сечения и объем дерева. Это увеличение и называется приростом. Различают средний (Δ) и текущий (Z) приросты дерева. Средний прирост характеризует величину изменения таксационного показателя в среднем в единицу времени в течение всей жизни дерева Δ=Т/А. Текущий прирост есть величина, на которую изменяется таксационный показатель за определенный период (n лет) жизни дерева. Он определяется как разность в величине таксационного показателя в возрасте А и А — n лет. В зависимости от длины периода n лет различают:
Вследствие малой (трудноизмеримой) величины годичного прироста и его большой изменчивости по годам последний вид прироста на практике определяют наиболее часто, принимая за n период в 3, 5 или 10 лет. У срубленного дерева величина текущего прироста по высоте и диаметру может быть определена непосредственным измерением, а по площади сечения и объему — путем расчетов. Известно множество способов определения объемного прироста. Наиболее полная их сводка дана в монографии В. В. Антанайтиса и В. В. Загреева «Прирост леса [18]. В отечественной практике наиболее часто для определения объемов срубленных на пробных площадях модельных (учетных) деревьев используют простую или сложную формулы срединных сечений (формулы Губера):
V = (g1+ g2+ g3+…+gn)*L+Vверш где V — объем ствола; g1/2 — площадь сечения ствола на середине его длины; L — длина ствола; g1 g2, g3, gn — срединные площади сечений отдельных и равных по длине отрезков ствола; / — длина отрезков; VBep — объем вершинки ствола. Тогда среднепериодическйй прирост по объему ствола за n лет будет равен:
Задача. Определить прирост по объему срубленного ствола длиной 23 м по простой формуле срединного сечения. Решение. Путем постепенного отрубания вершины ствола и подсчета числа годичных колец на месте отруба находим прирост в высоту, например, за последние 10 лет. Допустим, что он оказался равным 1,0 м. Путем измерения определяем диаметры на половине длины ствола в возрасте А лет (11,5 м) в коре — 13,0 см, без коры — 12,4 см и в возрасте А — n лет (11,0 м) в коре — 13,3 см, без коры — 12,7 см. С помощью приростного бурава или на зарубе, сделанном на половине длины ствола в возрасте А — n лет (11,0 м), определяем прирост по радиусу за последние 10 лет — 0,75 см. Вычитая удвоенную величину радиального прироста (прирост по диаметру) из диаметра без коры, получаем диаметр на половине длины ствола в возрасте А — n лет (без коры dА-n= 12,7—1,5= 11,2 см). По таблице находим площади поперечных сечений, соответствующие срединным диаметрам без коры в возрасте А лет — 0,01208 ма и А — n лет — 0,00985 м2. Подставляя полученные данные в приведенную выше формулу, определяем среднепериодический прирост по объему:
Точность определения объемного прироста этим способом невысока и колеблется в пределах ±12—20 %. Она значительно повышается (до ±3— 5 %), если объемы стволов в возрасте А и А — n лет определяют по сложной формуле срединных сечений. С меньшими трудозатратами, но и некоторой потерей точности Zv срубленного дерева можно определить одним из следующих упрощенных способов: 1. По площади боковой поверхности ствола (по А. В. Тюрину):
где Sбок — площадь боковой поверхности ствола; d1/2h— диаметр на середине длины ствола; d1 d2 — диаметры на середине отдельных отрезков; i — ширина годичного слоя (радиальный прирост). 2. По формуле М. Л. Дворецкого
где Dc — средний из срединных диаметров двухметровых отрезков; iс –средняя ширина годичного слоя на высотах 1,3 м, 1/2h и l/4h 3. По формуле Б. А. Шустова
где D1, d1— диаметры на высоте 1,3 м без коры в возрасте А и А — n лет; D2, d2 — диаметры на половине длины ствола без коры в возрасте А и А — n лет; Н, h — длина ствола в возрасте А и А — n лет. Для сравнительной оценки текущего прироста отдельных деревьев чаще используют не абсолютные значения прироста, а их проценты (Р). Процент среднепериодического текущего прироста по объему (Pv) срубленного дерева есть сумма процентов прироста по площади сечения, высоте и видовому числу:
Приближенные значения процентов прироста дают формулы
С целью некоторого их уточнения Г. М. Турский предложил формулу
где значение К меняется в зависимости от энергии роста в высоту в пределах от 0 до 1,3: для деревьев, прекративших рост в высоту, К=0, имеющих слабый рост — 0,4, умеренный — 0,7, хороший — 1,0 и очень хороший — 1,3. На практике наиболее часто процент прироста по объему определяют по формуле Пресслера
У растущих деревьев прирост по высоте Zh не может быть установлен прямым измерением, а величину радиального прироста Zr можно измерить лишь на высоте, близкой к высоте 1,3 м. Поэтому прирост по объему определяют путем внесения в расчетные формулы поправочных коэффициентов, учитывающих энергию роста в высоту и характер изменения ширины годичного слоя по длине ствола, либо путем установления прямых связей объемного прироста с приростом по диаметру или площади сечения. Чаще всего объемный прирост растущих деревьев определяется через процент прироста одним из следующих способов: 1. По приведенным выше формулам связи Pv с Рd. 2. По формуле Шнейдера
где К — коэффициент, определяемый по приведенной ниже таблице в зависимости от длины кроны и энергии роста в высоту; i — средняя за n лет ширина годичного слоя; d1,3 — диаметр на высоте груди без коры в возрасте А — n лет. Коэффициент К Начало кроны Рост в высоту прекратился слабый умеренный хороший очень хороший превосходный Ниже1/2h Между 1/2h и 3/4h Выше 3/4h
3. По формуле М. Преслера
где r — относительный диаметр, определяемый по формуле r•=d1,3/Zd — показатель степени, характеризующий рост дерева в высоту и изменяющийся в пределах от 2 до 3,5. Расчеты упрощаются при пользовании таблицей 141. 141. Прирост по объему стволов, %, растущих деревьев Относи-тельный диаметр Прирост за n лет при росте в высоту по группам Относи-тельный диаметр Прирост за n лет при росте в высоту по группам II III IV V II III IV V 7,9 9,0 7,4 8,5 9,5 7,0 7,9 8,9 6,5 7,5 8,4 9,5 6,2 7,1 8,0 8,9 5,9 6,8 7,6 8,5 5,6 6,4 7,2 8,0 5,4 6,1 6,9 7,8 5,1 5,9 6,6 7,4 4,9 5,6 6,3 7,0 4,7 5,4 6,1 6,8 4,6 5,2 5,9 6,5 4,4 5,1 5,7 6,3 4,3 4,9 5,5 6,1 4,2 4,7 5,3 5,9 4,0 4,5 5,1 5,7 3,7 4,2 4,7 5,3 3,5 3,9 4,4 4,9 3,3 3,7 4,2 4,6 3,2 3,6 4,0 4,4 2,9 3,4 3,8 4,1 9,1 2,6 3,0 3,4 3,8 8,5 9,7 2,3 2,7 3,0 3,4
Выбор группы роста производится в зависимости от высоты, с которой начинается крона дерева, и энергии роста в высоту по следующей вспомогательной таблице Начало кроны Рост в высоту слабый умеренный хороший Ниже1/2h II III IV Между 1/2h и 3/4h II,5 III,5 IV,5 Выше 3/4h III IV V Пример. Определить среднепериодический (за 10 лет) прирост по объему растущего дерева в %, если D1,3=24,5 cm, Zd=2,7 см, r=24,5/2,7= =9,0, крона расположена выше 3/4 h, рост в высоту — умеренный. По вспомогательной таблице находим, что это IV группа роста. Тогда по таблице 141 Рv=35% за 10 лет и Рv = 3,5% в год.
|
||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 48; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

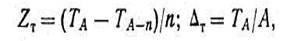
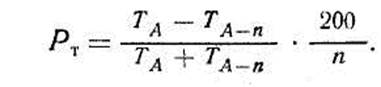
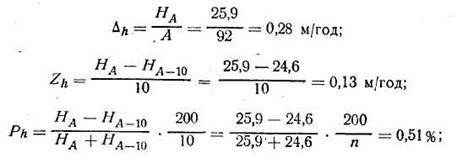
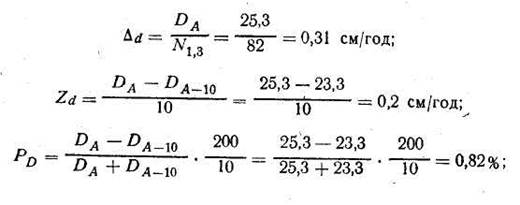
 9. Детальный обмер диаметров и их приростов
9. Детальный обмер диаметров и их приростов