Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первообразная и неопределенный интегралСодержание книги
Поиск на нашем сайте
Первообразная и неопределенный интеграл Определение. Непрерывная функция F(x) называется первообразной функции f(x), если на промежутке X, если для каждого Операция нахождения первообразной функции f(x), называется интегрированием. Неопределенный интеграл Неопределённый интеграл- это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:
где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования. Дифференциал- произвольное, бесконечно малое приращение переменной величины.
2.Свойства неопределенного интеграла, таблица основных интегралов Свойства неопределённого интеграла
Таблица основных неопределённых интегралов В виде
где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования.
Метод замены переменных
Интегрирование по частям
Разложение рациональных дробей на элементарные дроби
Интегрирование рациональных дробей Алгоритм интегрирования рациональной дроби 1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:
2. Знаменатель разложим на простейшие сомножители: Qn(x)
3. Представим дробь
виде суммы простейших дробей с неопределенными коэффициентами.
4. Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства. 5. Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях x.
6. Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая равным действительным корням знаменателя. 7. Подставим найденные коэффициенты A1,A2,…,Cs,Ds в разложение дроби. 8. Проинтегрируем простейшие дроби. Интегрирование тригонометрических функций
Интегралов Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где) называется приращение какой-нибудь её первообразной на этом отрезке. · Определённый интеграл с одинаковыми пределами интегрирования равен нулю · Величина определённого интеграла не зависит от обозначения переменной интегрирования · Постоянный множитель можно выносить за знак определённого интеграла · Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов · Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям · При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак · Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке x0 внутри его · Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен) · Если верхний предел интегрирования больше нижнего и функции f(x) и g(x) непрерывны, то неравенство f(x) >=g(x) можно почленно интегрировать Теорема. Если функция f(x) интегрируема на отрезке [ a, b ], где a < b, и для всех x ∈ [a, b] выполняется неравенство
то
С помощью неравенств из теоремы можно оценить определенный интеграл, т.е. указать границы, между которыми заключено его значение. Эти неравенства выражают оценку определенного интеграла. Теорема [Теорема о среднем]. Если функция f(x) интегрируема на отрезке [ a, b ] и для всех x ∈ [a, b] выполняются неравенства m ≤ f(x) ≤ M, то
где m ≤ μ ≤ M. Замечание. В случае, когда функция f(x) непрерывна на отрезке [ a, b ], равенство из теоремы принимает вид
где c ∈ [a,b]. Число μ=f(c), определяемое данной формулой, называется средним значением функции f(x) на отрезке [ a, b ]. Это равенство имеет следующий геометрический смысл: площадь криволинейной трапеции, ограниченной непрерывной линией y=f(x) (f(x) ≤ 0), равна площади прямоугольника с тем же основанием и высотой, равной ординате некоторой точки этой линии.
Формула Ньютона--Лейбница Поскольку любые две первообразные функции f(x) отличаются на постоянную, то согласно предыдущей теореме можно утверждать, что любая первообразная Φ(x) непрерывной на сегменте [ a, b ] функции f(x) имеет вид
где C - некоторая постоянная. Полагая в этой формуле x=a и x=b, используя св.1 определенных интегралов, найдем
Из этих равенств вытекает соотношение
Таким образом доказали следующую теорему: Теорема. Определенный интеграл от непрерывной функции равен разности значений любой ее первообразной для верхнего и нижнего предела интегрирования. Формулу Ньютона-Лейбница можно переписать в виде
где
Первообразная и неопределенный интеграл Определение. Непрерывная функция F(x) называется первообразной функции f(x), если на промежутке X, если для каждого Операция нахождения первообразной функции f(x), называется интегрированием. Неопределенный интеграл Неопределённый интеграл- это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:
где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования. Дифференциал- произвольное, бесконечно малое приращение переменной величины.
2.Свойства неопределенного интеграла, таблица основных интегралов
|
||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 52; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.248.140 (0.008 с.) |

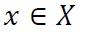
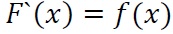 .
.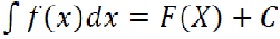 ,
,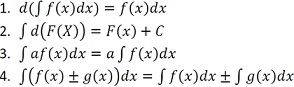
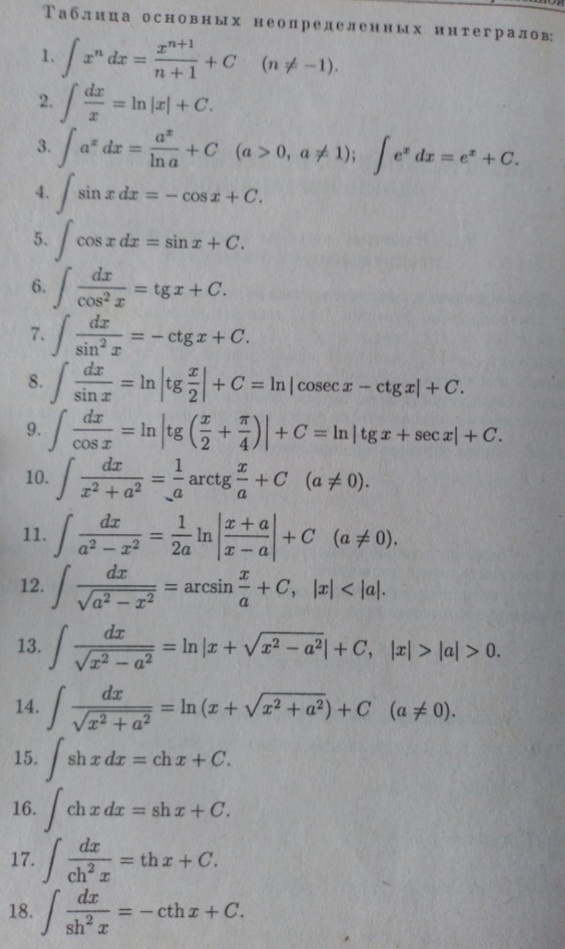



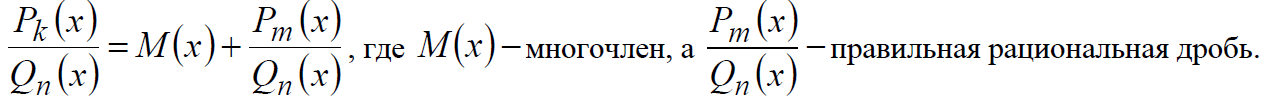
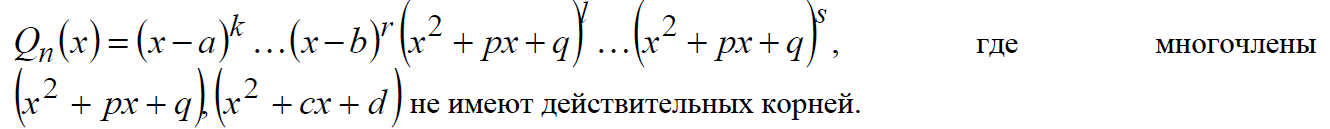
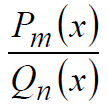
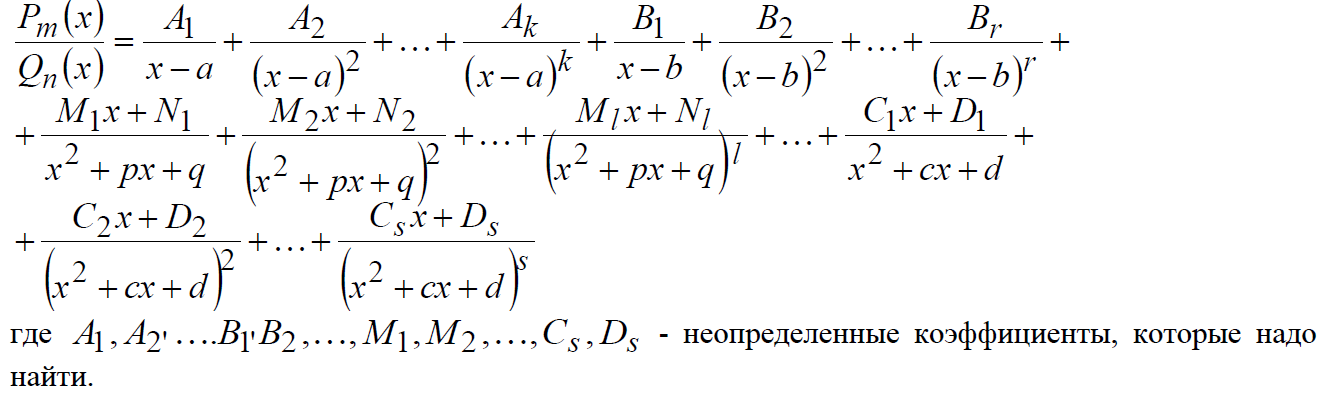

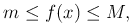
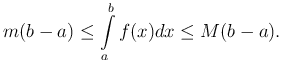
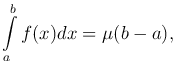
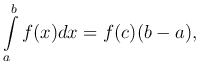
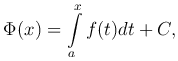
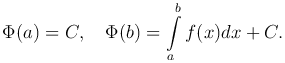
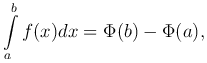 которое называется формулой Ньютона-Лейбница.
которое называется формулой Ньютона-Лейбница.