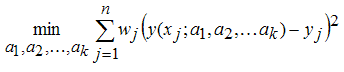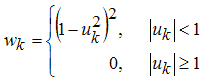Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опции, управляющие процессом подбора параметровСодержание книги
Поиск на нашем сайте
Для задания опций вычислительных алгоритмов, использующихся для подбора параметров служит кнопка < Fit options> диалогового окна Fitting. После нажатия на эту кнопку появляется диалоговое окно, в заголовке которого написано Fit options for и далее указано имя параметрической модели. В зависимости от типа выбранной параметрической модели состав этого окна может быть различным. Для сплайновой интерполяции и сглаживающего сплайна это окно не содержит никаких элементов управления, поскольку дополнительных опций соответствующие алгоритмы не требуют. Для линейных моделей можно задавать выбор целевой функции (об этом написано чуть ниже) и границы для искомых коэффициентов. Для других типов параметрических моделей диалоговое окно Fit options for выглядит следующим образом (Рис. 23)
по умолчанию они считаются равными единице).
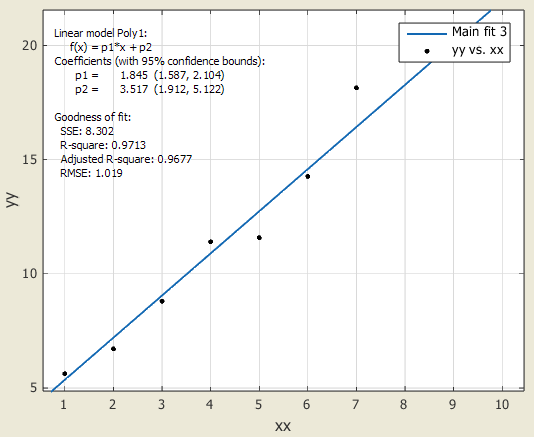
Если имеется выброс в данных, причем соответствующий вес не задан достаточно маленьким, то он может существенно ухудшить приближение, например на следующем графике (Рис. 24) приведены данные с одним выбросом, приближаемые полиномом первой степени (линейная регрессия). Данные без выброса сгенерированы следующим образом >> xx=1:10; >> yy=2*xx+3+randn(size(xx)); Коэффициенты линейной функции находятся из условия минимума суммы квадратов невязок, все веса равны единице.
Рис. 24 Результат приближения данных, при отсутствии явных выбросов
Выброс в девятой точке равный нулю сделаем переприсвоением значения элемента массива
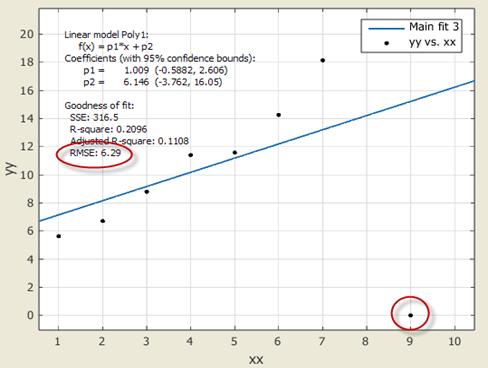
>> yy(9)=0; При этом не будем указывать вес этой точке. Выброс оказывает такое сильное влияние (Рис. 25), поскольку невязка в минимизируемом выражении возводится в квадрат.
Рис. 25 Результат приближения данных, при наличии явного выброса в режиме минимизации суммы квадратов невязок (Off)
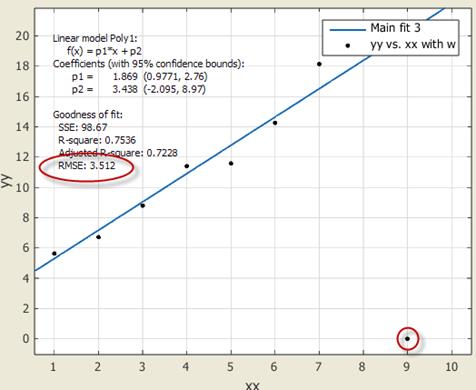
Одним из способов уменьшения влияния выбросов на качество получаемого приближения состоит в минимизации суммы не квадратов невязок, а их модулей. Для этого служит опция LAR (least absolute residuals). После выбора LAR в раскрывающемся списке Robust диалогового окна Fit options и снова провести линейную регрессию, то мы увидим, что выброс в данных намного меньше влияет на получающееся приближение линейной функцией (Рис. 26). С другими типами параметрических моделей дело будет обстоять аналогичным образом.
Рис. 26 Результат приближения данных, при наличии явного выброса в режиме минимизации суммы квадратов модулей невязок (LAR)
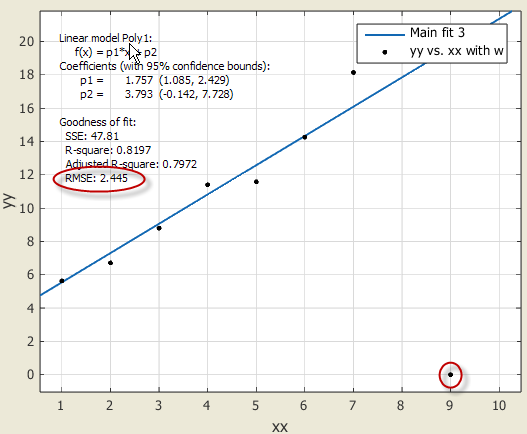
Зададим веса всем данным равные единице, кроме выброса, а для выброса установим вес 0.1: >> w=ones(size(xx)); >> w(9)=0.1; Снова приблизим данные линейной параметрической моделью, только теперь следует импортировать их заново в приложение cftool, нажав кнопку Data в основном окне приложения и выбрав массивы xx, yx и w в раскрывающихся списках X Data, Y Data и Weights, соответственно. Перед началом подбора параметров выберем метод наименьших квадратов, для чего следует нажать кнопку Fit options и установить опцию Off в раскрывающемся списке Robust. Получающееся приближение приведено на Рис. 27. Заметно, что выброс практически не оказывает влияния на приближение.
Рис. 27 Результат приближения данных с выбросом линейной моделью по методу наименьших квадратов с весами. Выброс имеет маленький вес по сравнению с весами для остальных данных.
В этом примере можно было назначить точке, в которой есть заметный выброс, нулевой вес, или же воспользоваться предварительной обработкой данных для исключения выбросов (см. раздел Предварительная обработка данных). Однако, в практических задачах не всегда удается так просто определить выбросы или точки данных, которые должны оказывать меньшее влияние на получающееся приближение и назначить им соответствующие веса. Вместо этого можно воспользоваться адаптивным алгоритмом, который последовательно:
1. делает приближение, подбирая параметры по методу наименьших квадратов; 2. вычисляются приведенные невязки (см. более подробно в справочной системе по Curve Fitting Toolbox раздел Fitting Data: Parametric Fitting: The Least Squares Fitting Method); 3. в зависимости от удаленности точек от приближающей их кривой данным назначаются веса по следующему правилу (чем дальше точка, тем меньше ее вес):
4. если веса достаточно сильно изменились, то переходим к п. 1), а если процесс сошелся, то останавливаем алгоритм, нужное приближение построено. Поскольку в приведенном выше адаптивном алгоритме присутствует четвертая степень невязки, то он называется Bisquare weights (биквадратные веса). Для выбора такого способа приближения параметрической моделью следует установить опцию Bisquare в раскрывающемся списке Robust диалогового окна Fit options. Разумеется, если пользователь задал данные и некоторые начальные веса, то они изменятся. Результирующий вес для каждой точки будет являться произведением исходного веса на тот, который вычисляет алгоритм Bisquare weights. Результат приближения данных с выбросом линейной параметрической моделью при помощи алгоритма Bisquare weights с автоматическим подбором весов для уменьшения влияния выбросов в данных на получаемое приближение приведен на Рис. 28.
Рис. 27 Результат приближения данных с выбросом линейной моделью по методу наименьших квадратов адаптивным алгоритмом (Bisquare).
Следующие опции в диалоговом окне Fit options служат для настройки алгоритмов минимизации целевой функции (в общем случае взвешенной суммы квадратов или модулей невязки. MaxFunEvals - максимальное количество вычислений минимизируемой функции (для предотвращения зацикливания), по умолчанию минимизируемая функция вычисляется не более 600 раз, после чего алгоритм минимизации останавливается.
MaxIter - максимальное число итераций алгоритма минимизации (для предотвращения зацикливания), по умолчанию делается не более 400 итераций, после чего алгоритм минимизации останавливается.
TolFun - точность по функции (для завершения итерационного алгоритма), по умолчанию 1.0Е-6, при достижении этой точности алгоритм минимизации останавливается.
TolX - точность по искомым параметрам (для завершения итерационного алгоритма), по умолчанию 1.0Е-6, при достижении этой точности алгоритм минимизации останавливается.
DiffMinChange - минимальный шаг по каждой из искомых переменных (параметров модели) для вычисления приближенного вычисления частных производных (используемых в алгоритмах минимизации) при помощи конечных разностей, по умолчанию 1.0Е-8.
DiffMaxChange - минимальный шаг по каждой из искомых переменных (параметров модели) для вычисления приближенного вычисления частных производных (используемых в алгоритмах минимизации) при помощи конечных разностей, по умолчанию 0.1.
В диалоговом окне Fit options также можно задавать границы для разыскиваемых параметров параметрической модели и начальные приближения. Для стандартных и пользовательских параметрических моделей предлагаются по умолчанию (там где это нужно, в зависимости от типа параметрической модели) следующие границы параметров и начальные приближения.
|
||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 61; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.207.209 (0.01 с.) |

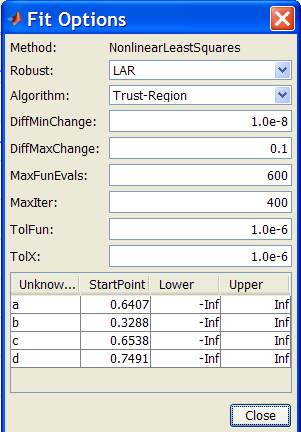 Рис. 23 Диалоговое окно Fit options
для задания опций
вычислительных алгоритмов
Рис. 23 Диалоговое окно Fit options
для задания опций
вычислительных алгоритмов
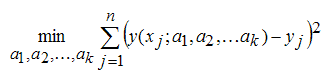 Если данные (xj,yj) j=1,2,...,n снабжены весами (wj) j=1,2,...,n то решается следующая задача минимизации (если веса не заданы, то
Если данные (xj,yj) j=1,2,...,n снабжены весами (wj) j=1,2,...,n то решается следующая задача минимизации (если веса не заданы, то