

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Эдс при движении проводника в магнитном поле.

| Явление самоиндукции
| | Явление самоиндукции - частный случай электромагнитной индукции и, следовательно, для него справедливы все закономерности явления электромагнитной индукции. При этом
1. Изменяющееся магнитное поле индуцирует ЭДСиндукции в том же самом проводнике, по которому течет ток, создающий это поле.
2. Вихревое магнитное поле препятствует нарастанию тока в проводнике.
3. При уменьшении тока вихревое поле поддерживает его.
| | | Если через катушку пропускать ток, то Ф ~ I. Следовательно, Ф=LI, где L — индуктивность катушки (коэффициент самоиндукции), характеризующая ее магнитные свойства.
| | Согласно закону электромагнитной индукции  Но ΔФ=LΔI, следовательно:
Но ΔФ=LΔI, следовательно: 
| | | Энергия магнитного поля.
| По аналогии с кинетической энергией: 
| | | КОЛЕБАНИЯ
|
| | Колебания – процессы (изменения состояния), обладающие той или иной повторяемостью во времени.
Механические колебания – движения, которые точно или приблизительно повторяются во времени.
| | Период Т — время, за которое совершается одно полное колебание. Выражается в секундах (с).  Частота — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц). Частота — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц).
 
Циклической (круговой) частотой периодических колебаний наз. число полных колебаний, которые совершаются за 2 единиц времени (секунд). Единица измерения – с-1.

Фаза колебания - j - физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад).
Ф аза колебания в начальный момент времени (t=0) называется начальной фазой (j0).

Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями.
 
Фаза колебания:  скорость – это производная от координаты по времени скорость – это производная от координаты по времени 
Величина  - максимальная скорость колебательного движения - максимальная скорость колебательного движения
для скорости при гармоническом колебании имеем:  , ,
а для случая нулевой начальной фазы 

ускорение – это производная от скорости по времени:
 - -
для ускорения имеем:  ,а для случая нулевой начальной фазы: ,а для случая нулевой начальной фазы: 
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити (физическая модель).

| Колебания пружинного маятника.
| | | В вертикальном положении на груз на пружине действуют сила тяжести и сила упругости пружины. Под действием силы тяжести пружина растягивается на х1, а затем мы отклоняем его от этого положения на х.
| |

| | | | Волна — распространяющиеся колебания.
Волнами называются всякие возмущения состояния вещества или поля, распространяющиеся в пространстве с течением времени.
| | | Основное свойство волны — перенос энергии без переноса вещества.
| | | Виды волновых процессов:
1. Механические волны (см. рисунки):
а) упругие.
б) поверхностные (под действием сил тяжести и поверхностного натяжения).
2. Электромагнитные волны (колебания векторов напряженности электрического и индукции магнитного полей, распространяющиеся в пространстве). В отличие от механических, могут распространяться в вакууме.
| | Основные характеристики волны.

| Интерференция волн
| | Явление интерференции возникает при наложении когерентных волн.
Когерентные волны - это волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
| Постоянное во времени явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн называется интерференцией. В результате в пространстве образуется устойчивая картина чередования областей усиленных и ослабленных колебаний.
Условиe максимума

Условие минимума
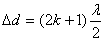
| ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
|
| | Периодические изменения во времени электрического заряда (силы тока, напряжения) называются электромагнитными колебаниями.
Электрическая цепь, состоящая из последовательно соединенных конденсатора с емкостью C и катушки с индуктивностью L, наз. колебательным контуром.
| 
| Уравнение гармонического колебания заряда (изменение величины электрического заряда!):  . .
Колебания тока:  , т.о. , т.о. 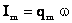 . .
Для энергии электрического поля конденсатора воспользуемся выражением  , ,
а для энергии магнитного поля катушки  . .

 - формула Томсона - формула Томсона
з закона сохранения энергии следует: 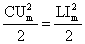 и, и,
следовательно, 
| Емкостное сопротивление в цепи переменного тока
| | При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ¹ 0. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока.
| 
| Мгновенное значение напряжения равно  .
Мгновенное значение силы тока равно: .
Мгновенное значение силы тока равно:  Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.
Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.
| 
| Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим:  ,
где ,
где  - емкостное сопротивление. - емкостное сопротивление.
| 
| | Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты).
| 
| | Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току).
| 
| | Индуктивное сопротивление в цепи переменного тока
| | | В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения.
| 
| | Мгновенное значение силы тока: 
| 
| | 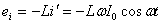 .
Следовательно .
Следовательно  где
где  амплитуда напряжения.
Напряжение опережает ток по фазе на p /2. амплитуда напряжения.
Напряжение опережает ток по фазе на p /2.
| 
| | | Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину wL за сопротивление катушки переменному току, получим: - закон Ома для цепи с чисто индуктивной нагрузкой.
| 
| | Величина  - индуктивное сопротивление. - индуктивное сопротивление.
| 
| | | Закон Ома для полной цепи переменного тока.
| 
| | Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения.
В этом случае: 
 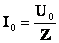 - полное сопротивление переменному току.
- полное сопротивление переменному току.
| 
| | Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим:  .
.
| 
| | | Мощность в цепи переменного тока.
| | Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): 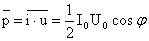
| 
| | или, переходя к действующим значениям,  . .
| 
| | | Трансформатор
|
| | | Преобразует переменный ток: изменяются напряжение и сила тока, не изменяются мощность и частота I2.
| | | | | | | | | | | | |  
| Эффект трансформации возникает из-за неодинакового количества витков в первичной и вторичной обмотках!
| k> 1 - понижающий
k< 1 - повышающий
| . Работа под нагрузкой
 При включении во вторичную цепь нагрузки R в ней возникает ток I2 той же частоты, что и ток I1. Напряжение во вторичной цепи При включении во вторичную цепь нагрузки R в ней возникает ток I2 той же частоты, что и ток I1. Напряжение во вторичной цепи  . Т.к. участки нагрузки присоединяются ко вторичной обмотке трансформатора параллельно, то при увеличении нагрузки сопротивление уменьшается, а сила тока согласно закону Ома увеличивается. Значит, напряжение на нагрузке уменьшается. . Т.к. участки нагрузки присоединяются ко вторичной обмотке трансформатора параллельно, то при увеличении нагрузки сопротивление уменьшается, а сила тока согласно закону Ома увеличивается. Значит, напряжение на нагрузке уменьшается.
|




 Но ΔФ=LΔI, следовательно:
Но ΔФ=LΔI, следовательно: 

 Частота — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц).
Частота — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц).





 скорость – это производная от координаты по времени
скорость – это производная от координаты по времени 
 - максимальная скорость колебательного движения
- максимальная скорость колебательного движения ,
,

 -
- ,а для случая нулевой начальной фазы:
,а для случая нулевой начальной фазы: 




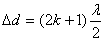

 .
. , т.о.
, т.о. 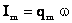 .
. ,
, .
.
 - формула Томсона
- формула Томсона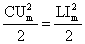 и,
и,

 .
Мгновенное значение силы тока равно:
.
Мгновенное значение силы тока равно:  Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.
Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.

 ,
где
,
где  - емкостное сопротивление.
- емкостное сопротивление.




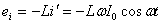 .
Следовательно
.
Следовательно  где
где  амплитуда напряжения.
Напряжение опережает ток по фазе на p /2.
амплитуда напряжения.
Напряжение опережает ток по фазе на p /2.

 - индуктивное сопротивление.
- индуктивное сопротивление.



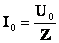 - полное сопротивление переменному току.
- полное сопротивление переменному току.

 .
.

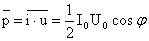

 .
.


 При включении во вторичную цепь нагрузки R в ней возникает ток I2 той же частоты, что и ток I1. Напряжение во вторичной цепи
При включении во вторичную цепь нагрузки R в ней возникает ток I2 той же частоты, что и ток I1. Напряжение во вторичной цепи  . Т.к. участки нагрузки присоединяются ко вторичной обмотке трансформатора параллельно, то при увеличении нагрузки сопротивление уменьшается, а сила тока согласно закону Ома увеличивается. Значит, напряжение на нагрузке уменьшается.
. Т.к. участки нагрузки присоединяются ко вторичной обмотке трансформатора параллельно, то при увеличении нагрузки сопротивление уменьшается, а сила тока согласно закону Ома увеличивается. Значит, напряжение на нагрузке уменьшается.


