Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розподіл грошового місячного доходу домогосподарств
Середня величина характеризує типовий рівень ознаки в сукупності. Для незгурпованих даних середня розраховується за формулою середньої аріфметичної простої:
де N – кількість одиниць сукупності.
За згрупованими даними ряду розподілу середня розраховується як арифметична зважена:
де n - число груп xi` - середина інтервалу.
Це значення показує, що при рівномірному розподілі суми місячного доходу по домогосподарствах величина доходу кожного дорівнювала би 469,4 ден.ед.
2.
Рис. 1.1. Полігон і гістограма розподілу домогосподарств по величині місячного доходу
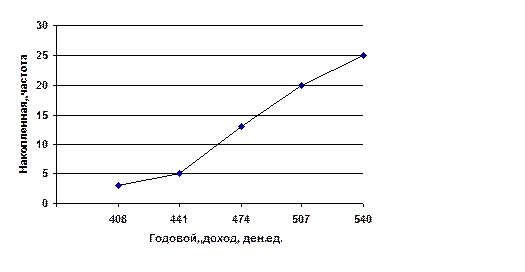
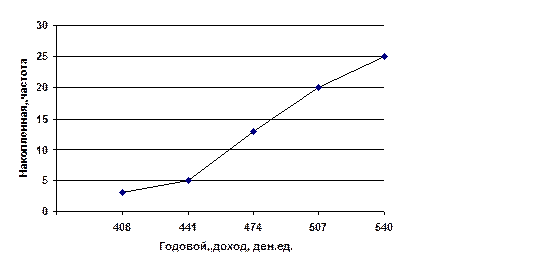
Рис. 1.2. Кумулята грошового доходу
Визначимо характеристики центру розподілу. До показників центру розподілу відносяться середня арифметична, мода і медіана, які використовуються для характеристики середнього значення ознаки у варіаційному ряду. Середня величина характеризує типовий рівень ознаки в сукупності. За даними ряду розподілу середня була розрахована як арифметична зважена: Мода - це значення ознаки, що найбільш часто зустрічається, тобто варіанту, яка у ряді розподілу має найбільшу частоту (частість). У дискретному ряду мода визначається візуально по максимальній частоті, або частості. У інтервальному ряду мода визначається в межах модального інтервалу за ознакою
де Хмо - початок модального інтервалу; і - розмір інтервалу; fМо, fМо-1, fМо+1 - частота відповідно модальному, передмодальному і наступного за модальним інтервалам. Модальний інтервал, в якому Мо = 441 + 33х (8-2)/((8-2) + (8-7)) = 469,3 ден.ед. В даному випадку найпоширенішим розміром доходу домогосподарства за місяць умовно є 469,3 ден.ед.
Медіана - це варіанта, яка розташована у середині впорядкованого ряду розподілу і ділить його навпіл на дві рівні за об'ємом частини. Медіана, як і мода, не залежить від крайніх значень варіант, тому використовується для характеристики центру розподілу з невизначеними межами. У дискретному ряду розподілу медіаною буде перше з початку ряду значення ознаки, для якої кумулятивна частота Si перевищує половину об'єму сукупності. У інтервальному ряду таким самим чином, за кумулятивною частотою, визначається медіанний інтервал:
де Хме - нижня межа медіанного інтервалу; і - розмір інтервалу; fi - частоти; fМе - частота медіанного інтервалу; Sме-1 - накопичена частота інтервалу, передуючого медіанному. Медіанний інтервал з умови Ме = 441 + 33 х (12,5-5) /8 = 471,9 ден.ед. Це означає, що половина домогосподарств має дохід менше 471,9 ден.ед., а половина - більше.
Визначимо медіану і моду графічно. Для того, щоб побудувати моду графічно, на гістограмі потрібно знайти найвищий стовпчик, та поєднати його верхні кути з місцем приєднання до нього сусідніх стовпчиків. Нюанс 1: Якщо найвищий стовпчик стоїть першим або останнім – місцем приєднання неіснуючого стовпчика є нуль. Нюанс 2: Якщо гістограма має 2 сусідніх найвищих стовпчики - побудова виконується збільшеним методом: подвоєнням як модальних стовпчиків, так і сусідніх.
Рис. 1.3. Графічне визначення моди по полігону розподілу домогосподарств за розміром місячного доходу
Рис. 1.4. Графічне визначення медіани за кумулятою грошового доходу
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.84.128 (0.006 с.) |
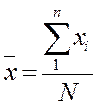 ,
,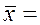 (375 + 390 + 403 + 412 + 437 + 446 + 449 + 454 + 457 + 464 + 467 + 472 + 472 + 483 + 485 + 485 + 488 + 489 + 496 + 504 + 512 + 517 + 526 + 526 + 538) / 25 = 469,88 ден.ед.
(375 + 390 + 403 + 412 + 437 + 446 + 449 + 454 + 457 + 464 + 467 + 472 + 472 + 483 + 485 + 485 + 488 + 489 + 496 + 504 + 512 + 517 + 526 + 526 + 538) / 25 = 469,88 ден.ед.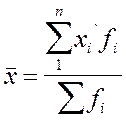 ,
,
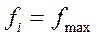 по формулі:
по формулі: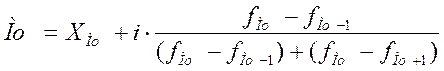 ,
,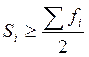 . Конкретне значення медіани в інтервалі обчислюється за формулою:
. Конкретне значення медіани в інтервалі обчислюється за формулою: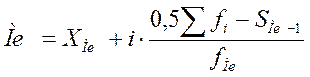 ,
, : 441-474.
: 441-474.