
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механическое движение. Относительность движения. Равномерное и равноускоренное прямолинейное движение.
Вопрос 1. Механическое движение. Относительность движения. Равномерное и равноускоренное прямолинейное движение. Изменение положения тела относительно других тел называется механическим движением. Как видно из определения, в своей основе механическое движение относительно, так изменение положения тела определяется относительно других тел, которые, в свою очередь, могут двигаться относительно третьих и т. д.. Рассмотрим такой пример: стакан стоит на столе движущегося поезда. Очевидно, что стакан неподвижен с точки зрения наблюдателя, едущего в поезде и движется с точки зрения наблюдателя, стоящего на платформе. Основной задачей физики является описание движения тела, т. е. нам надо найти закон, по которому мы могли бы найти положение тела в любой указанный момент времени. Для определения положения тела в физике служит система отсчета. В физике берут какую-то точку (какое-то тело) относительно которого и будем определять положение тела. Такая точка (тело) называется началом отсчета. Также вводят оси координат, имеющие ноль координат в точке начала отсчета. Вообще говоря, наше пространство трехмерное и, следовательно, нам в общем случае надо 3 оси координат, но часто для описания движения такого количества координат не требуется. Для описания движения футболиста по полю достаточно двух координат, а для описания движения автомобиля по шоссе, не имеющем отворотов, достаточно одной координаты. Таким образом к началу отсчета нам надо для определения положения тела добавить направления координатных осей, без чего невозможно построить координатную систему. Помимо этого, к уже построенной системе координат, нам надо для полной характеристики движения достроить систему отсчета времени. Поскольку время имеет единственно возможное направление, то достаточно указать лишь начало отсчета времени. Начало отсчета, направление осей координат и начало отсчета времени определяют систему отсчета. Перемещение – вектор, проведенный из начального положения материальной точки в конечное. Перемещение характеризует изменение радиус-вектора материальной точки. Перемещение показывает, на какое расстояние и в каком направлении смещается тело из начального положения заданное время.
Механическое движение характеризуется средней путевой скоростью, это скалярная величина, равная отношению пути к промежутку времени затраченного на его прохождение. Движение характеризуется мгновенной скоростью — средней скоростью за бесконечно малый интервал времени. Скорость — векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, за которое это перемещение произошло: Вообще говоря скорость при движении зависит от времени, т.е. однако возможно движение, при котором скорость постоянна. Такое движение называется равномерным движением. Рассмотрим перемещение тела при равномерном движении. Для этого рассмотрим проекцию перемещения на одну из осей. Основным свойством равномерного движения является то, что средняя скорость за любой промежуток времени равна мгновенной. Тогда для проекции на ось «x» имеем - уравнение для координаты при равномерном движении. Ниже на рис. приведены графики скорости и координаты от времени при равномерном движении.
Однако в подавляющем числе случаев движения тел не являются равномерными.
Используя тот факт, что путь можно найти, как площадь под графиком Vx(t) видно, что искомая площадь представляет собой трапецию с высотой t, основаниями V и Vo Вопрос 2. Взаимодействие тел. Сила. Законы динамики Ньютона. Для описания движения тела необходима система отсчета. Однако не все системы отсчета одинаковы. По своим свойствам системы отсчета делятся на две группы: инерциальные и неинерциальные. Инерциальная система отсчета - это система отсчета, в которой свободное от внешних воздействий тело движется в ней равномерно и прямолинейно. Однако найти идеальную инерциальную систему отсчета невозможно. Нетрудно сообразить, что для создания такой системы необходимо найти идеально свободное тело, которое можно было бы использовать как начало отсчета, а это невозможно. Первый закон Ньютона утверждает, что существуют инерциальные системы отсчета, в которых тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действия других тел компенсируются. Этот закон является постулатом. Однако, вообще говоря, скорость тела в инерциальной СО изменяется в связи с тем, что на него действуют другие тела. Из данного закона и преобразований Галилея следует, что инерциальных систем отсчета бесконечно много. Действительно, очевидно, что любая система отсчета, начало которой движется с постоянной скоростью относительно инерциальной, сама является инерциальной.
Рассмотрим, для простоты, систему, состоящую из двух тел, одно из которых действует, а другое подвергается действию, и, следовательно, обладает ускорением и меняет свой импульс. Однако опыт показывает, что такое деление на действующее и подверженное действию глубоко ошибочно, поскольку оба тела обладают ускорением и, соответственно, подвергаются влиянию друг друга. Происходит взаимное действие тел друг на друга или взаимодействие тел. Основными законами в физике являются законы сохранения. Поэтому, еще в истоках развития механике пытались найти некоторый инвариант для механического движения, т.е. некоторую величину, которая сохраняется всегда и в любой системе, если только в этой системе нет внешних воздействий. Назовем такую систему замкнутой. Замкнутая система тел - это совокупность тел, взаимодействующих между собой, но не взаимодействующих с другими телами. Для такой системы и пытались найти некоторую постоянную величину, которая исторически получила название количество движения или, более позднее название, импульс. Как и всякий постулат, закон сохранения импульса может быть получен лишь экспериментальным путем. Правда, в данном случае исторически случилось так, что что-то должно сохраняться в замкнутой системе, физики предполагали, но что именно было не понятно. Первым закон сохранения импульса сформулировал Рене Декарт, который предположил, что во вселенной есть известное количество движения, которое не увеличивается и не уменьшается.
Декарт предположил, что поскольку идет разговор о количестве движения, а индикатором движения является скорость, то данная величина (далее будем называть ее по современному импульсом и обозначать как p) пропорциональна скорости: p ~ V и, кроме скорости зависит лишь от свойств самого тела накапливать в себе движение. Эту способность тела Декарт назвал инерционной массой. Тогда, по Декарту, p = mV. Единственно, о чем не догадался Декарт это о том, что импульс, как и скорость, величина векторная и тогда определение импульса будет: а закон сохранения импульса для замкнутой системы (замкнутая система — система тел, для которой равнодействующая внешних сил равна нулю):, где суммирование ведется по всем телам входящим в замкнутую систему, а m i - инерционная масса. В физике действие одного тела на другое называют силой. Рассмотрим какими свойствами она обладает. 1. Сила физическая величина, т.е. это не просто понятие, термин, а физическая величина, которую можно выразить в числах, используя сравнение с некоторым эталоном, принятым за единицу измерения силы. 2. Рассмотрим тело, находящееся в состоянии покоя в инерциальной системе отсчета Подцепим к нему пружину и потянем за нее. Тело сдвинется с места и начнет двигаться в направлении, куда мы его тянем. На наличие силы указывает растяжение пружины. Обратим внимание, что тело двигается именно в ту сторону, куда мы его тянем, что указывает на то, что сила имеет направление, т.е. является векторной величиной. Изменим условия опыта: прицепим другую пружину и будем тянуть за пружины в противоположных направлениях. При этом можно добиться того что тело будет неподвижно, хотя растяжение пружин указывает на наличие сил. Это указывает на то, что силы можно складывать и подтверждает их векторную природу.
Таким образом мы выяснили, что сила это векторная физическая величина. Необходимо связать ее с другими физическими величинами и ввести единицу измерения. Вопрос 3. Импульс тела. Закон сохранения импульса. Проявление закона сохранения импульса в природе и его использование в технике. При движении материальной точки вдоль оси Х действующая на нее F зависит как от координаты тела х. так и от времени. Это означает, сила является функцией от координаты и времени: F = F (х, t). Рассмотрим, как на движение тела влияет длительность действия силы. Для упрощения математических оценок будем считать, что • модуль силы не зависит от координаты х • сила, начиная действовать в момент времени равный 0, остается постоянной в течение всего времени Временной характеристикой действия силы является импульс силы. Импульс силы — произведение силы на длительность ее действия: р=F*t Импульс силы — временная характеристика действия силы. Единица импульса силы - ньютон/c Импульс силы численно равен площади прямоугольника со сторонами F и t Импульс тела — векторная физическая величина, равная произведению массы тела на его скорость и имеющая направление скорости. Единица импульса — килограмм-метр в секунду (кг м/с). Изменение импульса тела определяется импульсом силы, действующей на него; импульс силы характеризуется произведением силы на время ее действия. Следовательно, аналогичное воздействие на тело может очень небольшая сила, действующая значительный промежуток времени, и большая сила, которая действует кратковременно. Этот эффект хорошо известен хоккеистам. Скорость, приобретаемая шайбой при сильном броске, когда время контакта клюшки с шайбой оказывается порядка секунды, примерно совпадает с ее скоростью при мощном, но кратковременном щелчке. Если импульс силы при броске шайбы равен импульсу силы при щелчке, то площади заштрихованных прямоугольников равны.
Замкнутая система — система тел, для которой равнодействующая внешних сил равна нулю. Силы взаимодействия между телами системы называются внутренними силами. При столкновении шаров сила, которая действует на первый шар со стороны второго, по третьему закону Ньютона равна по модулю и противоположна по направлению силе, действующей на второй шар со стороны первого. Запишем выражения для этих сил. В правой части равенства содержится суммарный импульс системы в начальный момент времени, а в левой — сумма импульсов тел в произвольный момент времени, приобретенных в результате взаимодействия (столкновения). Это означает, что при столкновении суммарный импульс системы сохраняется. Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой. Одним из основных примеров проявления закона сохранения импульса является реактивное движение — движение, возникающее при отделении от тела (какой-либо его части) с некоторой скоростью. Например, отделение ядра от ствола оружия. Отдачу испытывают пожарные, направляя водяную струю на горящий объект, Именно благодаря закону сохранения импульса перемещается водный транспорт. В природе встречаются живые организмы, которые перемещаются за счет реактивной отдачи, например медузы. Вопрос 4. Закон всемирного тяготения. Исаак Ньютон выдвинул предположение, что между любыми телами в природе существуют силы взаимного притяжения. Эти силы называют силами гравитации или силами всемирного тяготения. Сила всемирного тяготения проявляется в космосе, Солнечной системе и на Земле. Ньютон обобщил законы движения небесных тел и выяснил, что сила
где Физический смысл гравитационной постоянной вытекает из закона всемирного тяготения. Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах (или если хотя бы масса одного из тел велика). Закон же всемирного тяготения выполняется только для материальных точек и шаров (в этом случае за расстояние принимается расстояние между центрами шаров). Частным видом силы всемирного тяготения является сила притяжения тел к Земле (или к другой планете). Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свободного падения. В соответствии со вторым законом Ньютона
В технике и быту широко используется понятие веса тела. Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете.(Единица веса — ньютон (Н). Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры. Рассмотрим случай, когда тело вместе с опорой не движется. В этом случае сила реакции опоры, а следовательно, и нее тела равен силе тяжести. В случае движения тела вертикально вверх вместе с опорой с ускорением по второму закону Ньютона можно записать В проекции на ось Следовательно, при движении вертикально вверх с ускорением вес тела увеличивается и находится по формуле Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают на себе космонавты как при взлете космической ракеты, так и при торможении корабля при входе в плотные слои атмосферы. Испытывают перегрузки и летчики при выполнении фигур высшего пилотажа, и водители автомобилей при резком торможении. Если тело движется вниз по вертикали, то с помощью аналогичных рассуждений получаем Состояние тела, в котором его вес равен нулю, называют невесомостью. Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением, поэтому в корабле наблюдается состояние невесомости.
Вопрос 5. Масса. Свойства массы. Из твердого вещества можно изготовить однородные тела. Свойство однородности состоит в следующем. Выделим в произвольно взятых точках тела одинаковые по массе части Для однородного тела можно выяснить зависимость массы от его объема. Эта зависимость будет линейной для любых веществ. Однако для разных веществ углы наклона соответствующих графиков к оси объемов различны (рис. 41). Следовательно, можно сделать вывод: отношение массы к объему для данного вещества не зависит от объема, однако для разных веществ эти отношения различны. Например, дни графика 3 (см. рис. 41) это отношение больше, чем для графика 1.
Отношение Среди металлов маленькие плотности имеют калий, магний, литий. Наиболее легкий металл — литий — имеет плотность 534 кг/м3 (это меньше плотности воды). Металл с наибольшей плотностью — осмий. Его плотность 22 570 кг/м3. Плотность вещества связана с его строением. Эта связь проявляется в том, что плотность равна произведению концентрации частиц твердых кристаллических веществ плотность может быть связана с периодом решетки Пусть вещество (например, медь) имеет кубическую гранецентрированную решетку (рис. 42). Тогда в объеме
Если взять массу вещества, равную молярной массе Плотность газов легко изменяется, поэтому в разных изопроцессах она может изменяться. Это становится ясным, если уравнение Менделеева—Клапейрона записать, включив в него плотность. Действительно, 1) при изотермическом процессе (Т = const) плотность газа пропорциональна давлению: 2) при изобарном процессе (р = const) плотность газа обратно пропорциональна температуре: 3) понятно, что при изохорном процессе (V = const) плотность газа не изменяется.
Вопрос 6. Вопрос 7. Вопрос 8. Закон сохранения энергии. Закон сохранения энергии Вопрос 9. Вопрос 10. Вопрос 11. Вопрос 1. Механическое движение. Относительность движения. Равномерное и равноускоренное прямолинейное движение. Изменение положения тела относительно других тел называется механическим движением. Как видно из определения, в своей основе механическое движение относительно, так изменение положения тела определяется относительно других тел, которые, в свою очередь, могут двигаться относительно третьих и т. д.. Рассмотрим такой пример: стакан стоит на столе движущегося поезда. Очевидно, что стакан неподвижен с точки зрения наблюдателя, едущего в поезде и движется с точки зрения наблюдателя, стоящего на платформе. Основной задачей физики является описание движения тела, т. е. нам надо найти закон, по которому мы могли бы найти положение тела в любой указанный момент времени. Для определения положения тела в физике служит система отсчета. В физике берут какую-то точку (какое-то тело) относительно которого и будем определять положение тела. Такая точка (тело) называется началом отсчета. Также вводят оси координат, имеющие ноль координат в точке начала отсчета. Вообще говоря, наше пространство трехмерное и, следовательно, нам в общем случае надо 3 оси координат, но часто для описания движения такого количества координат не требуется. Для описания движения футболиста по полю достаточно двух координат, а для описания движения автомобиля по шоссе, не имеющем отворотов, достаточно одной координаты. Таким образом к началу отсчета нам надо для определения положения тела добавить направления координатных осей, без чего невозможно построить координатную систему. Помимо этого, к уже построенной системе координат, нам надо для полной характеристики движения достроить систему отсчета времени. Поскольку время имеет единственно возможное направление, то достаточно указать лишь начало отсчета времени. Начало отсчета, направление осей координат и начало отсчета времени определяют систему отсчета. Перемещение – вектор, проведенный из начального положения материальной точки в конечное. Перемещение характеризует изменение радиус-вектора материальной точки. Перемещение показывает, на какое расстояние и в каком направлении смещается тело из начального положения заданное время. Механическое движение характеризуется средней путевой скоростью, это скалярная величина, равная отношению пути к промежутку времени затраченного на его прохождение. Движение характеризуется мгновенной скоростью — средней скоростью за бесконечно малый интервал времени. Скорость — векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, за которое это перемещение произошло: Вообще говоря скорость при движении зависит от времени, т.е. однако возможно движение, при котором скорость постоянна. Такое движение называется равномерным движением. Рассмотрим перемещение тела при равномерном движении. Для этого рассмотрим проекцию перемещения на одну из осей. Основным свойством равномерного движения является то, что средняя скорость за любой промежуток времени равна мгновенной. Тогда для проекции на ось «x» имеем - уравнение для координаты при равномерном движении. Ниже на рис. приведены графики скорости и координаты от времени при равномерном движении.
Однако в подавляющем числе случаев движения тел не являются равномерными.
Используя тот факт, что путь можно найти, как площадь под графиком Vx(t) видно, что искомая площадь представляет собой трапецию с высотой t, основаниями V и Vo Вопрос 2. Взаимодействие тел. Сила. Законы динамики Ньютона. Для описания движения тела необходима система отсчета. Однако не все системы отсчета одинаковы. По своим свойствам системы отсчета делятся на две группы: инерциальные и неинерциальные. Инерциальная система отсчета - это система отсчета, в которой свободное от внешних воздействий тело движется в ней равномерно и прямолинейно. Однако найти идеальную инерциальную систему отсчета невозможно. Нетрудно сообразить, что для создания такой системы необходимо найти идеально свободное тело, которое можно было бы использовать как начало отсчета, а это невозможно. Первый закон Ньютона утверждает, что существуют инерциальные системы отсчета, в которых тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действия других тел компенсируются. Этот закон является постулатом. Однако, вообще говоря, скорость тела в инерциальной СО изменяется в связи с тем, что на него действуют другие тела. Из данного закона и преобразований Галилея следует, что инерциальных систем отсчета бесконечно много. Действительно, очевидно, что любая система отсчета, начало которой движется с постоянной скоростью относительно инерциальной, сама является инерциальной. Рассмотрим, для простоты, систему, состоящую из двух тел, одно из которых действует, а другое подвергается действию, и, следовательно, обладает ускорением и меняет свой импульс. Однако опыт показывает, что такое деление на действующее и подверженное действию глубоко ошибочно, поскольку оба тела обладают ускорением и, соответственно, подвергаются влиянию друг друга. Происходит взаимное действие тел друг на друга или взаимодействие тел. Основными законами в физике являются законы сохранения. Поэтому, еще в истоках развития механике пытались найти некоторый инвариант для механического движения, т.е. некоторую величину, которая сохраняется всегда и в любой системе, если только в этой системе нет внешних воздействий. Назовем такую систему замкнутой. Замкнутая система тел - это совокупность тел, взаимодействующих между собой, но не взаимодействующих с другими телами. Для такой системы и пытались найти некоторую постоянную величину, которая исторически получила название количество движения или, более позднее название, импульс. Как и всякий постулат, закон сохранения импульса может быть получен лишь экспериментальным путем. Правда, в данном случае исторически случилось так, что что-то должно сохраняться в замкнутой системе, физики предполагали, но что именно было не понятно. Первым закон сохранения импульса сформулировал Рене Декарт, который предположил, что во вселенной есть известное количество движения, которое не увеличивается и не уменьшается.
Декарт предположил, что поскольку идет разговор о количестве движения, а индикатором движения является скорость, то данная величина (далее будем называть ее по современному импульсом и обозначать как p) пропорциональна скорости: p ~ V и, кроме скорости зависит лишь от свойств самого тела накапливать в себе движение. Эту способность тела Декарт назвал инерционной массой. Тогда, по Декарту, p = mV. Единственно, о чем не догадался Декарт это о том, что импульс, как и скорость, величина векторная и тогда определение импульса будет: а закон сохранения импульса для замкнутой системы (замкнутая система — система тел, для которой равнодействующая внешних сил равна нулю):, где суммирование ведется по всем телам входящим в замкнутую систему, а m i - инерционная масса. В физике действие одного тела на другое называют силой. Рассмотрим какими свойствами она обладает. 1. Сила физическая величина, т.е. это не просто понятие, термин, а физическая величина, которую можно выразить в числах, используя сравнение с некоторым эталоном, принятым за единицу измерения силы. 2. Рассмотрим тело, находящееся в состоянии покоя в инерциальной системе отсчета Подцепим к нему пружину и потянем за нее. Тело сдвинется с места и начнет двигаться в направлении, куда мы его тянем. На наличие силы указывает растяжение пружины. Обратим внимание, что тело двигается именно в ту сторону, куда мы его тянем, что указывает на то, что сила имеет направление, т.е. является векторной величиной. Изменим условия опыта: прицепим другую пружину и будем тянуть за пружины в противоположных направлениях. При этом можно добиться того что тело будет неподвижно, хотя растяжение пружин указывает на наличие сил. Это указывает на то, что силы можно складывать и подтверждает их векторную природу. Таким образом мы выяснили, что сила это векторная физическая величина. Необходимо связать ее с другими физическими величинами и ввести единицу измерения. Вопрос 3. Импульс тела. Закон сохранения импульса. Проявление закона сохранения импульса в природе и его использование в технике. При движении материальной точки вдоль оси Х действующая на нее F зависит как от координаты тела х. так и от времени. Это означает, сила является функцией от координаты и времени: F = F (х, t). Рассмотрим, как на движение тела влияет длительность действия силы. Для упрощения математических оценок будем считать, что • модуль силы не зависит от координаты х • сила, начиная действовать в момент времени равный 0, остается постоянной в течение всего времени Временной характеристикой действия силы является импульс силы. Импульс силы — произведение силы на длительность ее действия: р=F*t Импульс силы — временная характеристика действия силы. Единица импульса силы - ньютон/c Импульс силы численно равен площади прямоугольника со сторонами F и t Импульс тела — векторная физическая величина, равная произведению массы тела на его скорость и имеющая направление скорости. Единица импульса — килограмм-метр в секунду (кг м/с). Изменение импульса тела определяется импульсом силы, действующей на него; импульс силы характеризуется произведением силы на время ее действия. Следовательно, аналогичное воздействие на тело может очень небольшая сила, действующая значительный промежуток времени, и большая сила, которая действует кратковременно. Этот эффект хорошо известен хоккеистам. Скорость, приобретаемая шайбой при сильном броске, когда время контакта клюшки с шайбой оказывается порядка секунды, примерно совпадает с ее скоростью при мощном, но кратковременном щелчке. Если импульс силы при броске шайбы равен импульсу силы при щелчке, то площади заштрихованных прямоугольников равны.
Замкнутая система — система тел, для которой равнодействующая внешних сил равна нулю. Силы взаимодействия между телами системы называются внутренними силами. При столкновении шаров сила, которая действует на первый шар со стороны второго, по третьему закону Ньютона равна по модулю и противоположна по направлению силе, действующей на второй шар со стороны первого. Запишем выражения для этих сил. В правой части равенства содержится суммарный импульс системы в начальный момент времени, а в левой — сумма импульсов тел в произвольный момент времени, приобретенных в результате взаимодействия (столкновения). Это означает, что при столкновении суммарный импульс системы сохраняется. Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой. Одним из основных примеров проявления закона сохранения импульса является реактивное движение — движение, возникающее при отделении от тела (какой-либо его части) с некоторой скоростью. Например, отделение ядра от ствола оружия. Отдачу испытывают пожарные, направляя водяную струю на горящий объект, Именно благодаря закону сохранения импульса перемещается водный транспорт. В природе встречаются живые организмы, которые перемещаются за счет реактивной отдачи, например медузы. Вопрос 4. Закон всемирного тяготения. Исаак Ньютон выдвинул предположение, что между любыми телами в природе существуют силы взаимного притяжения. Эти силы называют силами гравитации или силами всемирного тяготения. Сила всемирного тяготения проявляется в космосе, Солнечной системе и на Земле. Ньютон обобщил законы движения небесных тел и выяснил, что сила
где Физический смысл гравитационной постоянной вытекает из закона всемирного тяготения. Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах (или если хотя бы масса одного из тел велика). Закон же всемирного тяготения выполняется только для материальных точек и шаров (в этом случае за расстояние принимается расстояние между центрами шаров). Частным видом силы всемирного тяготения является сила притяжения тел к Земле (или к другой планете). Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свободного падения. В соответствии со вторым законом Ньютона В технике и быту широко используется понятие веса тела. Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете.(Единица веса — ньютон (Н). Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры. Рассмотрим случай, когда тело вместе с опорой не движется. В этом случае сила реакции опоры, а следовательно, и нее тела равен силе тяжести. В случае движения тела вертикально вверх вместе с опорой с ускорением по второму закону Ньютона можно записать В проекции на ось
| Поделиться:
| |
 равна:
равна: ,
, и
и  - массы взаимодействующих тел,
- массы взаимодействующих тел,  — расстояние между ними,
— расстояние между ними, 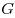 — коэффициент пропорциональности, который называется гравитационной постоянной. Численное значение гравитационной постоянной опытным путем определил Кавендиш, измеряя силу взаимодействия между свинцовыми шарами. В результате закон всемирного тяготения звучит так: между любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки.
— коэффициент пропорциональности, который называется гравитационной постоянной. Численное значение гравитационной постоянной опытным путем определил Кавендиш, измеряя силу взаимодействия между свинцовыми шарами. В результате закон всемирного тяготения звучит так: между любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки. , следовательно,
, следовательно,  . Сила тяжести всегда направлена к центру Земли. В зависимости от высоты
. Сила тяжести всегда направлена к центру Земли. В зависимости от высоты  над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения.
над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. (рис. 7, а).
(рис. 7, а). :
: 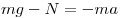 , отсюда
, отсюда  .
. .
. ;
;  ;
;  , т. е. вес при движении по вертикали с ускорением будет меньше силы тяжести (рис. 7, б).
, т. е. вес при движении по вертикали с ускорением будет меньше силы тяжести (рис. 7, б). . Тело однородно, если объемы этих частей
. Тело однородно, если объемы этих частей  одинаковы. Из жидкости и газов также можно «изготовить» тела, заключив их в сосуды.
одинаковы. Из жидкости и газов также можно «изготовить» тела, заключив их в сосуды.
 называется плотностью вещества. Единица плотности — кг/м3.
называется плотностью вещества. Единица плотности — кг/м3. на массу
на массу 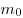 одной частицы (молекулы, атома или иона) вещетва. Действительно,
одной частицы (молекулы, атома или иона) вещетва. Действительно,  , где
, где  - общее число частиц. Итак,
- общее число частиц. Итак, 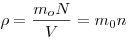 .
. .
.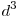 содержится 4 атома. Определим массу и объем этой ячейки.
содержится 4 атома. Определим массу и объем этой ячейки.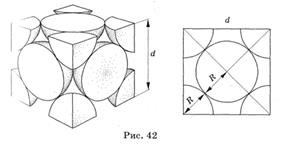
 , то в ней содержится
, то в ней содержится  (число Авогадро) атомов. Следовательно, масса вещества в объеме
(число Авогадро) атомов. Следовательно, масса вещества в объеме  . Таким образом, плотность меди равна
. Таким образом, плотность меди равна  .
. ; следовательно,
; следовательно,  , или
, или  . Отсюда можно сделать следующие выводы:
. Отсюда можно сделать следующие выводы: ;
; ;
;


