
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Саввин Д.Д., Слухаев Н.Г., Семенченко А.И.Содержание книги
Поиск на нашем сайте
ТРЕХФАЗНЫЕ ЦЕПИ
Учебно-методическое пособи е
Новочеркасск ЮРГПУ (НПИ)
УДК 6213.01 (076.5)
Рецензент – канд. техн. наук, доцент В.И. Рожков
Саввин Д.Д., Слухаев Н.Г., Семенченко А.И. Трехфазные цепи: учебно-методическое пособие к индивидуальным заданиям №3, 4 по курсу ″Теоретические основы электротехники" / Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова Новочеркасск ЮРГПУ (НПИ), 2015.– 35 с.
Пособие содержит методические указания к выполнению расчета и оформления задания по трехфазным цепям. Предназначено для студентов энергетических и электротехнических специальностей всех форм обучения, изучающих курс ТОЭ часть II.
УДК 621.307 (076.5)
© Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова, 2015
Расчетное задание № 3 для энергетических специальностей. ТОЭ часть II
РАСЧЕТ ТРЕХФАЗНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ Программа задания О. Нарисовать схему электрической цепи и описать значения ее параметров в комплексной форме. Расчет симметричной трехфазной электрической цепи, включенной на симметричную систему линейных напряжений. 1.1. Составить однофазную схему замещения фазы А. 1.2.Найти комплексы токов и напряжений во всех ветвях однофазной схемы. 1.3. Рассчитать и построить топографическую диаграмму напряжений, совмещенную с векторной диаграммой токов фазы А. 1.4. Используя результаты расчета однофазной схемы замещения, вычислить комплексы токов и напряжений во всех фазах трехфазной цепи. 1.5. Построить топографическую диаграмму напряжений и векторную диаграмму токов симметричной трехфазной цепи, используя диаграмму фазы А. 1.6. Рассчитать потерю и падение напряжения в линии и к.п.д. для системы линия – второй приемник. 2. Параллельно второму приемнику подключить батарею конденсаторов, подобрав ее емкость такой, чтобы коэффициент мощности этого приемника с батареей стал равным 0.98. 3.Вычислить новые значения параметров второго приемника с учетом подключенной батареи конденсаторов. 4.Повторить полностью расчет симметричного режима согласно пунктам программы 1.1-1.5.
5. Расчет несимметричной трехфазной цепи, несимметрия возникла из-за подключения однофазного приемника согласно шифру задания. 5.1. К симметричной цепи подключить однофазный приемник, согласно шифру задания (а, в; в,n и т.д.). 5.2.Составить расчетную систему уравнений по методу контурных токов или методу узловых потенциалов, предварительно обозначив на схеме все токи и напряжения. 5.3. Рассчитать все токи и напряжения и построить топографическую диаграмму напряжений, совмещенную с векторной диаграммой токов. 5.4. Сравнить эту диаграмму с диаграммой симметричного режима и сделать выводы об условиях работы первого и второго приемника после подключения однофазного приемника. 5.5. Выбрать наиболее подходящий способ измерения активной мощности для рассчитываемой трехфазной цепи, нарисовать схему включения ваттметров. Вычислить показания ваттметров. Указания по выбору исходных данных Исходные данные определяются номером варианта, который задается набором из пяти цифр (от 11111 до 99999). В номер варианта входит также одна или две буквы. Первая цифра указывает номер схемы. Рядом со схемой записаны фазные сопротивления цепи в общем виде. Следующие три цифры показывают величины активного сопротивления R и реактивных сопротивлений Пятая цифра указывает номер графы в таблице стандартных линейных напряжений, приведенной ниже. Шестая и седьмая буквы указывают точки подключения однофазного приемника. В номере варианта задаются буквами (a,в; в,n и т.д.) Таблица Нормальный ряд стандартных линейных напряжений трехфазных электрических цепей
Пример расчета трехфазной цепи классическим способом
Исходные данные: схема приведена на рис. 1.1.
Z1 = Z2 = Z3 =21 - j35 – сопротивления первого приёмника, соединённого звездой; Z4 = Z5 = Z6 =6 + j16– сопротивления проводов линии; Z7 = Z8 = Z9 =24 + j24– сопротивления второго приёмника, соединённого звездой.
На схеме обозначены токи во всех ветвях, при этом направление токов в линии и в приёмнике, соединённом звездой, всегда берутся от источника.
Вывод Первый симметричный приёмник подключен на зажимы генератора (А, В, С), следовательно, при подключении однофазного приёмника к зажимам a’b’, который создаёт несимметрию во втором приёмнике, потенциалы А, В, С остались прежними и режим работы первого приёмника останется симметричным. После подключения однофазного приёмника к зажимам a’b’ в режиме работы второго приемника возникнет поперечная несимметрия.
ТОЭ часть II
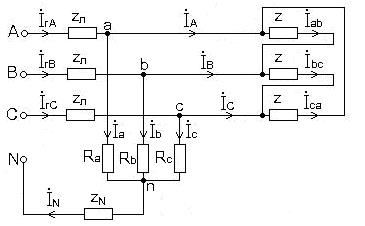
Пример расчета несимметричной трехфазной цепи методом симметричных составляющих 7.1. Схема цепи приведена на рис. 1. 7.1.1. Параметры нагрузок и источника питания 7.1.1.2. Параметры несимметричного приемника. Значения коэффициентов:
Сопротивления нейтрали 7.1.1.3. Сопротивления фаз линии составляющим токам прямой, обратной и нулевой последовательностей:
7.1.1.4. Сопротивления симметричного приемника составляющим токам прямой, обратной и нулевой последовательностей:
Рис. 1
Рис.2
Рис. 3 Рис. 4
Рис. 5 Рис. 6
Рис. 7 Рис. 8
7.1.1.4. Параметры трехфазного источника питания. Значения коэффициента.
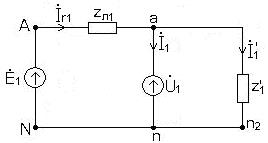
7.2. Расчет токов и напряжений во всех фазах трехфазной цепи. 7.2.1. Разложим заданную систему фазных ЭДС на симметричные составляющие. В данном примере система фазных ЭДСсимметрична и не содержит составляющих обратной и нулевой последовательности. 7.2.2. Преобразуем треугольник в звезду. Схема цепи изображена на рис. 2.
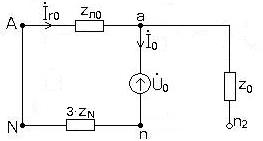
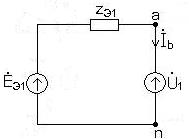
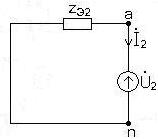
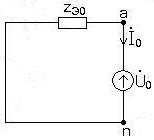
Схемы однофазных цепей для определения симметричных составляющих токов и напряжений прямой, обратной и нулевой последовательности приведены на рис. 3, 4,5. 7.2.3. Уравнения, представляющие фазные напряжения и токи несимметричного приемника через симметричные составляющие.
7.2.4. Расчет параметров преобразованных схем цепей для определения симметричных составляющих токов и напряжений прямой, обратной и нулевой последовательностей.
7.2.5. Схемы преобразованных цепей для определения симметричных составляющих токов и напряжений прямой, обратной и нулевой последовательностей рис. 6, 7, 8. 7.2.6. Система уравнений для определения симметричных составляющих токов и напряжений несимметричного приемника.
Шесть уравнений - шесть неизвестных. Первые три уравнения - основные уравнения. Контурные Кирхгофа для схем цепей рис. 6, 7,8. Дополнительные три уравнения - закон Ома для фаз несимметричного приемника, где соответствующие напряжения и токи разложены на симметричные составляющие по формулам (1). Система уравнений (2) представлена ниже в матричной форме:
Введем обозначения:
Численные значения матриц:
7.2.7. Решение системы уравнений.
7.2.8. Симметричные составляющие токов несимметричного приемника.
7.2.8. 1. Симметричные составляющие напряжений несимметричного приемника.
7.2.9. Определение симметричных составляющих токов симметричного приемника. Схемы рис. 6, 7, 8.
7.2.10. Определение линейных токов симметричного приемника через симметричные составляющие токов симметричного приемника.
7.2.11. Симметричные составляющие фазных напряжений на симметричном приемнике (звезде) рис. 2. Определение через симметричные составляющие токов и соответствующие сопротивления.
7.2.12. Симметричные составляющие напряжений и токов симметричного приемника (треугольник) прямой последовательности.
7.2.13. Симметричные составляющие напряжений и токов симметричного приемника (треугольник) обратной последовательности.
7.2. 14. Фазные напряжения на симметричном приемнике (треугольнике), определенные через симметричные составляющие фазных напряжений.
7.2. 14.1. Фазные токи симметричного приемника (треугольника).
7.2. 14.2. Проверка токов по узловому уравнению Кирхгофа: узлы a, b,c.
7.2. 15. Определение тока нейтрали несимметричного приемника.
7.2. 15.1. Определение смещения нейтрали.
7.2. 16. Определение токов несимметричного приемника через симметричные составляющие токов несимметричного приемника.
7.2. 17. Определение фазных напряжений несимметричного приемника через токи и сопротивления несимметричного приемника по закону Ома.
7.2. 17.1. Определение фазных напряжений несимметричного приемника через симметричные составляющие напряжений. Второй способ.
7.2. 18. Определение симметричных составляющих токов через генератор. Схемы рис. 11, 12, 13. 7.2. 18.1. Первый способ. Используем контурное уравнение Кирхгофа.
7.2. 18.2. Второй способ. Через симметричные составляющие токов приемников. Узловые уравнения Кирхгофа.
7.2. 19. Определение фазных токов (через генератор) через симметричные составляющие токов генератора.
7.2. 19.1. Проверка результатов расчета в цепи по узловому уравнению Кирхгофа для узла N.
7.20. Определение симметричных составляющих напряжений на сопротивлениях линии. Схемы рис. 6,7, 8.
7.20.1. Определение напряжений на сопротивлениях линии через симметричные составляющие.
7.20.2. Проверка результатов расчета напряжений на фазах трехфазной цепи по контурному уравнению Кирхгофа. Вычисление значений фазных ЭДС источника.
Заново определили систему заданных фазных ЭДС. Совпало с исходными данными. 7.3. Вычисление комплексных значений полных мощностей линии, приемников и трехфазного источника двумя способами. Проверка выполнения баланса мощностей. 7.3.1. Определение мощности трехфазного источника двумя способами. 7.3.1.1. Первый способ. Используем формулы для мощности метода симметричных составляющих.
Источник симметричен, отсутствуют ЭДС обратной и нулевой последовательности. 7.3.1.2. Второй способ. Используем формулы для мощности комплексного метода. Через ЭДС и токи генератора.
7.3.2. Определение мощности приемников. 7.3.2. 1. Линия. 7.3.2. 1.1. Первый способ. Используем формулы для мощности метода симметричных составляющих.
7.3.2. 1.2. Второй способ. Используем формулу для активной мощности.
7.3.2. 2. Несимметричный приемник.
7.3.2. 3. Симметричный приемник. 7.3.2. 3.1. Первый способ. Используем формулы для мощности метода симметричных составляющих.
7.3.2. 3.2. Второй способ. Используем формулы для мощности комплексного метода. Через напряжения и фазные токи.
7.3.2. 3.3. Третий способ. Используем формулу для активной мощности.
7.3.2. 4. Мощность, рассеиваемая в нейтрали.
7.3.2. 5. Комплекс полной мощности приемников.
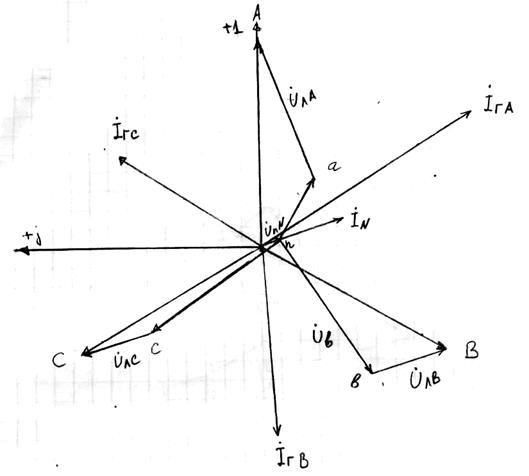
Баланс мощностей выполняется. 7.4. Расчет и построение топографической диаграммы напряжений, совмещенной с векторной диаграммой токов. 7.4.1. Определение потенциалов точек a, b, c для построения топографической диаграммы.
Топографическая диаграмма представлена на рис. 9.
Рис.9
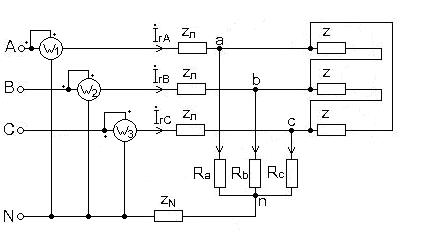
7.5. Выбор схемы измерения активной мощности в несимметричной трехфазной цепи. Вычисление активной мощности. В схеме имеется нейтральный провод, поэтому выбираем схему трех ваттметров, рис. 10.
Совпало с определенной в п. 3.3. активной мощностью.
Рис. 10
Литература 1. Демирчян К.С. и др. Теоретические основы электротехники. 4-е изд. – СПб.: Питер. 2003. – Т.1. 424с. 2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: учеб. для вузов/ 11-е изд., исп. и доп. – М.: Гардарики. 2006. – 701с. 3. Бессонов Л.А. Сборник задач по теоретическим основам электротехники: Учеб. пособие – 4-е изд., перераб. и исп. – М.: Высш. Шк., 2003. – 528с.
Учебно-методическое издание
Трехфазные цепи
Учебно-методическое пособие
Подписано в печать 17.04.2015 Формат 60´84 1/16. Бумага офсетная. Печать цифровая. Усл. печ. л. 1,63. Уч.-изд. л. 1,75. Тираж 100. Заказ № 46-0385.
Южно-Российский государственный политехнический университет Редакционно-издательский отдел ЮРГПУ (НПИ) 346428, г. Новочеркасск, ул. Просвещения, 132
Отпечатано в ИД «Политехник» 346428, г. Новочеркасск, ул. Первомайская, 166
ТРЕХФАЗНЫЕ ЦЕПИ
Учебно-методическое пособи е
Новочеркасск ЮРГПУ (НПИ)
УДК 6213.01 (076.5)
Рецензент – канд. техн. наук, доцент В.И. Рожков
Саввин Д.Д., Слухаев Н.Г., Семенченко А.И. Трехфазные цепи: учебно-методическое пособие к индивидуальным заданиям №3, 4 по курсу ″Теоретические основы электротехники" / Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова Новочеркасск ЮРГПУ (НПИ), 2015.– 35 с.
Пособие содержит методические указания к выполнению расчета и оформления задания по трехфазным цепям. Предназначено для студентов энергетических и электротехнических специальностей всех форм обучения, изучающих курс ТОЭ часть II.
УДК 621.307 (076.5)
© Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова, 2015
Расчетное задание № 3 для энергетических специальностей.
ТОЭ часть II
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.58 (0.012 с.) |



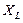 ,
, 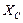 соответственно.
соответственно.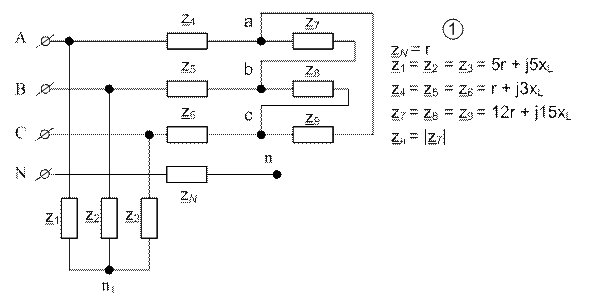
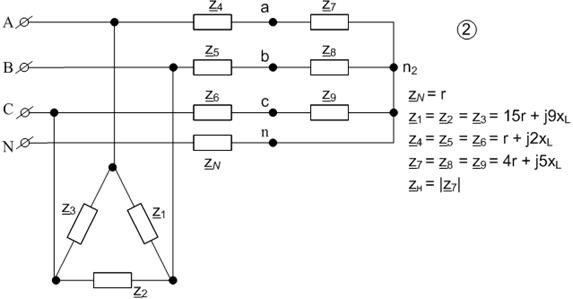
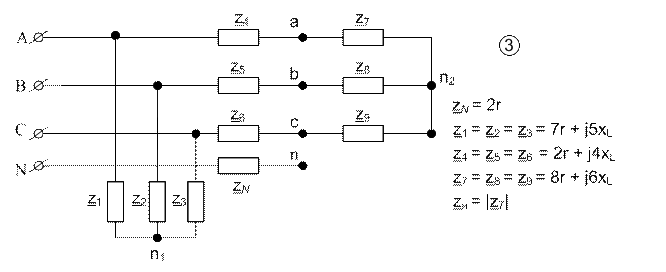

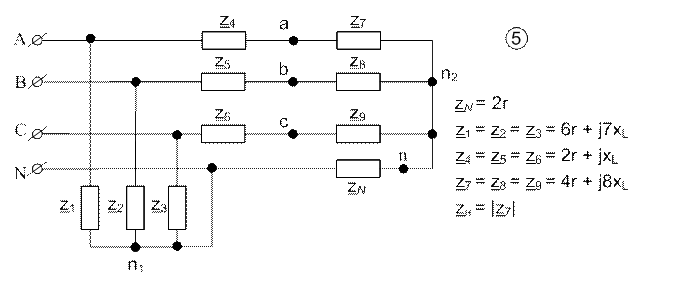
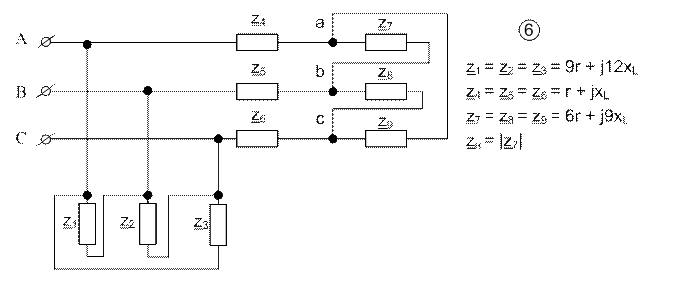

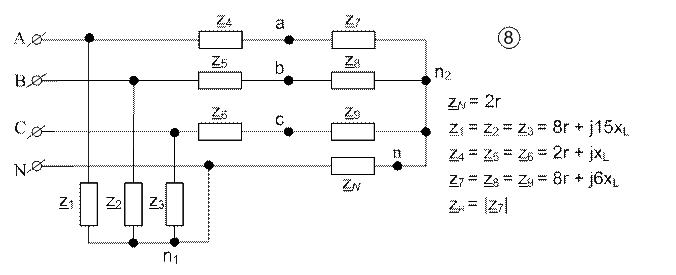
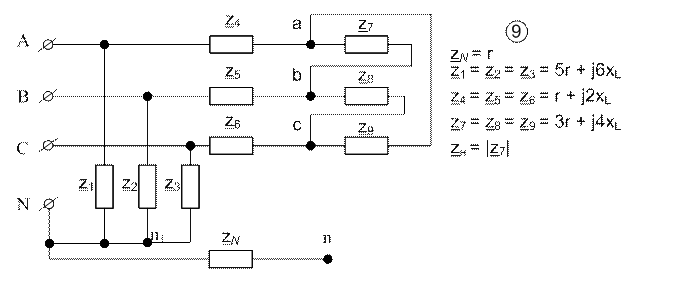
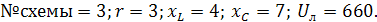
 Рис.1.1. Исходная схема задания.
Рис.1.1. Исходная схема задания.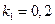 ,
, 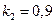 ,
,  .
. ,
, 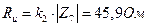 ,
, 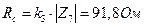 .
.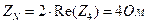 .
.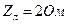 ,
, 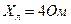 .
.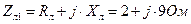 ,
, 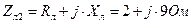 ,
, 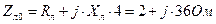 .
.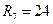 ,
, 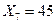 .
.




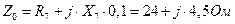
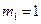 ,
, 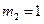 ,
, 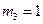 .
. ,
, 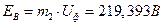 ,
, 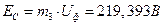 .
.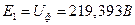 ,
,  ,
, 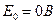 .
.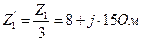 ,
,  ,
,  .
.
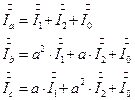 (1)
(1)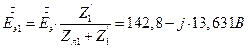
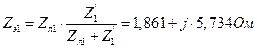


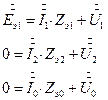
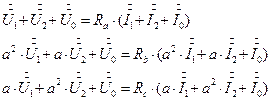 (2)
(2)

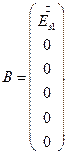
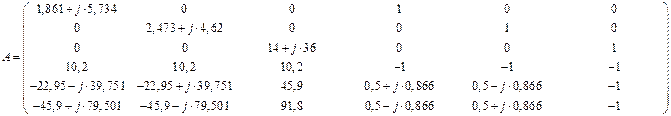
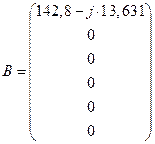
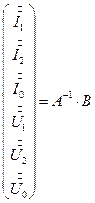

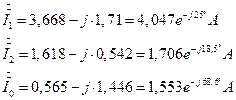
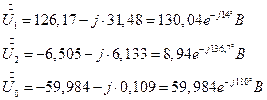

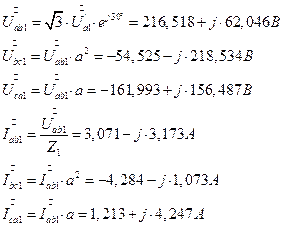
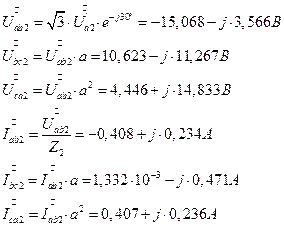

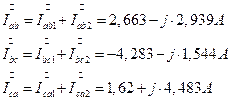

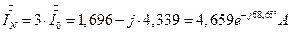

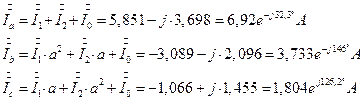

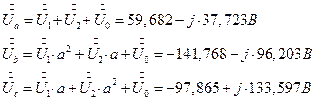


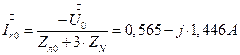
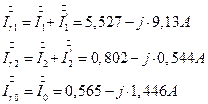
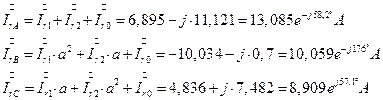
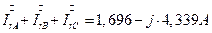
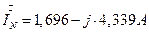

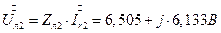

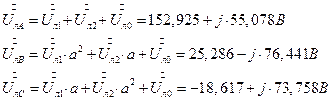
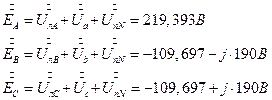
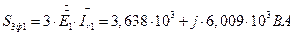
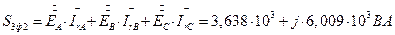
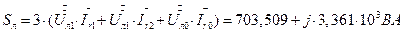

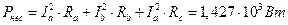





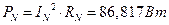


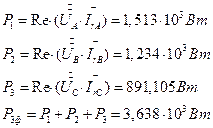
 idp-npi@mail.ru
idp-npi@mail.ru


