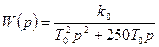Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мета завдання і тривалість роботиЛАБОРАТОРНА РОБОТА № 3. Тема: Ідентифікація об’єкта керування за кривою розгону Мета завдання і тривалість роботи - Набуття навичок визначення динамічних властивостей об’єкта управління за кривою розгону. - 4 год. Короткі теоретичні відомості Динамічні характеристики можуть бути знайдені, якщо на вхід досліджуваного об’єкта подають стандартний сигнал, а реакцію об’єкта фіксують в часі в залежності від виду вхідної дії розрізняють криві розгону, імпульсні і частотні характеристики. Реакція h(t) динамічної системи на ступінчате збурення називають кривою розгону або часовою характеристикою. За зовнішнім виглядом часові характеристики об’єктів можна класифікувати, як характеристики з самовирівнюванням і без самовирівнювання. Типові часові характеристики об’єктів приведені на рис. 3.1. Крива розгону одноманітної ланки із самовирівнюванням – характеристика інерційної (аперіодичної І-го порядку) ланки з параметрами Крива розгону багато ємнісної ланки із самовирівнюванням – характеристика двох послідовно з’єднаних ланок – транспортного запізнення і інерційної ланки. Характеристика одно ємнісного об’єкта без самовирівнювання являється характеристикою інтегруючої ланки, а багато ємнісний об’єкт без самовирівнювання апроксимується характеристикою послідовно включених ланок транспортного запізнення і інтегруючої ланки.
а) б)
ε0=tg α0 ε0=tg α0 в) г) Рисунок 3.1 Типові часові характеристики одно(а і б) і багатоемнісних (в і г) об’єктів з само вимірюванням і без самовимірювання Отримані експериментально криві розгону можна апроксимувати з бажаним степенем точності різними методами: методом площ, метод додатковим членів, методом послідовного логарифмування, методом Ормана і п.п. Існує програма «Артом», в основу якої покладені метод площ Для вводу даних слід про нормувати експериментальні дані за формулою:
де
Для об’єкта із самовирівнюванням нормовані експериментальні дані безпосередньо вводять в ЕОМ, використовуючи програму «Артос». Для об’єкта без самовирівнювання необхідно експериментальними даними здійснити ряд додаткових перетворень. Розглянемо приклад. Приклад. Визначити передавальну функцію барабанного котлоагрегата за каналом «витрати живильної води – рівень води у барабані», яка отримана при збурені витрати живильної води на 5 т/год. Дані експерименту представлені в таблиці 3.1
Таблиця 3.1 – Експериментальні дані
Отже маємо об’єкт безсамовимірювання (астатичний), динамічні властивості якого еквівалентні паралельному з’єднанню інтегруючої ланки і деякої інерційної систем з передавальною функцією
Розрахунки проводяться за алгоритмом: 1. Будуємо експериментальну характеристику, проводимо асимптоту до кривої розгону і визначаємо тангенс кута її нахилу.
2. Будуємо пряму 3. Віднімаємо від прямої
Таблиця 3.2
Використовуємо програму «Аргос». Отримуємо Остаточно передавальна функція об’єкта наступна:
Порядок виконання роботи. 1. Ідентифікувати статичний об’єкт за кривою розгону (таб. 3.1) для цього: - перейти до нормальних величин; - використати програму «Аргос» і визначити передавальну функцію керованого об’єкта з точністю апроксимації ≈ 2,5%; - здійснити висновки. 2. Ідентифікувати астатичні об’єкт керування за кривою розгону (таб.3.2) для цього: - знайти коефіцієнт підсилення інтегруючої ланки; - знайти за допомогою програми «Аргос» передавальну функцію - зробити висновки.
Таблиця 3.2 – Вихідні дані для статичних об’єктів
Таблиця 3.3 – Вихідні дані для астатичних об’єктів
Контрольні запитання 1. Що таке крива розгону? 2. Для яких об’єктів визначають криву розгону? 3. Яку перехідну характеристику мають астатичні об’єкти? 4. Яку перехідну характеристику мають статичні об’єкти? 5. Як визначаються за кривою розгону параметри астатичного об’єкта? Статичного об’єкта? 6. Як визначається нормоване значення збурення?
ЛАБОРАТОРНА РОБОТА № 4. Тема: Ідентифікація об’єкта керування за імпульсними перехідними функціями. Порядок виконання роботи. 1. Згідно вказівки викладача вибрати варіант завдання (таблиця 4.1). 2. Здійснити перехід від імпульсної характеристики до кривої розгону. 3. Перейти до безрозмірних нормованих величин. 4. Використовуючи програму «Аргосх», отримати математичну модель у вигляді передавальної функції. 5. Записати рівняння динаміки отриманої ланки. 6. Здійснити висновки 7. Таблиця 4,1 – Варіанти завдань
4.4 Контрольні запитання 1.Яка існує залежність між частотною функцією w(jw) і імпульсною перехідною функцією h(t)? 2.Яка аналітично представити імпульсну перехідну функцію? 3.Який зв'язок існує між кривою розгону і і імпульсною перехідною функцією? 4.Дати визначення імпульсної характеристики. 5.Динамічні властивості яких об’єктів визначають за допомогою імпульсних характеристик? 6.Яким чином здійснюється побудова кривої розгону на основі імпульсної характеристики?
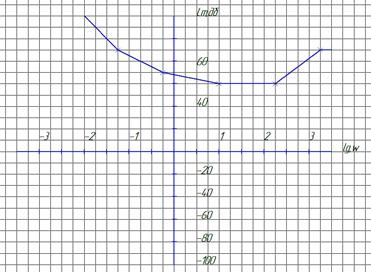
ЛАБОРАТОРНА РОБОТА № 5. Тема: Визначення динамічних характеристик лінійних об’єктів за експериментальними даними – методом частотних характеристик. Порядок виконання роботи. 1Визначити передавальну функцію об’єкта за ЛАЧХ приведеними на рисунку 5.3 – 5.6. 2 Записати рівняння фазочастотної характеристики. 3 Використовуючи MathCad 14.0 побудувати логарифмічні характеристики і порівняти їх з експериментальними характеристиками.
Рисунок 5.3 – ЛАЧХ динамічної ланки.
Рисунок 5.4 – ЛАЧХ динамічної ланки.
Рисунок 5.5 – ЛАЧХ динамічної ланки.
Рисунок 5.6 – ЛАЧХ динамічної ланки.
5.4 Контрольні запитання 1 Як знаходяться спряжені частоти? 2 Як знаходиться коефіцієнт підсилення? 3 Як по вигляду ЛАЧХ визначити чи вміщує передавальна функція об’єкта інтегруючі або диференціюючі ланки? 4 За якою залежністю визначають фазу об’єкта? 5 За якою залежністю визначають амплітуду об’єкта?
ЛАБОРАТОРНА РОБОТА № 6
Тема: Ідентифікація об’єктів методом регресійного аналізу. Порядок виконання роботи. 1 Згідно завдання викладача визначити параметри моделі методом найменших квадратів. Дані експериментів приведені в таб.6.2-6.6 а) апроксимувати об’єкт функцією Таблиця 6.2-Вихідні дані
б) апроксимувати об’єкт функцією Таблиця 6.3-Вихідні дані
в) апроксимувати об’єкт функцією
Таблиця 6.4-Вихідні дані
г) апроксимувати об’єкт функцією
Таблиця 6.5-Вихідні дані
2 Розрахунки провести за допомогою MathCad. 3 Змоделювати на ЕОМ перехідні характеристики. 4 Зробити висновки. 6.4 Контрольні запитання 1. Який експеримент називають пасивним? 2. Який експеримент називають активним? 3. Як визначаються коефіцієнти моделі за експериментальними даними? 4. Як визначається функція похибки?
ЛАБОРАТОРНА РОБОТА № 7
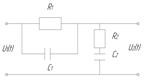
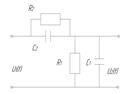
Тема: Моделювання електричних коректуючи пристроїв на ЕОМ Порядок виконання роботи. 1 Згідно завдання викладача знайти математичні моделі активних і пасивних коректуючи пристроїв 2 Симулювати задану схему пасивного коректую чого пристрою за допомогою програми Micro-CAP або Electronic Work Bench 5.x. Елементи для схеми вибирають із верхньої панелі для того, щоб повернути елемент на 90̊ необхідно утримуючи ліву клавішу миші.натиснути необхідну кілкість разів на праву клавішу миші Параметри елементів можна одразу вказувати при виборі елементів із верхньої панелі. Проте можна і пізніше двічі клацнувши на цьому елементі та заповнивши поле VALUE. Щоб отримати графік необхідно встановити точку виходу. Для цього вибираємо компонент TEXT і вписуємо тоді рядок OUT. Тоді переміщуючи цей напис до виходу системи до того моменту поки не отримуємо червону точку. Для активації графіку натискаємо комбінацію клавіш Alt+2. З’являється меню налаштування графіку. У пункті Frequency Range показують необхідний діапазон частот для симуляції електричної схеми. У пункті X Range вказують межі графіку по осі Х. Відповідно у пункті У Range вказують межі графіку по осі у. Спочатку вказується верхня границя, а потім нижня. Третім числом може бути крок сітки графіку. Всі величини вказують через коми в кінці налаштування натискаємо клавішу run. 3 Визначити перехідну характеристику. 4 У середовищі Simulink на основі знайденої передавальної функції змоделювати перехідну характеристику 5 Порівняти результати п.3 і п.4 і зробити висновки.
Таблиця 8.1. Завдання.
Продовження Таблиця 8.1
7.4 Контрольні запитання 1. З якою метою використовують коректуючи ланки? 2 Які бувають коректюючі пристрої? 3 Як визначаються параметри коректуючих пристроїв? 4 Які коректуючи пристрої називаються пасивними,активними? 5 Як отримати перехідну характеристику коректую чого пристрою? 6 Які фізичні закони лежать в основі створення математичної моделі фільтру? 7 Записати залежності, за допомогою яких визначають величину струму через опір,індуктивність і через ємнсть? 8.Які розмірності мають величини що характеризують опір, індуктивність та емність?
ЛАБОРАТОРНА РОБОТА №8
Тема: Дослідження математичних моделей аналітичним способом
Порядок виконання роботи. 1 Для моделі, яка створена в лабораторній роботі № 7, аналітичним способом знайти її розв'язок. 2 Скласти програму обчислення виходу системи для заданої вхідної дії (задається викладачем). 3 Побудувати графік вихідної величини системи при заданій вхідній дії.
8.4 Контрольні запитання 1.Дайте порівняльний аналіз методів, які викори стовуються для розв'язку D - моделей. 2.Дайте визначення прямого і зворотнього пере творення Лапласа. 3.Які властивості прямого перетворення Лапласа використовують для знаходження розв'язку D - моделей? 4.Охарактеризуйте методику знаходження розв'язку D - моделей за допомогою перетворення Лапласа. 5.Яким чином побудувати графік зміни вихідної величини в часі в MatLab?
ЛАБОРАТОРНА РОБОТА № 3. Тема: Ідентифікація об’єкта керування за кривою розгону Мета завдання і тривалість роботи - Набуття навичок визначення динамічних властивостей об’єкта управління за кривою розгону. - 4 год.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.011 с.) |
 і
і  .
.



 , (3.1)
, (3.1)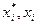 - біжучі значення у безрозмірних і вимірних одиницях;
- біжучі значення у безрозмірних і вимірних одиницях; - значення змінної при
- значення змінної при  і
і  відповідно.
відповідно. . Тобто
. Тобто
 мм/хв.
мм/хв. мм
мм вихідну криву розгону і отримуємо функцію
вихідну криву розгону і отримуємо функцію  . Приводимо функцію
. Приводимо функцію  , мм
, мм




 P, кПа
P, кПа



 Р, МПа
Р, МПа