
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы и алгоритмы балансировки нагрузкиСодержание книги Поиск на нашем сайте
На текущий момент, существует много алгоритмов и методов балансировки нагрузки. Все они используются для достижения следующих целей: · Справедливость – необходимо гарантировать выполнение всех запросов. · Эффективность – все сервера должны использоваться равномерно и брать на себя равномерную нагрузку. · Сокращение времени выполнения запроса – необходимо сократить время между поступлением запроса и его выполнением. · Сокращение времени отклика – необходимо минимизировать время ответа на запрос. · Масштабируемость – при возрастании нагрузки на систему её работа должна оставаться стабильной. Ниже перечислены некоторые из них. Round- Robin – самый простой алгоритм балансировки. Задания назначаются на машины в последовательном порядке, то есть первое задание назначается на первую машину, второе – на вторую машину, и так происходит циклически по кругу. Нагрузка сервера, его вычислительная мощность и время выполнения не являются факторами при выборе сервера. Данный алгоритм лучше всего подходит для систем, в которых производительность всех серверов одинаковая, а требования поставленной задачи к каждому серверу похожи [1]. Weighted Round- Robin – это расширенный round-robin алгоритм, в котором каждому серверу назначается коэффициент веса. Веса назначаются в зависимости от вычислительной мощности машины: чем больше производительность сервера, тем больше коэффициент. Сервера с большим коэффициентом получают большее количество задач. Как и в round-robin алгоритме, задачи назначаются на машины последовательно: на машину назначается количество заданий равное весовому коэффициенту, после чего происходит переход на следующую машину. Это позволяет распределить задания более гибко [1]. Least Connections – алгоритм, который учитывает количество активных подключений к серверам. При поступлении запроса алгоритм выбирает сервер с наименьшим количеством активных подключений и назначает запрос на него [1]. Weighted Least Connections – усовершенствованный Least Connections алгоритм, в котором каждому серверу присваивается весовой коэффициент. Сервер выбирается с наименьшим значением метрики. Метрика вычисляется как количество активных подключений, делённое на весовой коэффициент. Данный алгоритм используется, когда сервера имеют разную производительность. Его целью является равномерное распределение подключений между серверами с большой и низкой производительностью. Чем больше вычислительная мощность сервера, тем большее число подключений он может обработать [1]. Source IP- Hash – данный алгоритм генерирует уникальный хэш-ключ из исходного и целевого IP-адреса клиента. Этот ключ используется для распределения пользователя на определённый сервер. Таким образом, пользователь даже после разрыва соединения будет направлен на тот же сервер, с которым взаимодействовал ранее [2]. Постановка задачи Введём следующие обозначения.
Каждая задача
Необходимо выполнить балансировку так, чтобы нагрузка между всеми машинами была максимально сбалансированной. Иными словами, используя жадный алгоритм, требуется назначить каждую задачу Описание алгоритмов Greedy-Balance Greedy-Balance алгоритм – это простой жадный алгоритм, который в любом порядке перебирает поставленные задачи и назначает каждую из них на машину с минимальной текущей нагрузкой [3]. Пусть даны непустые множества m и n, и пустое множество заданий A. В множестве n элементы располагаются в любом порядке. Из множества задач берётся элемент На Рис. 1.3 приведён псевдокод алгоритма.
Временная сложность алгоритма O (M·N), где M – количество машин, а N – количество задач. При этом, используя очередь с приоритетом, временная сложность алгоритма составит O (log (M) · N). На Рис 1.4 приведён псевдокод алгоритма с использованием очереди с приоритетом.
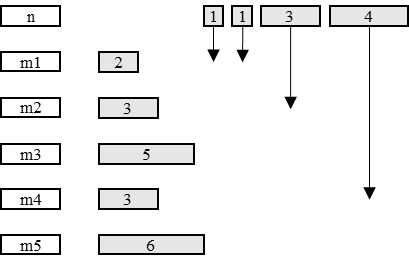
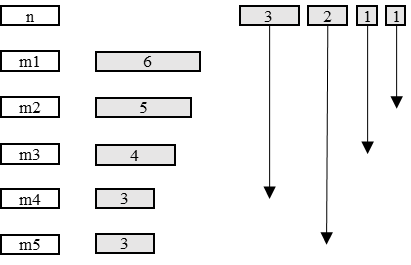
Наглядный пример последовательной работы алгоритма представлен на Рис. 1.5: стрелочки указывают на машину, которой будет назначена текущая задача; каждая задача имеет время выполнения; задачи последовательно назначаются на машину с минимальным временем выполнения на данный момент времени. Период обработки равен 7.
Sorted-Balance Sorted-Balance алгоритм – это разновидность жадного алгоритма, которая в порядке убывания времени выполнения задачи распределяет их на машины с минимальной текущей нагрузкой [3]. Даны непустые множества m и n, и пустое множество заданий A. В начале работы алгоритма все задачи множества n сортируются в порядке убывания по времени выполнения
Временная сложность алгоритма O (
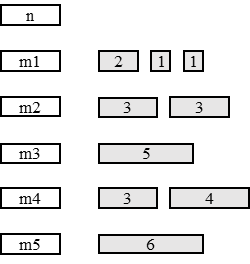
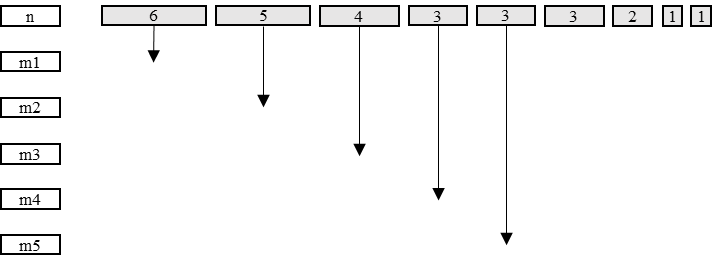
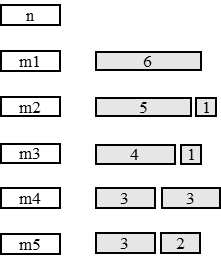
Пример работы алгоритма представлен на Рис. 1.8: в начале работы алгоритма элементы множества n сортируются в порядке убывания, после чего происходит распределение задач между машинами; стрелочки указывают машину назначения. Период обработки равен 6.
Анализ алгоритмов Введём следующие обозначения.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.7.116 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

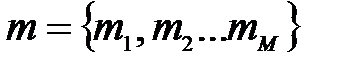 – множество из M машин (серверов);
– множество из M машин (серверов);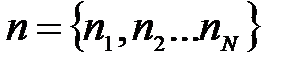 – множество из N задач (запросов);
– множество из N задач (запросов);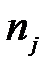 имеет время выполнения
имеет время выполнения 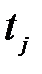 ;
;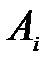 – множество заданий, назначенных на машину
– множество заданий, назначенных на машину 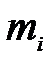 из множества n;
из множества n;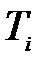 – общее время работы (нагрузка) машины mi.
– общее время работы (нагрузка) машины mi.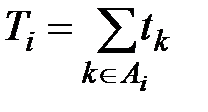
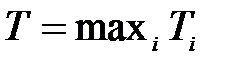 был минимальным.
был минимальным.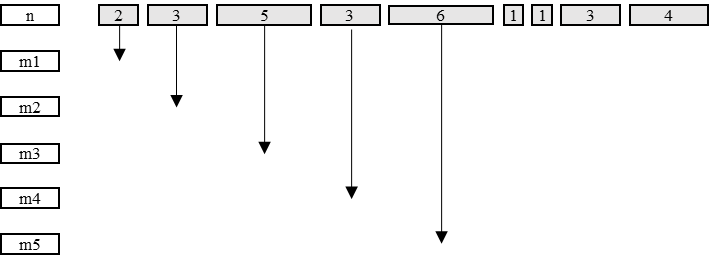
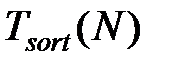 + M·N), где
+ M·N), где 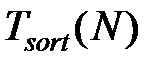 – время выполнения сортировки множества N в порядке убывания времени выполнения. Как и в предыдущем алгоритме, при использовании очереди с приоритетом временная сложность алгоритма составит O (
– время выполнения сортировки множества N в порядке убывания времени выполнения. Как и в предыдущем алгоритме, при использовании очереди с приоритетом временная сложность алгоритма составит O (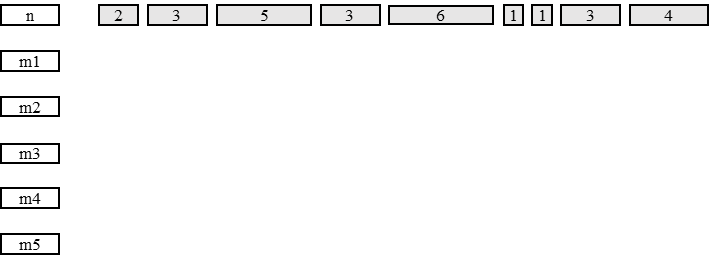
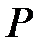 – период обработки текущей балансировки.
– период обработки текущей балансировки.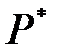 – оптимальная возможная нижняя граница периода обработки текущей балансировки.
– оптимальная возможная нижняя граница периода обработки текущей балансировки.


