
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретические основы рассеивания выбросовСодержание книги
Поиск на нашем сайте
Когда отходящие газы покидают дымовую трубу и поступают в атмосферу, на них начинают воздействовать внешние условия — метеорологические условия (давление, температура, скорость и направление движение воздуха), расположение предприятий и источников выбросов, характер местности, физические и химические свойства выбрасываемых веществ и т. п. (рис. 1). Все эти факторы влияют на распространение дыма от трубы и перенос загрязняющих веществ на дальние расстояния. Горизонтальное перемещение примесей определяется в основном скоростью ветра, а вертикальное — распределением температур в вертикальном направлении. Прогнозирование поведения факела в атмосфере — крайне сложная физико-математическая задача, решение которой затрудняется еще и тем, что в атмосфере процессы нестабильны и могут очень быстро изменяться во времени. В зависимости от атмосферных условий, внешний вид факела может отличаться большим разнообразием. Он может выглядеть как вертикальный столб над трубой, тянуться компактной струей в горизонтальном направлении, быстро размываться в горизонтальном, вертикальном или обоих направлениях и т. д.
Основной эффект рассеивания может достигаться за счет молекулярной и турбулентной диффузии, обеспечивающей одинаковое течение процесса переноса тепла, вредных газов, мелких аэрозолей, водяных паров и т. д. Роль молекулярной диффузии в рассеивании пренебрежительно мала; основную роль играет турбулентная диффузия. Она вызывается двумя группами факторов: динамическими и термическими. Динамические факторы связаны с движение воздушных масс независимо от распределения температур. В нижних слоях атмосферы динамическая диффузия возникает или усиливается за счет макронеровностей рельефа, высокой плотности растительности или искусственных сооружений. Термическая диффузия связана с градиентами температур воздуха по высоте. В большинстве случаев атмосферная диффузия имеет комплексную природу, т. е. турбулентность создается как термическими, так и динамическими факторами. Существует несколько теорий турбулентной диффузии в атмосфере, однако ни одна не дает более или менее точного количественного описания процесса рассеивания. В соответствии с теорией массопереноса, рассеивание, в общем виде, описывается дифференциальным уравнением:
где dС/dt — производная по времени концентрации загрязнителя в точке с координатами x, y, z; ¶ С /¶t0 — градиент по времени концентрации загрязнителя в точке с координатами x = y = z = 0 (это может быть центр устья трубы или точка, учитывающая возвышение факела над устьем, или вообще какая-либо точка, которую в данном случае целесообразно принять за начало координат); u, v, w — скорости распространения загрязнителя вдоль осей x, y, z; ¶ С /¶ х, ¶ С /¶ у, ¶ С /¶ z — градиенты концентраций загрязнителя по отношению к осям координат.
Уравнение составлено в трехмерной системе координат, причем ось х совпадает с направлением основного движения факела, ось у — горизонтальна и перпендикулярна к оси х ось z вертикальна. Положение осей иллюстрируется рис. 2. Толкование уравнения неоднозначно. Некоторые исследователи отождествляют величину и со скоростью ветра и считают, что вектор и совпадает с вектором-скоростью ветра. Другие располагают вектор и по оси факела. И то и другое — частные случаи. В рассматриваемой зоне ветер может дуть не горизонтально, а с наклоном вверх или вниз; ось факела может на довольно значительном участке не совпадать с общим направлением ветра. Ряд трудностей связано определением градиентов концентраций вдоль осей координат. Тем не менее, уравнение (2) позволяет в первом приближении качественно оценить условия выброса и распространения факела. Градиент ¶ С /¶t0 может иметь знак плюс — если на протяжении данного отрезка времени выброс возрастает, знак минус — если выброс уменьшается, или быть равным нулю — при стабильном во времени выбросе. Остальные градиенты всегда имеют знак минус, поскольку по мере удаления от источника выброса концентрация загрязнителя всегда падает. Поскольку градиенты концентрации вдоль осей координат сами по себе непостоянны во времени, необходимо ввести в уравнение вторые производные, после чего оно принимает следующий вид:
Очевидно, что если ¶ С /¶t0 имеет знак плюс, и при этом
то концентрация загрязнителя в данной точке возрастает; при обратном соотношении она снижается. Концентрация остается неизменной, если
или если условия рассеивания в точности компенсируют изменения величины ¶ С /¶t0.Однако последнее крайне маловероятно на практике. Принципиальная разница между правой и левой частью уравнений состоит в том, что абсолютная величина и знак левой части определяются режимом источника выброса и, таким образом, поддаются контролю и управлению. Величина и знак правой части определяются только условиями рассеивания. Решение приведенных здесь первичных уравнений рассеивания связано с очень большими трудностями. Говоря формально, они могут быть решены для условий, существующих в единственный данный момент времени. Но такое решение не имеет никакой практической ценности. Практически приемлемое решение возможно на базе ряда упрощений и усреднений. Рассмотрим влияние некоторых факторов (рис. 1) на процесс рассеивания.
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.109.73 (0.007 с.) |

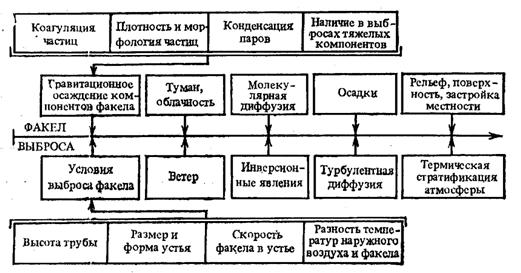 Рис. 1. Схема факторов, влияющих на рассеивание выбросов
Рис. 1. Схема факторов, влияющих на рассеивание выбросов
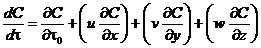 , (1)
, (1)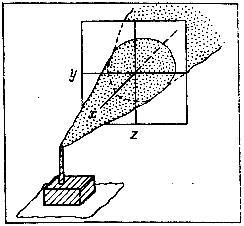 Рис. 2. Факел выбросов в осях координат х – у – z
Рис. 2. Факел выбросов в осях координат х – у – z
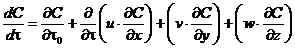 .
.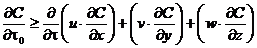 ,
,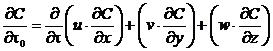 (2)
(2)


