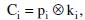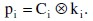Шифры полиалфавитной подстановки

 

Слабая криптостойкость моноалфавитных подстановок преодолевается с применением подстановок многоалфавитных (полиалфавитных). Многоалфавитное шифрование (многоалфавитная замена) заключается в том, что для шифрования последовательных символов исходного текста используются одноалфавитные методы с различными ключами или, иными словами, – свои специальные алфавиты.

Например, первый символ заменяется по методу Цезаря со смещением 18, второй – со смещением 12 и т.д. до конца ключа, задающего переход к новому смещению. Затем процедура продолжается периодически. Более общей является ситуация, когда используется не шифр Цезаря, а последовательность произвольных подстановок, соответствующих одноалфавитным методам.

Шифр Виженера. Самым широко известным и одновременно самым простым алгоритмом такого рода является шифр Виженера (Vigenere). Этот шифр базируется на наборе правил моноалфавитной подстановки, представленных для латинского алфавита из 26 букв шифрами Цезаря со сдвигом от 0 до 25. Каждый из таких шифров можно обозначить ключевой буквой, являющейся буквой шифрованного текста, соответствующей букве a открытого текста. Например, шифр Цезаря, для которого смещение равно 3, обозначается ключевой буквой d. Для полного алфавита русского языка могут использоваться 32 шифра Цезаря со сдвигом от 0 до 32.

Для облегчения понимания и применения этой схемы была предложена матрица, названная “табло Виженера” (рис. 2.21 и 2.22). Все 26 (для русского алфавита – 33, а в данном случае – 32) шифров располагаются по горизонтали, и каждому из шифров соответствует своя ключевая буква, представленная в крайнем столбце слева. Алфавит, соответствующий буквам открытого текста, находится в первой сверху строке таблицы. Процесс шифрования прост – необходимо по букве Х, задаваемой ключом, и букве открытого текста У найти букву шифрованного текста, которая находится на пересечении строки Х и столбца У. В данном случае такой буквой является буква V.

Рис. 2.21. Современное табло Виженера для латинского алфавита

Чтобы зашифровать сообщение, нужен ключ, имеющий ту же длину, что и само сообщение. Обычно ключ представляет собой повторяющееся нужное число раз ключевое слово, чтобы получить строку подходящей длины. Например, если ключевым словом является deceptive / обманчивый /, сообщение «we are discovered save yourself» / мы раскрыты, спасайте себя / шифруется следующим образом.

Расшифровать текст также просто – буква ключа определяет строку, буква шифрованного текста, находящаяся в этой строке, определяет столбец, и в этом столбце в первой строке таблицы будет находиться соответствующая буква открытого текста.

Рис. 2.22. Таблица Виженера для русского алфавита

Рассмотрим еще один пример получения шифротекста с помощью таблицы Виженера. Пусть выбрано ключевое слово АМБРОЗИЯ. Необходимо зашифровать сообщение на русском языке ПРИЛЕТАЮ СЕДЬМОГО.

Выпишем исходное сообщение в строку и запишем под ним ключевое слово с повторением. В третью строку будем выписывать буквы шифротекста, определяемые из таблицы Виженера.

 

 

Преимущество этого шифра заключается в том, что для представления одной и той же буквы открытого текста в шифрованном тексте имеется много различных вариантов – по одному на каждую из неповторяющихся букв ключевого слова. Таким образом, скрывается информация, характеризующая частотность употребления букв. Но и с помощью данного метода все же не удается полностью скрыть влияние структуры открытого текста на структуру шифрованного.

Можно отметить два предложения по усовершенствованию шифра Виженера. Инженером компании AT&T Гилбертом Вернамом (Gilbert Vernam) в 1918 г. было предложено выбирать ключевое слово, по длине равное длине открытого текста, но отличающегося от открытого текста по статистическим показателям (то есть в общем случае речь шла о фрагменте некоторого текста). Кроме того, система Вернама оперирует не буквами, а двоичными числами[4]. Кратко ее можно выразить формулой:

где р_i – i-я двоичная цифра открытого текста; k_i – i-я двоичная цифра ключа; C_i – i-я двоичная цифра шифрованного текста; ⓧ – операция XOR (исключающее “ИЛИ”)[5].

Таким образом, шифрованный текст генерируется путем побитового выполнения операции XOR для открытого текста и ключа. Благодаря свойствам этой операции для расшифровки достаточно выполнить подобную операцию:

Сутью этой технологии является способ выбора ключа. Г.Вернам предложил использовать закольцованную ленту, что означает циклическое повторение ключевого слова, так что его система на самом деле предполагала работу хоть и с очень длинным, но все же повторяющимся ключом. Несмотря на то, что такая схема в силу очень большой длины ключа значительно усложняет задачу криптоанализа, схему, тем не менее, можно взломать, имея в распоряжении достаточно длинный фрагмент шифрованного текста, известные или вероятно известные фрагменты открытого текста либо и то, и другое сразу.

Офицер армейского корпуса связи Джозеф Моборн (Joseph Mauborgne) предложил такие улучшения схемы шифрования Вернама, которые сделали эту схему исключительно надежной. Моборн предложил отказаться от повторений, а случайным образом генерировать ключ, по длине равный длине сообщения. Такая схема, получившая название ленты однократного использования (или схемы с одноразовым блокнотом), взлому не поддается. В результате ее применения на выходе получается случайная последовательность, не имеющая статистической взаимосвязи с открытом текстом. Поскольку в этом случае шифрованный текст не дает никакой информации об открытом тексте, нет способа и взломать код.

Сложность практического применения этого метода заключается в том, что и отправитель, и получатель должны располагать одним и тем же случайным ключом и иметь возможность защитить его от посторонних. Поэтому, несмотря на все преимущества шифра Вернама-Моборна перед другими шифрами, на практике к нему прибегают редко.

 

Шифр “двойной квадрат” Уитстона. В 1854 г. англичанин Чарльз Уитстон разработал новый метод шифрования биграммами, который называют “двойным квадратом”. Свое название этот шифр получил по аналогии с полибианским квадратом, изобретенным в древнем мире. Шифр Уитстона открыл новый этап в истории развития криптографии. В отличие от полибианского шифр «двойной квадрат» использует сразу две таблицы, размещенные по одной горизонтали, а шифрование идет биграммами, как в шифре Плейфейера. Эти не столь сложные модификации привели к появлению на свет качественно новой криптографической системы ручного шифрования. Шифр «двойной квадрат» оказался очень надежным и удобным и применялся Германией даже в годы Второй мировой войны.

Поясним процедуру шифрования этим шифром на примере. Пусть имеются две таблицы со случайно расположенными в них буквами русского алфавита (рис. 2.23)[6]. Перед шифрованием исходное сообщение разбивают на биграммы. Каждая биграмма шифруется отдельно. Первую букву биграммы находят в левой таблице, а вторую букву – в правой таблице. Затем мысленно строят прямоугольник так, чтобы буквы биграммы лежали в его противоположных вершинах. Другие две вершины этого прямоугольника дают буквы биграммы шифротекста. Первый символ шифрованной пары должен лежать в одной строке с первым символом исходной.

Ж

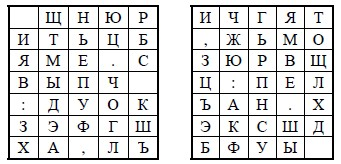
Рис. 2.23. Две таблицы со случайно расположенными символами русского алфавита для шифра «двойной квадрат»

 

Предположим, что шифруется биграмма исходного текста ИЛ. Буква И находится в столбце 1 и строке 2 левой таблицы. Буква Л находится в столбце 5 и строке 4 правой таблицы. Это означает, что прямоугольник образован строками 2 и 4, а также столбцами 1 левой таблицы и 5 правой таблицы. Следовательно, в биграмму шифротекста входят буква О, расположенная в столбце 5 и строке 2 правой таблицы, и буква В, расположенная в столбце 1 и строке 4 левой таблицы, т.е. получаем биграмму шифротекста ОВ.

Если обе буквы биграммы сообщения лежат в одной строке, то и буквы шифротекста берут из этой же строки. Пусть первый символ имеет позицию (s, c) в левой таблице. Тогда он заменяется тем символом правой таблицы, какой там стоит на позиции (s, c). Пусть второй символ имеет позицию (s2, c2) в правой таблице. Тогда он заменяется тем символом левой таблицы, какой там стоит на позиции (s2, c2).

Поэтому биграмма сообщения ТО превращается в биграмму шифротекста ЖБ. Аналогичным образом шифруются все биграммы сообщения:

ЖБ

Шифрование методом «двойного квадрата» дает весьма устойчивый к вскрытию и простой в применении шифр. Взламывание шифротекста «двойного квадрата» требует больших усилий, при этом длина сообщения должна быть не менее тридцати строк.

Расшифровывание требует тех же действий, что и шифрование, только в обратном порядке. Обратный порядок означает, между прочим, что первая буква биграммы шифротекста выбирается в правой таблице, а вторая – в левой.

Две таблицы со случайно расположенными в них буквами естественного алфавита можно рассматривать как два секретных ключа. В то же время их можно рассматривать как форму представления двух специальных алфавитов для записи шифротекстов. Это доказывает, что шифр “двойной квадрат” Уитстона является частным случаем много алфавитных шифров.

Применение перестановок

Все рассмотренные выше методы основывались на замещении по определенным правилам символов открытого текста на естественном языке различными символами специального алфавита (алфавитов), предназначенных для записи шифрованного текста. Принципиально иной класс преобразований строится на использовании перестановок букв открытого текста. Шифры, созданные с помощью перестановок, называют перестановочными шифрами.

Шифр «Лесенка». Простейший из перестановочных шифров использует преобразование “лесенки”, заключающееся в том, что открытый текст записывается вдоль наклонных строк определенной длины («ступенек»), а затем считывается построчно по горизонтали. Например, чтобы шифровать сообщение «meet me after the toga party» /встретьте меня после вечеринки в тогах/ по методу лесенки со ступеньками длиной 2 символа, запишем это сообщение в виде:

Шифрованное сообщение будет иметь следующий вид:

MEMATRHTGPRYETEFETEOAAT

Количество ступенек в «лесенке» рассматривается как ключ шифра. Такой шифр особой сложности для криптоанализа не представляет. Дешифровка может быть осуществлена на основе перебора вариантов количества ступенек в «лесенке».

При расшифровке необходимо определить количество символов в зашифрованной строке и разделить шифрованный текст на равные части в соответствии со значением ключа (количества ступенек в «лесенке»). Первая часть образует первую строку лесенки, вторая часть – вторую и т.д. Дальнейшая расшифровка не представляет труда. При делении с остатком необходимо иметь в виду, что последняя «лесенка» будет «не достроена» за счет нижних ступенек, что характерно для приведенного простого примера.

Шифр вертикальной перестановки. Более сложная схема предполагает запись текста сообщения в горизонтальные строки одинаковой длины и последующее считывание текста столбец за столбцом, но не по порядку, а в соответствии с некоторой перестановкой столбцов. Порядок считывания столбцов при этом становится ключом алгоритма. Рассмотрим пример шифрования следующей фразы: attack postponed until two am /атака отложена до двух ночи/. Первоначально фраза записывается построчно с помощью матрицы размером 4×7, затем с использованием ключа преобразуется в шифротекст:

Буквы x, y, z используются в данном случае как буквы-заполнители.

Простой перестановочный шрифт очень легко распознать, так как буквы в нем встречаются с той же частотой, что и в открытом тексте. Например, для только что рассмотренного способа шифрования с перестановкой столбцов анализ шифра выполнить достаточно просто – необходимо записать шифрованный текст в виде матрицы и перебрать возможные варианты перестановок для столбцов. Можно использовать также таблицы значений частоты биграмм и триграмм.

Перестановочный шифр можно сделать существенно более защищенным, выполнив шифрование с использованием перестановок несколько раз. Оказывается, что в этом случае примененную для шифрования перестановку воссоздать уже не так просто. Например, если предыдущее сообщение шифровать еще раз с помощью того же самого алгоритма, то результат будет следующим:

Чтобы нагляднее представить то, что мы получим в итоге повторного применения перестановки, сопоставим каждую букву исходного открытого текста с номером соответствующей ей позиции. Наше сообщение состоит из 28 букв, и исходной последовательностью будет последовательность:

После первой перестановки получим последовательность, которая все еще сохраняет некоторую регулярность структуры.

После второй перестановки получается следующая последовательность.

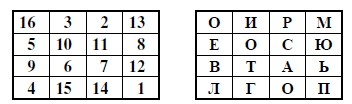
Регулярность этой последовательности уже совсем не просматривается, поэтому ее криптоанализ потребует значительно больше усилий.

Если известен ключ, расшифровка весьма проста и не требует пояснений.

Применение магических квадратов. В средние века для шифрования перестановкой применялись и магические квадраты. Магическими квадратами называют квадратные таблицы с вписанными в их клетки последовательными натуральными числами, начиная от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.

Шифруемый текст вписывали в магические квадраты в соответствии с нумерацией их клеток (первая буква записывалась в клетку под номером 1, вторая – в клетку под номером 2 и т.д.). Если затем выписать содержимое такой таблицы по строкам, то получится шифротекст, сформированный благодаря перестановке букв исходного сообщения. В те времена считалось, что созданные с помощью магических квадратов шифротексты охраняет не только ключ, но и магическая сила.

Пример магического квадрата и его заполнения сообщением ПРИЛЕТАЮ ВОСЬМОГО показан на рис. 2.24.

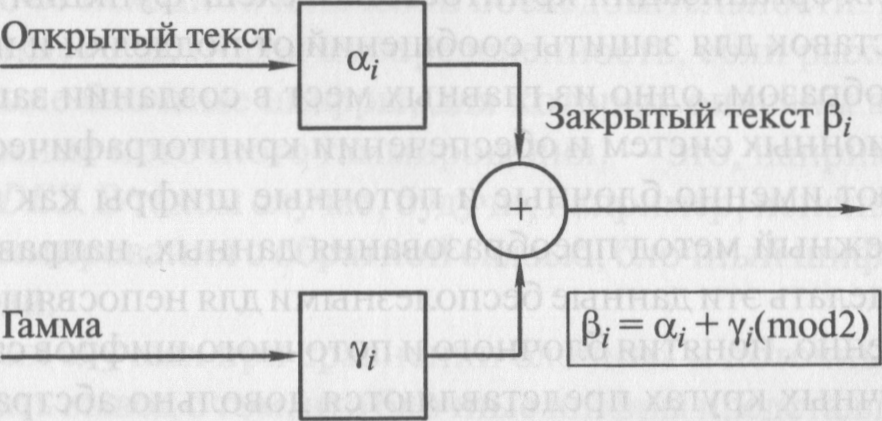
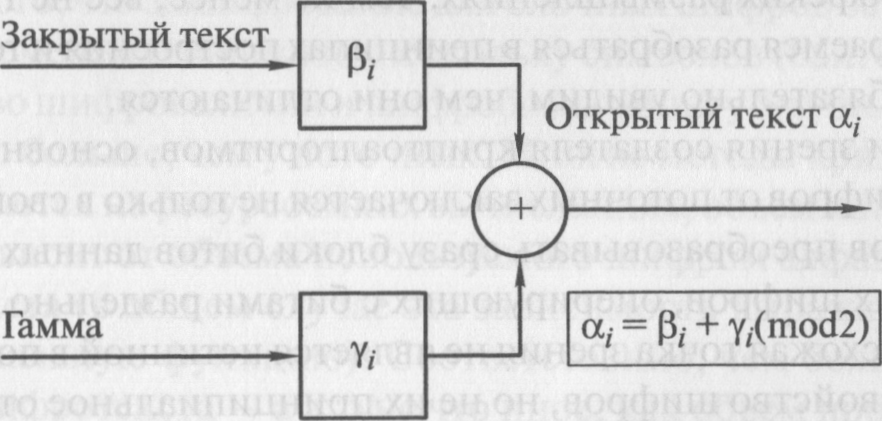
Рис. 2.24. Пример магического квадрата 4x4 и его заполнения сообщением ПРИЛЕТАЮ ВОСЬМОГО

Шифротекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вполне загадочный вид:

ОИРМ ЕОСЮ ВТАЬ ЛГОП

Число магических квадратов быстро возрастает с увеличением размера квадрата. Существует только один магический квадрат размером 3x3 (если не учитывать его повороты). Количество возможных магических квадратов 4x4 составляет уже 880, а количество магических квадратов 5x5 – около 250 000. В связи с этим магические квадраты средних и больших размеров могли служить хорошей базой для обеспечения нужд шифрования того времени, поскольку практически нереально выполнить вручную перебор всех вариантов для такого шифра в целях его дешифровки.

Что касается расшифровки, то она при наличии ключа (то есть магического квадрата) чрезвычайно проста.

Метод  гаммирования

Современный метод гаммирования базируется на методе одноразового блокнота Джозефа Моборна, который нами уже рассматривался. В годы Второй мировой войны этот метод был действительно труднореализуем, однако в условиях применения современных информационных технологий метод гаммирования стал одним из самых распространенных. Данный метод относится к категории методов замены (подстановки), но обычно его рассматривают отдельно.

Процесс шифрования заключается в данном случае в генерации гаммы шифра и наложении этой гаммы на исходный открытый текст. Наиболее часто на практике применяется двоичное гаммирование. В этом случае символы текста и гаммы представляются в двоичных кодах, а затем каждая пара двоичных разрядов складывается по модулю 2[7]. При необходимости двоичные коды можно преобразовать в обычный текст.

Процедура гаммирования на передаче и приеме представлена на рис. 2.25. При расшифровывании операция проводится повторно, в результате получается открытый текст. Символы текста и гаммы здесь также представляются первоначально в двоичных кодах.

Соответствие между буквенно-цифровыми символами и их двоичными кодами регулируется различными стандартами. В таблице 2.10 представлены коды буквенных символов русского языка в стандарте Windows 1251 и их двоичное представление. Этот стандарт представляет собой расширение стандарта ASCII для символов русского языка. В таблице 2.11 представлено кодирование латинских букв и некоторых других символов в ASCII.

Передатчик

 

Приемник

 

 

Рис.2.25. Процедура шифрования, основанная на «наложении» гамма-последовательности на открытый текст

 

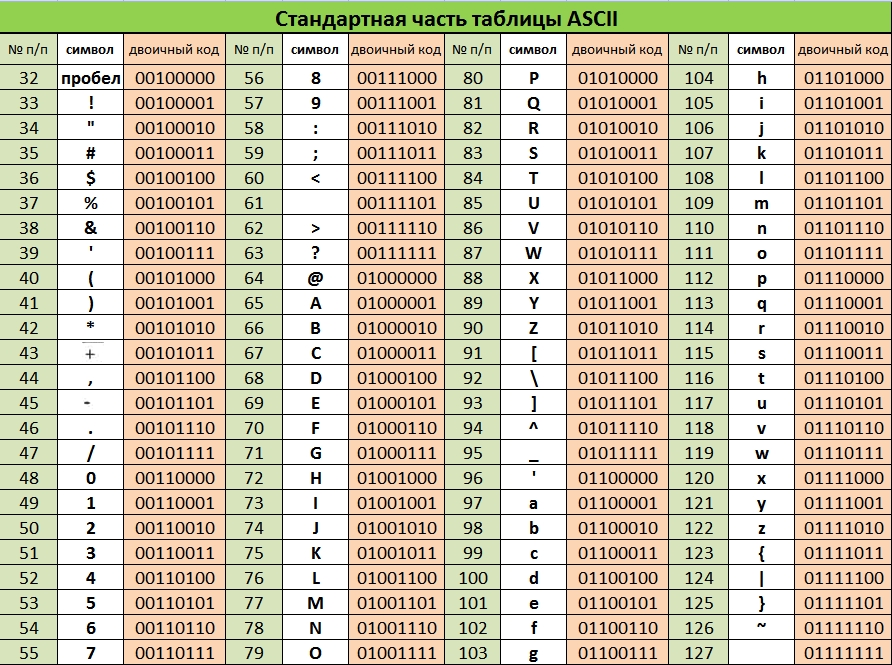
Символы 0 – 31 ASCII (двоичные коды от 00000000 до 00011111) выполняют управляющие функции и не отображаются графическими знаками. В результате гаммирования может быть получен двоичный код, соответствующий этим символам. В этом случае при необходимости исключить в передаваемом сообщении двоичное отображение данных, восемь двоичных разрядов можно представить как две шестнадцатеричные цифры. Для общности с помощью двух шестнадцатеричных цифр можно отображать любой символ, соответствующий ASCII и Windows 1251. Соответствие между шестнадцатеричными и двоичными числами показано в табл. 2.12.

Приведем упрощенный пример шифрования / расшифровывания методом двоичного гаммирования. Необходимо зашифровать, а затем расшифровать короткую строку на русском языке РОССИЯ – 2018. В соответствии с таблицами 2.10 и 2.11 двоичное представление этой строки будет следующее:

 

1101 0000 1100 1110 1101 0001 1101 0001 1100 1000 1101 1111 0010 1101

0011 0010 0011 0000 0011 0001 0011 1000

 

С учетом таблицы 2.12 покажем шестнадцатеричное представление данного текста (два шестнадцатеричных символа соответствуют восьми бинарным):

 

D0 CE D1 D1 C8 DF 2D 32 30 31 38

 

В качестве случайно определенной гаммы, представляющей собой ключ для кодирования, принимается следующая строка, представленная в шестнадцатеричном виде:

 

05 0C 17 7F 0E 4E 37 D2 94 10 09

 

В двоичном виде эта гамма может быть представлена следующим образом:

 

0000 0101 0000 1100 0001 0111 0111 1111 0000 1110 0100 1110 0011 0111

1101 0010 1001 0100 0001 0000 0000 1001

Проводим двоичное гаммирование:

 

Исх. биты	1101	0000	1100	1110	1101	0001	1101	0001
Гамма	0000	0101	0000	1100	0001	0111	1111	0000
Результат	1101	0101	1100	0010	1100	0110	0010	0001

 

Исх. биты	1100	1000	1101	1111	0010	1101	0011	0010
Гамма	0000	1110	0100	1110	0011	0111	1101	0010
Результат	1100	0110	1001	0001	0001	1010	1110	0000

 

Исх. биты	0011	0000	0011	0001	0011	1000
Гамма	1001	0100	0001	0000	0000	1001
Результат	1010	0100	0010	0001	0011	0001

 

В шестнадцатеричном виде зашифрованный текст будет выглядеть следующим образом:

D5 C2 C6 21 C6 91 1A E0 A4 21 31

 

 

 

Таблица 2.10.

Коды букв русского языка Windows 1251 и

их двоичное представление

 

 

 

 

 

Таблица 2.11

 

Коды  латинских букв, цифр и некоторых других символов в ASCII и

их двоичное представление

 

 

 

Таблица 2.12