Основные кинематические зависимости механизма.

Угол поворота креста – ψ зависит от числа его пазов – z:

Ψ = 2π / z = 360^o                                  (6.26)

Из треугольника О₁ А О₂ следуют соотношения основных размеров механизма:

                     R₁²  + R₂² = ℓ² ;

                     R₁ = ℓ · sin (ψ/2) = ℓ · sin (π/z).            (6.27)

Длину паза креста – h можно определить при расположении оси водила и оси паза на межцентровой линии О₁О₂ из соотношения:

                 h = R₁ + r_p + Δ + R₂ - ℓ,

где r_p – радиус ролика;

Δ – зазор между поверхностью ролика и основанием паза кре- ста.

Поскольку водило вращается с постоянной угловой скоростью – ω₁ постольку время поворота и выстоя креста попорционально углам поворота водила φ_р и φ_х :

время поворота креста t_p = 30 · φ_р / (π·n);

время выстоя креста t_х = 30 · φ_х / (π·n).

Таким образом, коэффициент срабатывания креста пропорционален углам поворота:

                     K = t_x / t_p = φ_x / φ_p

Из треугольника О₁АО₂ также следует, что φ_p / 2 = π / 2 – ψ / 2.

Имея в виду, что ψ = 2π / z, получим φ_p = π (z – 2)/z. (6.28)

Поскольку φ_x = 2π - φ_p , получим φ_х = π (z + 2)/z.         (6.28)

Пользуясь этими значениями φ_p и φ_x, выразим значение коэффициента срабатывания – К через число пазов – z:

            K = t_x / t_p = φ_x / φ_p = z + 2 / (z – 2).                (6.29)

Анализируя формулу (6.29), можно сделать следующие выводы:

1. число пазов креста – z не может быть менее трех;

2. максимальное значение – К_max = 5 при числе пазов z = 3.

Кинематический цикл – Т_к  механизма равен времени одного оборота водила, т.е.

                                   Т_к = 60 / n, c

С другой стороны кинематический цикл равен сумме времени рабочего и холостого ходов:

                          T_k = t_p + t_x.

 

Из формулы (6.29) следует, что t_х = K · t_р. Следовательно

Т_k = t_p + K · t_p.

Отсюда следует, что

t_p = T_k · 1 / (K + 1) и t_x = T_k · K / (K + 1)       (6.30)                                                                               

Аналогичным образом, учитывая, что φ_p + φ_x = 2π  и φ_х = K · φ_p, получим:

φ_р = 2π · 1 / (К + 1); φ_х = 2π · К / (К + 1) (в радианах) (6.31)

или

φ_р = 360 · 1 / (К + 1); φ_х = 360 · К / (К + 1) (в градусах)

 

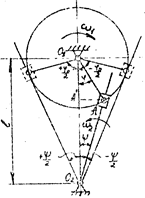
Из формулы (6.30) следует, что при одном и том же кинематическом цикле Т_к время выстоя креста будет зависеть от числа пазов.

Следовательно, чем меньше пазов имеет крест, тем больше у него доля выстоя в кинематическом цикле. Поскольку в автоматах технологические операции производятся во время выстоя транспортирующего органа, постольку кресты с малым числом пазов более выгодны. Однако ныне мы увидим, что с точки зрения динамики кресты с малым числом пазов менее выгодны.

В период движения механизм мальтийского креста представляет собой кулисный механизм (рис.21). При одинаковом отношении межцентрового расстояния ℓ к радиусу кривошипа (водила) R₁

 

λ = ℓ / R₁

 

механизма мальтийского креста и кулисного механизма соотношения углов поворота, скоростей и ускорений их звеньев в точности совпадают.

 

 

 

Рис.21. Схема работы мальтийского креста в интервале рабочего хода.

 

    Поэтому также, как и для кулисного механизма, отсчитывая угол поворота водила φ от межцентровой линии О₁О₂ в пределах значений от 0 до ± φ_р / 2 по формуле (6.21), можно определить соответствующие значения углов поворота креста - ψ в пределах от 0 до ± ψ / 2.

Для тех же значений углов поворота водила можно определить соответствующие значения угловой скорости креста - ω₂, рад/с по формуле (6.22) и углового ускорения креста - ε₂, рад/с² по формуле (6.25).

    При пользовании формулами следует учитывать, что в первой половине поворота углы φ, отсчитываемые от среднего положения, считаются отрицательными, во второй – положительными.

    Угловая скорость креста весь период движения положительна. Она достигает максимального значения в среднем положении креста (φ = 0) и может быть найдена по формуле (6.23). Угловое ускорение креста ε₂ положительно в первую половину движения (– φ_р / 2  < φ < 0) и отрицательно во второю половину движения при (0 < φ < φ_р / 2).

    Максимальное угловое ускорение будет при отклонении водила на угол θ от линии центров О₁О₂. Для определения угла θ производную уравнения (6.25) следует приравнять нулю. После преобразования получаем                 

                           __________          

           соs θ = (√λ⁴ + 34λ² +1 – (λ² + 1)) /(4λ).                  (6.32)

 

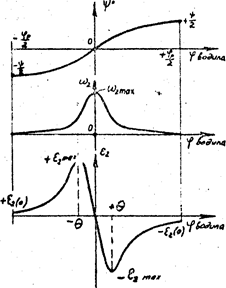
    Максимальные значения угловых ускорений ε₂ и угла θ для наиболее распространенных крестов приведены в таблицы ХХ – 5 учебника [I]. Из этой таблицы видно, что чем меньше пазов у креста, тем больше его угловое ускорение. Например, угловое ускорение креста почти в 30 раз больше ускорения креста с 6 пазами:

    Таким образом, кресты с большим числом пазов, с точки зрения динамики работы механизма, применять выгоднее.

     На рис.22 показаны графики углов поворота – ψ, угловой скорости – ω₂ и углового ускорения – ε₂ креста в зависимости от угла поворота водила – φ, построенные по уравнениям (6.21), (6.22) и (6.25).

 

 

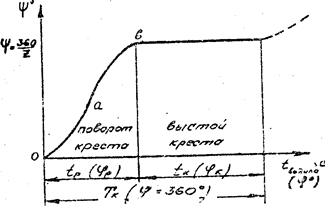
Рис.22. Угол поворота, скорость и ускорение креста.

Из графика ускорения видно, что в начальный и конечный моменты поворота креста, когда ролик входит в паз и выходит из него, ускорение креста не равно нулю, а имеет некоторое начальное ускорение – ε₂₍₀₎ , что приводит к возникновению толчков под действием мгновенно приложенной силы инерции. Можно легко доказать, что:

            ε₂₍₀₎ = ω₁² · tg (π/2)                                        (6.33)

Отсюда следует, что чем меньше число пазов – z, тем больше величина нежелательного начального ускорения.

На рис.23 показана синхрограмма работы мальтийского креста. Угол поворота креста – ψ определяется по формуле (6.26), кинематический цикл – Т_к  по формуле (2.1), продолжительность поворота – t_p  и время выстоя -  t_x  по формулам (6.31), коэффициент срабатывания – К по формуле (6.29). Участок графика оав поворота креста строится по формуле (6.21).

 

 

Рис.23. Синхрограмма механизма мальтийского креста.

 

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ ПО ТЕМЕ

 

1. Базисные механизмы машин-автоматов, определение и примеры.

2. Общие кинематические зависимости базисных механизмов.

3. Кривошипно-ползунный механизм, схема, законы движения ползуна, синхрограмма.

4. Кулисный механизм, схема, законы движения кулисы, синхрограмма.

5. Четырехзвенный механизм, схема, теорема Грасгофа, синхрограмма.

6. Механизм мальтийского креста, схема, законы движения креста, синхрограмма.

7. Кулачковые механизмы, схемы, основные законы движения центра ролика.

 

ТЕСТЫ ПО ТЕМЕ

 

17. Чем образован базисный механизм?

17.1. Ведущим и ведомым звеном

17.2. Первой и второй структурными группами механизма

17.3. Ведущим звеном и первой структурной группой

17.4. Ведомым звеном и второй структурной группой

 

18. В чем отличие аксиального и дезаксиального кривошипно-ползунного механизмов?

18.1. Центр вращения кривошипа лежит на оси движения ползуна.

18.2. Оси ползуна и шатуна совпадают

18.3. Центры шарниров кривошипа и шатуна лежат на одной прямой.

18.4. Отсутствие эксцентриситета при вращении кривошипа.

 

19. Какой закон движения толкателя в кулачковом механизме обеспечивает безударную работу?

19.1. Косинусоидальный закон

19.2. Синусоидальный закон

19.3. Закон постоянной скорости

19.4. Закон постоянного ускорения.

 

20. В каких механизмах существует подобие движений ведомых звеньев?

20.1. Кривошипно-ползунном и четырехзвенном

20.2. Кулисном и кулачковом 

20.3. Механизмом мальтийского креста и кулисном

20.4. Четырехзвенном и механизмом мальтийского креста

   

 

 

 

 

ВОПРОСЫ К ЗАЧЕТУ

 по курсу «Расчет и конструирование машин и аппаратов пищевых производств»

 

1. Задачи анализа и синтеза машин.

2. Общая классификация машин, основные признаки и подразделения.

3. Производительность машин непрерывного и периодического действия.

4. Классификация циклических машин, основные циклы и классы.

5. Машины-автоматы I-го класса, их разновидности, схемы и основные циклы

6. Машины-автоматы II-го класса, их разновидности, схемы и основные циклы

7. Машины-автоматы III-го класса, их разновидности, схемы и основные циклы

8. Основные виды циклограмм и методы их построения.

9. Синхронизация движения рабочих органов машин-автоматов.

10. В чем преимущество синхрограмм перед циклограммами интервалов?

11. Что понимают под законами движения рабочих органов?

12. Базисные механизмы машин-автоматов, определение и примеры.

13. Общие кинематические зависимости базисных механизмов.

14. Кривошипно-ползунный механизм, схема, законы движения ползуна, синхрограмма.

15. Кулисный механизм, схема, законы движения кулисы, синхрограмма.

16. Четырехзвенный механизм, схема, теорема Грасгофа, синхрограмма.

17. Механизм мальтийского креста, схема, законы движения креста, синхрограмма.

18. Кулачковые механизмы, схемы, основные законы движения центра ролика.

19. Метод построения профиля кулачка на заданные законы движения рабочего органа.

 

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Основы расчета и конструирования машин и автоматов пищевых производств. Под ред. Соколова А.Я. – М.: Машиностроение, 1969. – 639 с.

2. Артоболевский И.И. Теория Механизмов. – М.: Наука, 1979. – 640 с.

3. Белецкий В.Я. и др. Машины-автоматы и автоматические линии пищевой промышленности. – Киев: Техника, 1967. – 175 с.

4. Гернет М.М. Курс теоретической механики. – М.: Высшая школа, 1981.

5. Лунин О.Г. Поточные линии кондитерской промышленности. – М.: Пищевая промышленность, 1970. – 380 с.

6. Лунин О.Г., Вельтищев В.Н. Основы расчета и конструирования машин и аппаратов пищевых производств. Курс лекций. – М.: ВЗИПП, 1976. – 170 с.

7. Островский Э.В., Эйдельман Е.В. Краткий справочник конструктора продовольственных машин. – М.: Машиностроение, 1972.

8. Соколов А.Я. Транспортирующие и перегрузочные машины для комплексной механизации пищевых производств. – М.: Пищевая промышленность, 1964. – 759 с.

9. Харламов С.В. Конструирование технологических машин и аппаратов. Изд-во Ленинградского университета, 1974. – 272 с.

10. Шувалов В.Н. Машины-автоматы и поточные линии. – Л.: Машиностроение, 1973. – 543 с.

 

 

ОТВЕТЫ НА ТЕСТЫ

 

1.– 1.3; 2. – 2.2; 3. – 3.1; 4. – 4.4;

5. – 5.3; 6. – 6.1; 7. – 7.3;

8. – 8.3; 9. – 9.2; 10. – 10.3;

11. – 11.4; 12. – 12.5; 13. – 13.3;

14. – 14.1; 15. – 15.4; 16. – 16.2;

17. – 17.3; 18. – 18.1; 19. – 19.2; 20. – 20.3