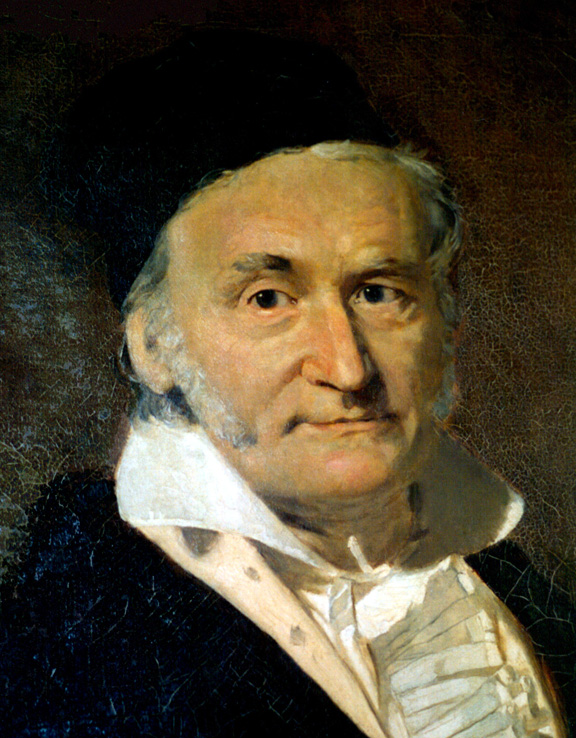Готфрид Лейбниц ( 1646 — 1716 гг.)

Этот немецкий учёный жил и творил в одно время с Ньютоном, и, независимо от последнего, создал основы математического анализа, опирающиеся на понятия бесконечно малых величин. Лейбниц представлял себе матанализ алгебраически, а не кинематически, как это делал Ньютон.

Леонард Эйлер (1707 — 1783 гг.)

В специальной литературе нередко можно встретить утверждение, что этот швейцарец является самым выдающимся математиком всех времён. Между прочим, он много лет прожил в России, в Петербурге, и даже многие свои работы написал на русском языке, который выучил в совершенстве всего за год!

Трудно найти отрасль математики, в которой Эйлер не написал бы хоть одну важную работу. Он впервые создал «математический оркестр», увязав множество доселе разрозненных дисциплин в единую систему математики. Язык современной математики нельзя представить без таких понятий, как «углы Эйлера» или «формула Эйлера». Некоторые математические вопросы до сегодняшнего дня преподают студентам «по Эйлеру».

Рене Декарт (1596 — 1650 гг.)

Когда мы говорили, что Ньютон и Лейбниц разработали основы математического анализа, справедливо было бы вспомнить, что их изыскания базировались не на пустом месте. Начальные идеи были известны ещё до работ этих учёных, а разработал их почти легендарный француз, Рене Декарт.

Современные математики считают его зачинателем аналитической геометрии. Он впервые ввёл понятия функции и переменной величины. С одним из достижений Декарта сталкивался практически каждый человек. Это система координат, известные всем шкалы «икс» и «игрек». Помимо этого, именно Рене ввёл в математику понятия гиперболы и параболы, овала и листа.

 

 

Жозеф Луи Лагранж (1736 — 1813 гг.)

В XVIII веке, наряду с Эйлером, этот француз считался лучшим европейским математиком. Был особенно силён в области математического синтеза. Разработал и доказал несколько важнейших теорем, в том числе «формулу конечных приращений».

Пьер-Симон Лаплас (1749 — 1827 гг.)

Много работал как астроном, но в математике известен как один из тех, кто разрабатывал теорию вероятностей. Специалистам известны уравнения его имени и преобразование Лапласа. Ввёл важное понятие математического ожидания.

Иоганн Гаусс (1777 — 1855 гг.)

Мы говорили уже об отце математики — Пифагоре. А этого немца нередко называют королём математики. Гаусс написал ряд важнейших работ во многих отраслях этой науки, которые до сих пор остаются базовыми, классическими. Много работал в математическом анализе, в неэвклидовой геометрии, открыл так называемые «гауссовые числа», разработал модель комплексных чисел.

Российские математики

В заключение хотелось бы подчеркнуть, что свой вклад, причём значительный, внесли в европейскую математическую науку и российские учёные. Вспомним хотя бы о некоторых их них.