
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Пусть AC и BD – диагонали параллелограмма ABCD. Самый простой способ – воспользоваться теоремой косинусов. Из треугольника BDC: Сложим полученные равенства:
Теорема косинусов помогает найти решение многих задач по планиметрии из вариантов ЕГЭ по математике.
4. Площадь выпуклого четырехугольника Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними.
Дан четырехугольник ABCD с диагоналями AC и BC, Четырехугольник ABCD разобьем на четыре треугольника (AOD,COD,BOC,BOA).
Площадь четырехугольника ABCD равна сумме площадей треугольников, на которые он разбивается диагоналями Так как
Полезное следствие. Диагонали ромба перпендикулярны, угол между ними равен Для ромба ABCD:
5. Свойства трапеции: отрезок, соединяющий середины диагоналей Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Пусть точка М – середина диагонали АС, N – середина диагонали ВD, Р и Q – середины боковых сторон АВ и СD. Задача ЕГЭ по теме: «Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований». Основания трапеции равны 10 и 6. Найдите отрезок, соединяющий середины диагоналей трапеции.
Проведем PQ – среднюю линию трапеции, PQ = 8. Как мы доказали, отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.
Тогда MN = PQ − PM − NQ = 8 − 3 − 3 = 2
6. Свойства равнобедренной трапеции Свойства равнобедренной трапеции
|
|||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.82.79 (0.004 с.) |

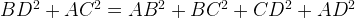 .
.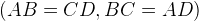 , поэтому равенство, которое нужно доказать, можно записать в виде:
, поэтому равенство, которое нужно доказать, можно записать в виде: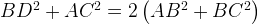 .
.
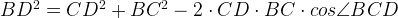

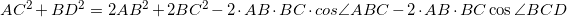
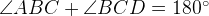 (как односторонние углы при параллельных сторонах AB и CD), поэтому
(как односторонние углы при параллельных сторонах AB и CD), поэтому  .
.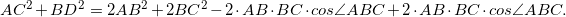
 , что и требовалось доказать.
, что и требовалось доказать.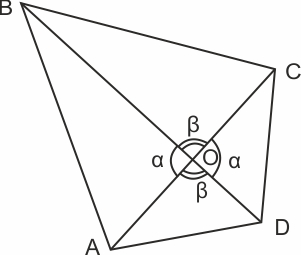
 .
.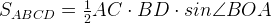 .
.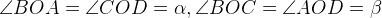 .
.
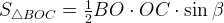
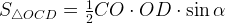
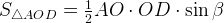
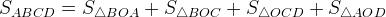
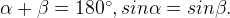
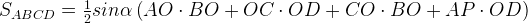
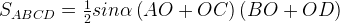
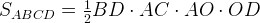
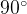 ,
,  .
.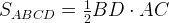

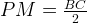 .
. . Поскольку
. Поскольку 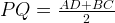 ,
, 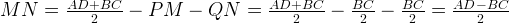 .
.



