
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ численного интегрирования при помощи программы
Методические указания
к лабораторной работе “ Численное интегрирование ”
Курган 2016 г. 1. Задание для лабораторной работы Написать программу для численного интегрирования функций на заданном промежутке. Реализовать метод прямоугольника, трапеции и Симпсона. Произвести сравнения этих методов.
К методическим указаниям приложен демонстрационный вариант лабораторной работы. 2. Введение
Численное интегрирование — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.
Численное интегрирование применяется, когда: Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки. Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, f(x) = exp(− x2). В этих двух случаях невозможно вычисление интеграла по формуле Ньютона-Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом. Задача численного интегрирования состоит в замене исходной подынтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). Такой функцией обычно является полином (кусочный полином)
Метод прямоугольников Различают метод левых, правых и средних прямоугольников. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс. Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = xi.
Рассмотрим диапазон интегрирования от xi до xi+h, где h – шаг интегрирования.
Вычислим = В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид
Здесь n – число разбиений интервала интегрирования, Метод средних прямоугольников. Здесь на каждом интервале значение функции считается в точке
Метод трапеций Аппроксимация в этом методе осуществляется полиномом первой степени. На единичном интервале
Особенности поведения погрешности. Казалось бы, зачем анализировать разные методы интегрирования, если мы можем достичь высокой точности, просто уменьшая величину
Метод Симпсона
Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла. Рассмотрим два шага интегрирования (h = const = xi+1 – xi), то есть три узла x0, x1, x2, через которые проведем параболу, воспользовавшись уравнением Ньютона:
В итоге
Здесь
СОДЕРЖАНИЕ
1. Задание для лабораторной работы....................…………………………...стр. 1 2. Введение ………………………………………………………………..…....стр. 2 3. Метод прямоугольников………………..……………………………….…..стр. 2 4. Метод трапеции…………………………..……………………………….…стр. 3 5. Метод Симпсона………………………..……………………………….…...стр. 4 6. Анализ численного интегрирования при помощи программы..………....стр. 6 7. Требования к программе………………………………………………….....стр. 9 8. Упражнения для практической работы………………………………….....стр. 10 9. Контрольные вопросы…………………………………………………….....стр. 11
Методические указания
к лабораторной работе “ Численное интегрирование ”
Курган 2016 г. 1. Задание для лабораторной работы Написать программу для численного интегрирования функций на заданном промежутке. Реализовать метод прямоугольника, трапеции и Симпсона. Произвести сравнения этих методов.
К методическим указаниям приложен демонстрационный вариант лабораторной работы. 2. Введение
Численное интегрирование — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.
Численное интегрирование применяется, когда: Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки. Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, f(x) = exp(− x2). В этих двух случаях невозможно вычисление интеграла по формуле Ньютона-Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом. Задача численного интегрирования состоит в замене исходной подынтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). Такой функцией обычно является полином (кусочный полином)
Метод прямоугольников Различают метод левых, правых и средних прямоугольников. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.
Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = xi.
Рассмотрим диапазон интегрирования от xi до xi+h, где h – шаг интегрирования. Вычислим = В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид
Здесь n – число разбиений интервала интегрирования, Метод средних прямоугольников. Здесь на каждом интервале значение функции считается в точке
Метод трапеций Аппроксимация в этом методе осуществляется полиномом первой степени. На единичном интервале
Особенности поведения погрешности. Казалось бы, зачем анализировать разные методы интегрирования, если мы можем достичь высокой точности, просто уменьшая величину
Метод Симпсона
Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла. Рассмотрим два шага интегрирования (h = const = xi+1 – xi), то есть три узла x0, x1, x2, через которые проведем параболу, воспользовавшись уравнением Ньютона:
В итоге
Здесь
Анализ численного интегрирования при помощи программы
Сравним методы численного интегрирования, проинтегрировав функцию 4*cos(x)*cos(4*x)-sin(x)*sin(4*x)
Зададим максимальную относительную погрешность 0,1 и интервал [1;2]:
Как мы видим, метод прямоугольников использует наибольшее число итераций и занимает наибольшее количество времени. Метод Симпсона использует наименьшее число итераций и занимает меньше времени, чем метод трапеций.
Увеличим точность 0,01 и предел интегрирования [1;3]
Метод прямоугольников использует наибольшее число итераций и занимает наибольшее количество времени. Метод Симпсона использует наименьшее число итераций и занимает меньшее количество времени по сравнению с методом трапеций.
Установим количество итераций равным 4 на промежутке интегрирования [1;2] и сравним показатели методов интегрирования:
Как мы видим, при равном количестве итераций самую высокую точность показал метод Симпсона, а самую низкую – метод прямоугольников. Время приблизительно одинаковое, однако трапеция имеет наименьшее время
Вывод: Метод прямоугольников во всех исследованиях показал наихудший результат, однако он наиболее прост в реализации. Метод трапеций и метод Симпсона дают наилучший результат при сравнительно одинаковом количестве времени, но метод трапеций проще в реализации, а метод Симпсона использует меньшее количество итераций. 7. Требования к программе
|
||||||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.131.168 (0.059 с.) |
 . То есть:
. То есть: ,
,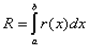 – априорная погрешность метода на интервале интегрирования,
– априорная погрешность метода на интервале интегрирования,  …
… …=
…= =
=  . Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.
. Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности. .
. . Для справедливости существования этой оценки необходимо существование непрерывной f'(x).
. Для справедливости существования этой оценки необходимо существование непрерывной f'(x). , то есть
, то есть  . Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:
. Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:
 .
.
 , а
, а 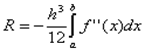 . Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.
. Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками. шага интегрирования. Однако рассмотрим график поведения апостериорной погрешности R результатов численного расчета в зависимости от числа n разбиений интервала (то есть при
шага интегрирования. Однако рассмотрим график поведения апостериорной погрешности R результатов численного расчета в зависимости от числа n разбиений интервала (то есть при  шаг
шаг  . На участке (1) погрешность уменьшается в связи с уменьшением шага h. Но на участке (2) начинает доминировать вычислительная погрешность, накапливающаяся в результате многочисленных арифметических действий. Таким образом, для каждого метода существует своя Rmin, которая зависит от многих факторов, но прежде всего от априорного значения погрешности метода R.
. На участке (1) погрешность уменьшается в связи с уменьшением шага h. Но на участке (2) начинает доминировать вычислительная погрешность, накапливающаяся в результате многочисленных арифметических действий. Таким образом, для каждого метода существует своя Rmin, которая зависит от многих факторов, но прежде всего от априорного значения погрешности метода R.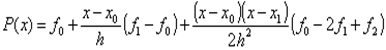 .
.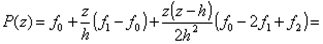
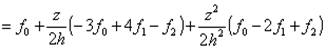
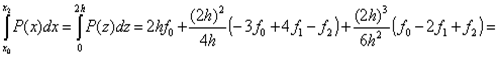
 .
.
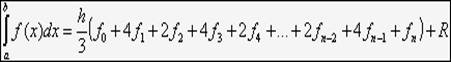
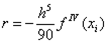 , а
, а  в предположении непрерывности четвертой производной подынтегральной функции.
в предположении непрерывности четвертой производной подынтегральной функции.





