
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоретические сведения. Ранее были рассмотрены условия распространения тепла при стационарном режимеСодержание книги
Поиск на нашем сайте
Ранее были рассмотрены условия распространения тепла при стационарном режиме, когда температурное поле во времени не менялось, оставаясь постоянным. Такие процессы теплопроводности, когда поле температуры в теле изменяется не только в пространстве, но и во времени, называются нестационарными. Среди практических задач нестационарной теплопроводности важное значение имеют две группы процессов: а) тело стремится к тепловому равновесию; б) температура тела претерпевает периодические изменения. К первой группе относятся процессы нагрева или охлаждения тел, помещенных в среду с заданным тепловым состоянием. Ко второй группе относятся процессы в периодически действующих подогревателях. В условиях передачи тепла через стенку при внезапном изменении температуры одного из теплоносителей не все тепло будет передаваться через стенку: часть его уйдет на изменение внутренней энергии самой стенки (ее температуры), и только при наступлении стационарного процесса все тепло будет передаваться через стенку от одной жидкости к другой. При внесении тела в среду с постоянной температурой по мере нагрева (охлаждения тела) температура в каждой точке тела будет асимптотически приближаться по времени к температуре окружающей среды. Эти примеры указывают на то, что нестационарные тепловые процессы всегда связаны с изменением внутренней энергии или энтальпии вещества. Так как скорость изменения энтальпии прямо пропорциональна способности материала проводить тепло (т.е. коэффициенту теплопроводности λ) и обратно пропорциональна его аккумулирующей способности (т.е. объемной теплоемкости сρ), то в целом скорость теплового процесса при нестационарном режиме теплопроводности определяется значением коэффициента температуропроводности Рассмотрим лишь несколько важных задач, относящихся к процессам, в которых тело стремится к тепловому равновесию. Для более широкого ознакомления с решениями большого круга задач нестационарной теплопроводности как в случаях стремления температуры тела к состоянию равновесия, так и ее периодического изменения, следует обратиться к специальной литературе /2, 4, 10, 14, 15, 21-28, 30, 32, 33/.Ниже в таблице приведены постановка и решения задач нестационарной теплопроводности для полуограниченного тела (задачи 1-3), неограниченной пластины (задачи 4-9), неограниченного цилиндра (задачи 10-12) и шара (задачи 13-15).
Дифференциальные уравнения теплопроводности в предложенных задачах имеют вид: для полуограниченного тела и неограниченной плоской пластины:
для неограниченного цилиндра:
для шара:
В выражениях (4.1 ÷ 4.3) t – температура тела, x, r – координаты распространения тепла, τ – время процесса. Условия однозначности, тепловые схемы и решения задач в критериальном виде приведены также в этой таблице. Относительно решения задач нестационарной теплопроводности следует отметить, что после выбора тепловой схемы задачи и назначения начальных и граничных условий требуемая задача может быть решена аналитически (или графически /30/) по предложенным выражениям. В полученных решениях критерий Фурье В задачах с граничными условиями третьего рода, кроме Fo и h, добавляется еще одна независимая переменная – критерий Био
4.2 Задачи для самостоятельного решения.
1. Скальное основание (а=0,53 × 10-2 м2/ч) к моменту ввода сооружения в эксплуатацию имело температуру t 0 = - 7 ° C. В дальнейшем температура на поверхности стала равной tn = 10 ° C. Найти температуру и градиент температуры на глубине 1м через 1месяц.
2. Большой плоский слиток меди (а=0,41 м2/ч, l =382 Вт/м × град), имевший температуру t 0 = 20 ° C, нагревается с одной из поверхностей постоянным тепловым потоком S =5000 Вт/м2. Вторая поверхность теплоизолирована и столь отдалена, что на ней сохраняется начальная температура. Найти среднюю температуру в слое 0 – 25 см. и температуру на нижней границе этого слоя через 30 мин. 3. Фундамент металлургической печи (а=0,0025 м2/ч, l =1,4 Вт/м × град), имевший в начальный момент температуру t 0 = 20 ° C, разогревается при постоянной температуре воздуха в печи J = 300 ° C, причем коэффициент теплообмена 4. Плоский слиток металла (а=0,053 м2/ч) толщиной h = 0,1м прогрет до температуры t 0 = 500 ° C. Затем одна поверхность слитка поддерживается при температуре tn = 70 ° C, на другой поверхности теплоотвод пренебрежительно мал. Найти температуру и градиент температуры в центре слитка через 10 мин после начала охлаждения. 5. Бронзовый слиток (l =64 Вт/м × град, а=0,075 м2/ч) толщиной h = 20 см нагревается с одной из поверхностей в течении 12 мин постоянным тепловым потоком S =25000 Вт/м2. Вторая поверхность теплоизолирована. Температура слитка до нагрева составляла t 0 = 120 ° C. Найти температуру слитка и градиент температуры на расстоянии 5см от подогреваемой поверхности через 12 мин. 6. Железобетонная стенка здания (l = 1,56 Вт/м × град, а = 0,003 м2/ч) толщиной h = 50 см имеет температуру t 0 = 15 ° C. Наружная поверхность стены подвергается нагреву постоянным тепловым потоком S = 325 Вт/м2, на внутренней поверхности сохраняется начальная температура. Найти время, по прошествии которого средняя температура стенки станет равной 7. Шамотная плита (l =0,7 Вт/м × град, а=0,0167 м2/ч) толщиной h = 30см имеет начальную температуру, равную температуре среды: t 0 = J = 45 ° C. В дальнейшем плита подвергается одностороннему нагреву постоянным тепловым потоком S = 700 Вт/м2. Коэффициент теплообмена a = 7,0 Вт/м2 × град. Найти среднюю температуру в плите и градиент температуры на средней плоскости плиты через 5 ч после включения подогрева. 8. Латунная пластина (l = 85,5 Вт/м × град, а = 0,0114 м2/ч) толщиной 9. Кирпичная стена здания (l =0,81 Вт/м × град, а=0,002 м2/ч) толщиной 10 Стальной цилиндр (а = 0,04 м2/ч) диаметром 2 R = 40см после нагрева до температуры t 0 = 400 ° C погружен в проточную воду при температуре tn = 60 ° C, причем предполагается, что температура на поверхности цилиндра равна температуре воды. Найти температуру на расстоянии 15 см от центра цилиндра через 11 Длинный цилиндр (l = 25 Вт/м × град, а = 0,05 м2/ч) диаметром
12 Стальной вал (l = 58 Вт/м × град, а = 0,053 м2/ч) радиусом R = 0,3м, имевший температуру t 0 = 100 ° C, загрузили в печь с температурой J = 400 ° C Теплообмен между поверхностью вала и воздухом в печи происходит по закону конвекции, причем a = 97 Вт/м2 × град. Найти среднюю температуру вала через 36 мин после загрузки в печь. 13 Образец испытуемого материала выполнен в виде шара диаметром 14 Железный шар (l = 78,4 Вт/м × град, а = 0,08 м2/ч) диаметром
15 Стальной шар (l = 51 Вт/м × град, а = 0,046 м2/ч) имеет температуру 5 ОБОБЩЕНИЕ ОПЫТНЫХ ДАННЫХ И НАХОЖДЕНИЕ
При постановке любого эксперимента всегда необходимо заранее знать: 1. какие величины надо измерить в опыте; 2. как обрабатывать результаты опыта; 3. какие явления подобны изучаемому.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.123.197 (0.011 с.) |

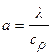 , который здесь имеет такое же важное значение, как и коэффициент теплопроводности при стационарном режиме распространения тепла.
, который здесь имеет такое же важное значение, как и коэффициент теплопроводности при стационарном режиме распространения тепла.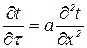 ; (4.1)
; (4.1)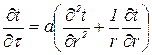 ; (4.2)
; (4.2)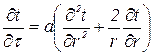 . (4.3)
. (4.3)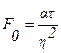 представляет собой относительное безразмерное время процесса. В нем сопоставлено текущее время τ и группа величин
представляет собой относительное безразмерное время процесса. В нем сопоставлено текущее время τ и группа величин 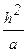 , имеющая размерность времени и характеризующая скорость перестройки температурного поля в теле. Отношение
, имеющая размерность времени и характеризующая скорость перестройки температурного поля в теле. Отношение 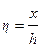 является безразмерной координатой.
является безразмерной координатой.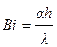 . Здесь a –коэффициент теплообмена внешней среды и тела, λ - коэффициент теплопроводности тела, h – определяющий размер тела: для пластины - толщина, для полуограниченного тела – глубина и т.д. Отношение внутреннего и внешнего тепловых сопротивлений, соответственно
. Здесь a –коэффициент теплообмена внешней среды и тела, λ - коэффициент теплопроводности тела, h – определяющий размер тела: для пластины - толщина, для полуограниченного тела – глубина и т.д. Отношение внутреннего и внешнего тепловых сопротивлений, соответственно 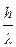 и
и  , называется критерием В i:
, называется критерием В i: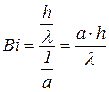 . (4.4)
. (4.4)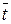 = 40°C.
= 40°C.


