Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Счетчики с произвольным коэффициентом пересчетаСодержание книги Поиск на нашем сайте
(Слайд) Двоично-кодированные счетчики с произвольным модулем счета также называют счетчиками с произвольным коэффициентом пересчета. Коэффициентом пересчета называют максимальное число, которое можно записать в этот счетчик. Все ранее рассмотренные счетчики имели коэффициент пересчета, равный Нередко на практике в цифровой технике необходимо создавать счетчики с модулями, отличным от Счетчики с произвольным коэффициентом пересчета называются пересчетными устройствами, а счетчики с коэффициентом пересчета (Слайд) Принцип построения декадного счетчика заключается в исключении у счетчика лишних состояний Потребное количество разрядов счетчика должно удовлетворять следующему условию
Для (Слайд) Таблица 19.3 – Таблица истинности для декадного счетчика
Для построения счетчика с произвольным модулем
Число (Слайд) Наибольшее распространение на практике при построении таких счетчиков получил метод управляемого сброса. Для реализации данного алгоритма пригоден любой двоичный счетчик, имеющий входы сброса и начальной установки. Идея метода состоит в принудительном формировании сигнала сброса триггеров разрядных схем двоичного счетчика при появлении на его выходе кода, совпадающим с требуемым модулем счета
Анализ данных таблицы 19.3 показывает, что нужна логическая схема, которая по приходу десятого импульса переводит счетчик в нулевое (начальное) состояние. Переключательная функция
Функциональная схема десятичного счетчика, удовлетворяющего таблице истинности (см. таблицу 19.3), показана на рисунке 19.8.
Рисунок 19.8 – Функциональная схема десятичного счетчика на JK -триггерах
Рассмотрим схему представленную на рисунке 19.8. Четырехразрядный двоичный счетчик имеет дополнительно 4-х входовый элемент 4И-НЕ, на входы которого подаются сигналы с выходов триггера
что соответствует Тогда элемент 4И-НЕ через время, равное задержке распространения сигнала формирует на своем выходе нулевой сигнал сброса, который» поступая на асинхронные входы Временные диаграммы, иллюстрирующие работу десятичного счетчика, представлены на рисунке 19.9. (Слайд)
Рисунок 19.9 – Временные диаграммы десятичного счетчика
Решение задачи управляемого сброса можно упростить. Например, при формировании двоично-десятичного счетчика обратим внимание, что единичные выходы берут с двух разрядов – первого и третьего. Тогда можно использовать двухвходовый элемент 2И-НЕ, подовая на его входы сигналы Таким образом, если все оставшиеся наборы двоичных кодов (11, 12, 13, 14 и 15) принять равными 1, то выражение может быть приведено к виду:
а его реализация предполагает коммутацию прямых выходов тех триггеров, которые достигают единичного значения к моменту прихода десятого импульса. По такому принципу строится десятичный счетчик на микросхеме К555ИЕ5, имеющий два входа асинхронного сброса
(Слайд)
Рисунок 19.10 – Микросхемы десятичных счетчиков: а) К555ИЕ5; б) К555ИЕ9
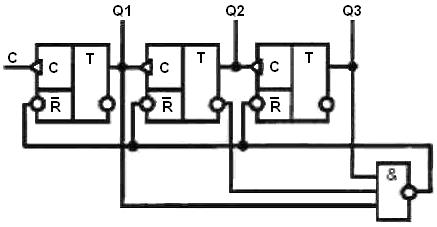
Ввидуособой важности десятичных счетчиков в стандартных сериях микросхем имеются другие десятичные счетчики. Например, микросхема К555ИЕ9 (рисунок 19.10 б) – четырехразрядный двоично-десятичный счетчик с асинхронным сбросом, дешифрирующим счетным выходом, с возможностью синхронной установки с произвольное состояние от нуля до девяти. Счетчик имеет вход синхронизации Для переноса импульса в следующий каскад предусмотрена специальная схема с входом разрешения переноса Аналогичным образом могут быть построены счетчики на любое другое значение модуля счета. Например, для построения счетчика по модулю 5 необходимо три триггера На входы элемента 3И-НЕ подаются сигналы (Слайд)
Рисунок 19.11 – Пример счетчика по модулю М=5
Таким образом, построение счетчика с заданным коэффициентом пересчета производится в соответствии с общей методикой синтеза цифровых автоматов, на основе анализа логики его работы, описанной в виде таблицы истинности. Отметим, что среди счетчиков с недвоичным кодированием практическое значение имеют счетчики с кодом Грея, счетчики Джонсона, счетчики с кодом «1 на N».
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 1485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.113 (0.007 с.) |

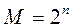 , где
, где 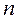 – количество разрядов в счетчике.
– количество разрядов в счетчике.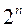 , т. е счетчики с произвольным модулем. Из них наиболее часто встречаются двоично-десятичные счетчики с модулем счета
, т. е счетчики с произвольным модулем. Из них наиболее часто встречаются двоично-десятичные счетчики с модулем счета 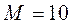 , поскольку десятичная система счисления является общепринятой.
, поскольку десятичная система счисления является общепринятой.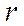 , число которых
, число которых 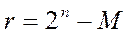 .
.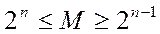
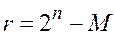 (
(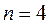 , т. е. для счетчика натуральных десятичных чисел необходим четырехразрядный двоичный счетчик с особой логикой работы. Схемная логика его отличается тем, что сброс в нуль происходит на каждом десятом входном сигнале. Ниже приведена таблица истинности для такого счетчика (таблица 19.3).
, т. е. для счетчика натуральных десятичных чисел необходим четырехразрядный двоичный счетчик с особой логикой работы. Схемная логика его отличается тем, что сброс в нуль происходит на каждом десятом входном сигнале. Ниже приведена таблица истинности для такого счетчика (таблица 19.3).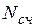
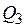
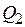
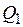
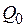
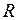
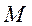 может использоваться также следующая формула
может использоваться также следующая формула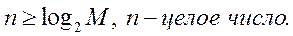
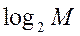 округляют до ближайшего большего целого числа. В результате получаем число необходимых триггеров.
округляют до ближайшего большего целого числа. В результате получаем число необходимых триггеров.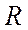 для такой схемы равна:
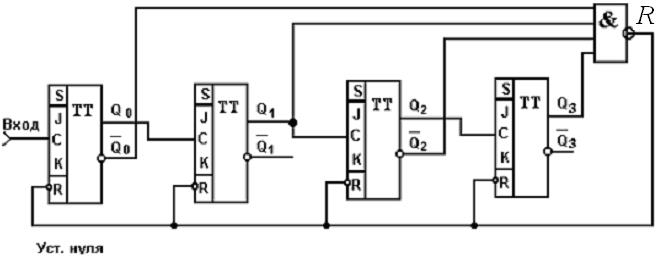
для такой схемы равна: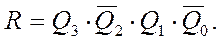
 .При появлении на синхронизирующем входе
.При появлении на синхронизирующем входе 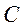 одиннадцатого по счету импульса триггера счетчика устанавливаются в состояние 1010, т. е.:
одиннадцатого по счету импульса триггера счетчика устанавливаются в состояние 1010, т. е.: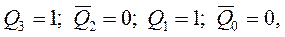
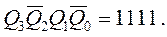
 всех триггеров, принудительно устанавливает их в нулевое состояние. Далее начинается новый цикл счета.
всех триггеров, принудительно устанавливает их в нулевое состояние. Далее начинается новый цикл счета.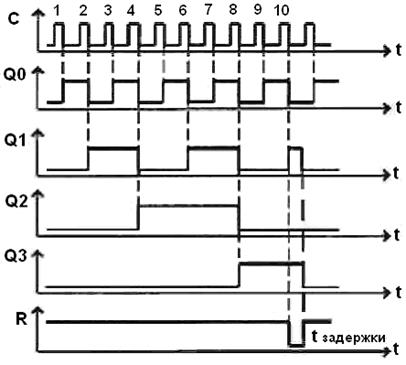
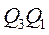 , а инверсные выходы с нулевого и второго разрядов счетчика
, а инверсные выходы с нулевого и второго разрядов счетчика 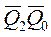 не использовать.
не использовать.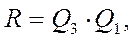
 и
и 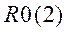 (рисунок 19.10 а), объединенных операцией И-НЕ. Для выполнения десятичного счета достаточно входы
(рисунок 19.10 а), объединенных операцией И-НЕ. Для выполнения десятичного счета достаточно входы 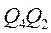 .
.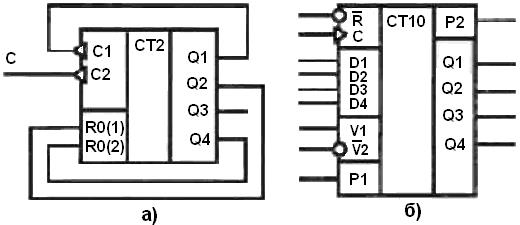
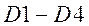 , входы разрешения счета
, входы разрешения счета 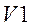 , разрешения предварительной записи
, разрешения предварительной записи 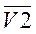 , разрешения переноса
, разрешения переноса 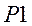 , четыре выхода
, четыре выхода 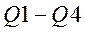 и выход переноса информации
и выход переноса информации 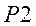 .
.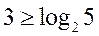 . На рисунке 19.11 показан пример счетчика по модулю 5.
. На рисунке 19.11 показан пример счетчика по модулю 5.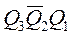 в соответствии с 510 = 101,. Далее по приходу пятого импульса на выходе элемента 3И-НЕ формируется кулевой уровень, который обнуляет счетчик, поступая на входы асинхронного сброса
в соответствии с 510 = 101,. Далее по приходу пятого импульса на выходе элемента 3И-НЕ формируется кулевой уровень, который обнуляет счетчик, поступая на входы асинхронного сброса