Обещает стать наиболее важным
Н. Винер
Трудно найти такую сферу человеческой деятельности, в которой не использовались бы вероятностно-статистические методы. Они применяются практически во всех областях науки, в экономике, военном деле, технике, медицине, криминалистике и т.д.
Эти методы базируются на понятиях
случайного события и вероятности.
Решающий вклад в теорию вероятностей внесли такие замечательные математики как
Пьер Ферма,
Якоб Бернулли,
Симон Лаплас,
Пафнутий Львович Чебышев,
Андрей Николаевич Колмогоров
и многие другие.
Блез Паскаль - франц. ученый XVІІ в., один из первых исследователей случайного, обратил внимание на парадоксальность сочетания слов теория и вероятность.
В своем письме в Парижскую академию наук в 1654 году он писал:
«И так как строгость научных доказательств сочетается здесь с неопределенностью случайности, то трактат, где эти два предмета, с виду противоположные, как бы примирились друг с другом, может по праву претендовать на ошеломляющее название " Математика случая "».
Считается, что к выводу о существовании строгих законов, описывающих случайные явления, Паскаль пришел в результате размышлений над двумя задачами, которые поставил перед ним известный игрок шевалье де Мере.
************************
Задачи де Мере.
Первая задача де Мере.
Что вероятнее: при 4 бросаниях одной игральной кости хотя бы раз получить 6 очков или при 2-х бросаниях двух костей хотя бы раз получить 12 очков?
Вторая задача де Мере.
Два игрока, одинаково искусных, договорились сыграть серию в несколько партий с условием, что приз получает тот из них, кто первым выиграет пять партий. По правилам игры каждая партия заканчивается поражением одного из игроков.
Турнир был прерван, когда один из участников выиграл 4 партии, а другой – 3. Тем самым были сыграны 7 партий, и никто из игроков не успел набрать необходимого для победы. Как следует разделить приз между игроками?
********************
Обращение к азартным играм вовсе не случайно. Законы исчисления вероятностей обнаруживаются только при большом числе однотипных случайных испытаний,
при многократном повторении опыта.
Такими простыми и многократно повторяющимися опытами как раз и явились азартные игры в карты и кости, широко распространенные в Европе в XVІ – XVІІ веках. О них писали и Дж. Кардано, и Г. Галилей, и Х. Гюйгенс.
Азартными играми увлекались и в России.
Что ни толкуй
Волтер или Декарт –
Мир для меня – колода карт,
Жизнь – банк, рок мечет – я играю,
И правила игры я к людям
применяю.
М.Ю. Лермонтов
Однако рассчитывать меру надежды
пытаются не только игроки.
«Замечательно, что наука, которая
начала с рассмотрения азартных игр,
Обещает стать наиболее важным
объектом человеческого знания …
Ведь большей частью
важнейшие жизненные вопросы
являются на самом деле
задачами из теории вероятностей».
П.Лаплас
Независимыми
и несовместными
при одном испытании.
ПР 1. Испытание: подбрасывание монеты.
Событие А – выпадение герба, событие 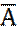 – выпадение цифры. – выпадение цифры.
?? Является ли это испытание схемой Бернулли?
Р(А)= p = 1/2, Р(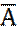 )= q = 1 – p = 1/2. )= q = 1 – p = 1/2.
?? Какова вероятность того, что при 5 бросках герб выпадет 2 раза?
?? Какова вероятность того, что при 7 бросках герб выпадет 3 раза?
?? Какова вероятность того, что
при n бросках герб выпадет m раз?
ПР 2. Испытание: стрельба по мишени.
Событие А – поражение цели, событие 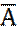 – промах. – промах.
?? Является ли это испытание схемой Бернулли?
Пусть для некоторого стрелка
Р(А) = p = 0.8, тогда
Р(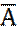 ) = q = 1 – p = 1 – 0.8 = 0.2 ) = q = 1 – p = 1 – 0.8 = 0.2
?? Какова вероятность того, что при 5 выстрелах цель будет поражена 2 раза?
?? Какова вероятность того, что при 7 выстрелах цель будет поражена 6 раз?
?? Какова вероятность того, что
при n выстрелах цель будет поражена m раз?
Выведем ФОРМУЛУ для вычисления
такой вероятности.
Допустим, эксперимент проведен n раз.
Вычислим P n (m) – вероятность того, что
при n испытаниях событие A наступит ровно m раз
(тогда остальные (n – m) раз наступит событие 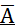 ). ).
Сначала выберем m испытаний из n и зафиксируем их номера. Мы знаем, что количество всех способов выбора m испытаний из n равно 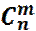 . .
Вычислим вероятность того, что
при каждом из этих m испытаний произошло событие А,
а в остальных n – m испытаниях – событие 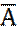 : :
если Р(А) = p,
а Р(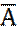 ) = q = 1 – p, ) = q = 1 – p,
то по теореме умножения для независимых испытаний
она равна 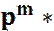 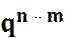 . .
Учтем, что количество всех способов выбора
m испытаний из n равно 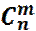 . .
Тогда по теореме сложения вероятностей
искомая вероятность Pn (m) будет равна
сумме только что вычисленных вероятностей
для всех способов выбора m испытаний из n.
Таким образом,
Pn (m) = 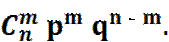
Эта формула называется формулой Бернулли.
С её помощью вычисляется P n (m) – вероятность того, что
при n испытаниях событие A наступит ровно m раз
(тогда остальные (n – m) раз наступит событие 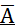 ). ).
ПР 1. Испытание: подбрасывание монеты.
Событие А – выпадение герба, событие 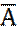 – выпадение цифры. – выпадение цифры.
Р(А)= p = 1/2, q = 1 – p = 1/2.
1) Монету подбрасывают 5 раз. Какова вероятность того, что при 5 бросках герб выпадет 2 раза?
n = 5, m = 2, p = 0.5, q = 0.5
P5 (2) = 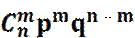 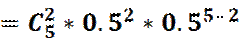 = =
= (5*4)/2* (1/2)5 = 10/25 = 5/16.
2) Монету подбрасывают 7 раз. Какова вероятность того, что при 7 бросках герб выпадет 3 раза?
n =7, m = 3, p = 0.5, q = 0.5,
P7 (3) = 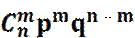 = =
= 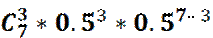 = =
= ………………………. =
= 35/128
3) Что вероятнее: выпадение 2 гербов при 5 бросках
или 3 гербов при 7 бросках?
(что больше: 5/16 или 35/128?)
....................................................................
4) Что вероятнее: выпадение 2 гербов при 5 бросках
или 3 цифр при 5 бросках?
Их вероятности равны.
5) Монету подбрасывают 6 раз.
· Найти вероятность того, что
герб выпадет не более 2-х раз.
n =6, «не более 2-х раз» означает: или 2 раза, или 1 раз, или ни разу(0 раз), т.е. m 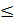 2. 2.
P 6 (m 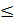 2) = 2) =
= P 6 (0) + P 6 (1) + P 6 (2) =
… =
= 1/26 + 6/ 26 + 15/ 26 =
=22/64 = 11/32
· Найти вероятность того, что герб выпадет более 2-х раз (от 3-х до 6-ти раз).
n =6, m > 2.
Какими будут события:
"герб выпадет не более 2-х раз " и
"герб выпадет более 2-х раз "?
Эти события противоположны, поэтому
P 6 (m > 2) = 1 - P 6 (m 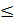 2) = 1 – 11/32 = 21/32 2) = 1 – 11/32 = 21/32
ПР 2. Испытание: стрельба по мишени.
Событие А – поражение цели, событие 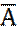 – промах. – промах.
Пусть для некоторого стрелка Р(А)= p = 0.8,
тогда Р(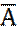 )= 1 – p = q = 1 – 0.8 = 0.2 )= 1 – p = q = 1 – 0.8 = 0.2
1) Какова вероятность того, что при 5 выстрелах цель будет поражена 2 раза?
n =..., m =..., p =..., q =...
P 5 (2) =  = =
=……………………=
=(5*4)/2*0.64* 0.008=
= 6.4*0.008 = 0.0512 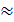 0.05 0.05
2) Какова вероятность того, что при 7 выстрелах цель будет поражена 6 раз?
n =, m =, p =, q =
P 7 (6) =  = =
= ……………… =
= 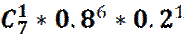 = =
= ……………… =
= 7* 0.0524288 = 0.3670016 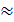 0.37. 0.37.
ПР 3. Испытание: стрельба по мишени.
Событие А – поражение цели, событие 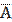 – промах. – промах.
Пусть для некоторого стрелка Р(А)= p = 2/3,
тогда Р(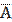 )= 1 – p = q = 1 –2/3= 1/3 )= 1 – p = q = 1 –2/3= 1/3
1) Какова вероятность того, что при 6 выстрелах попадание произойдет 4 раза?
n =, m =, p =, q =
P6 (4) = 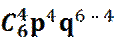 = =
=(6*5)/2* 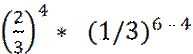 = =
= ……………………… = 80/243 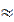 0.33. 0.33.
2) Какова вероятность того, что при 6 выстрелах попадание произойдет не меньше 3-х раз, но не больше 4-х раз?
n =, p =, q =
m -?
P 6 (3 ≤ m ≤ 4) =
= P 6 (3) + P 6 (4) =
= ………...........=
= (160 + 240)/729 =
= 400/729 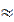 0.55 0.55
ПР. 4. Производится 8 выстрелов по цели, в каждом из которых вероятность попадания в цель равна 0.1. Для разрушения цели требуется хотя бы два попадания. Найти вероятность того, что цель будет разрушена.
Событие А – попадание в цель, событие 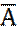 – промах. p = ____, q = ____ – промах. p = ____, q = ____
Н. Винер
Трудно найти такую сферу человеческой деятельности, в которой не использовались бы вероятностно-статистические методы. Они применяются практически во всех областях науки, в экономике, военном деле, технике, медицине, криминалистике и т.д.
Эти методы базируются на понятиях
случайного события и вероятности.
Решающий вклад в теорию вероятностей внесли такие замечательные математики как
Пьер Ферма,
Якоб Бернулли,
Симон Лаплас,
Пафнутий Львович Чебышев,
Андрей Николаевич Колмогоров
и многие другие.
Блез Паскаль - франц. ученый XVІІ в., один из первых исследователей случайного, обратил внимание на парадоксальность сочетания слов теория и вероятность.
В своем письме в Парижскую академию наук в 1654 году он писал:
«И так как строгость научных доказательств сочетается здесь с неопределенностью случайности, то трактат, где эти два предмета, с виду противоположные, как бы примирились друг с другом, может по праву претендовать на ошеломляющее название " Математика случая "».
Считается, что к выводу о существовании строгих законов, описывающих случайные явления, Паскаль пришел в результате размышлений над двумя задачами, которые поставил перед ним известный игрок шевалье де Мере.
************************
Задачи де Мере.
Первая задача де Мере.
Что вероятнее: при 4 бросаниях одной игральной кости хотя бы раз получить 6 очков или при 2-х бросаниях двух костей хотя бы раз получить 12 очков?
Вторая задача де Мере.
Два игрока, одинаково искусных, договорились сыграть серию в несколько партий с условием, что приз получает тот из них, кто первым выиграет пять партий. По правилам игры каждая партия заканчивается поражением одного из игроков.
Турнир был прерван, когда один из участников выиграл 4 партии, а другой – 3. Тем самым были сыграны 7 партий, и никто из игроков не успел набрать необходимого для победы. Как следует разделить приз между игроками?
********************
Обращение к азартным играм вовсе не случайно. Законы исчисления вероятностей обнаруживаются только при большом числе однотипных случайных испытаний,
при многократном повторении опыта.
Такими простыми и многократно повторяющимися опытами как раз и явились азартные игры в карты и кости, широко распространенные в Европе в XVІ – XVІІ веках. О них писали и Дж. Кардано, и Г. Галилей, и Х. Гюйгенс.
Азартными играми увлекались и в России.
Что ни толкуй
Волтер или Декарт –
Мир для меня – колода карт,
Жизнь – банк, рок мечет – я играю,
И правила игры я к людям
применяю.
М.Ю. Лермонтов
Однако рассчитывать меру надежды
пытаются не только игроки.
«Замечательно, что наука, которая
начала с рассмотрения азартных игр,
обещает стать наиболее важным
объектом человеческого знания …
Ведь большей частью
важнейшие жизненные вопросы
являются на самом деле
задачами из теории вероятностей».
П.Лаплас
|