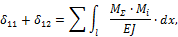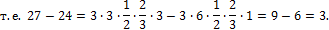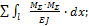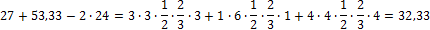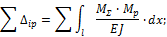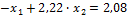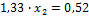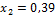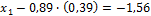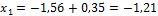Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3.8. Основы расчета статически неопределимых систем методом силСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Раздел 3 СТАТИКА СООРУЖЕНИЙ Тема 3.8. Основы расчета статически неопределимых систем методом сил
Статически неопределимая система Статически неопределимыми называют системы, в которых для определения опорных реакций либо внутренних усилий одних только уравнений статики недостаточно. Статическая неопределимость возникает из-за наличия дополнительных или «лишних» связей. Здесь под словом «лишние» понимаются дополнительные опоры (связи) добавление которых не влияет на геометрическую неизменяемость системы в целом. Дополнительные опоры увеличивают прочность и жесткость систем, что позволяет делать их более экономичными. Статически неопределимые системы обладают рядом характерных особенностей: 1. Статически неопределимая система ввиду наличия добавочных лишних связей, по сравнению с соответствующей статически определимой системой оказывается более жесткой. 2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках. 3. Разрушение лишних связей в нагруженном состоянии, не ведет к разрушению всей системы в целом, так как удаление этих связей приводит к новой геометрически неизменяемой системе, в то время как потеря связи в статически определимой системе приводит к изменяемой системе. 4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы. 5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости. 6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий. Примеры статически неопределимых систем
Рис. 8.1 Рис. 8.2 Рис. 8.3
Консольная балка (рис. 8.1), закрепленная только в жесткой заделке – статически определима, так как в опоре данной схемы могут иметь место не более трех опорных реакций (вертикальная и горизонтальная силы и момент(рис. 8.2)). Как известно из курса теоретической механики для плоской системы сил можно составить только три уравнения равновесия. Трех уравнений для определения трех неизвестных вполне достаточно. Теперь, если добавим к рассматриваемой схеме еще одну опору (рис. 8.3), например шарнирно-подвижную, то балка становится статически неопределимой, так как количество неизвестных связей увеличилось до четырех, а уравнений равновесия по-прежнему можно составить только три. В данном случае для расчета опорных реакций не хватает еще одного уравнения, т.е. система один раз (однажды) статически неопределима. Если к данной системе последовательно добавлять опоры, то степень неопределимости также будет возрастать. В таких случаях для расчета величины и направления неизвестных усилий потребуются дополнительные уравнения. Другие примеры статически неопределимых систем Примеры однажды статически неопределимых систем (n=1):
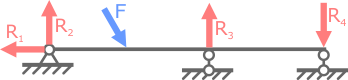
Рис. 8.4 Статически неопределимый стержень Рис. 8.5 Трехопорная балка
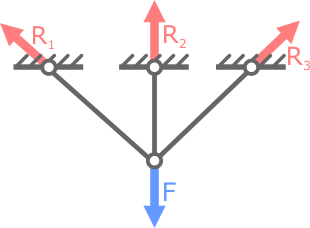
Рис. 8.6 Статически неопределимая стержневая система
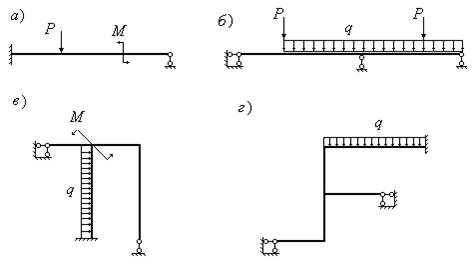
На рис. 8.7 приведены примеры статически неопределимых балок и рам.
Рис. 8.7
Балка, изображенная на рис. 8.7, б, называется неразрезной балкой. Происходит это название оттого, что промежуточная опора лишь подпирает балку. В месте опоры балка не разрезана шарниром, шарнир не врезан в тело балки. Поэтому влияние напряжений и деформаций, которые балка испытывает на левом пролете, сказываются и на правом пролете. Если в месте промежуточной опоры врезать шарнир в тело балки, то в результате система станет статически определимой - из одной балки мы получим две независимые друг от друга балки, каждая из которых будет статически определимой. Следует отметить, что неразрезные балки являются менее материалоемкими по сравнению с разрезными, так как более рационально распределяют изгибающие моменты по своей длине. В связи с этим неразрезные балки получили широкое применение в строительстве и машиностроении. Однако, неразрезные балки, будучи статически неопределимыми, требуют специальной методики расчета, включающей в себя использование деформаций системы.
Решение. В сечении А балка имеет жесткую опору, исключающую перемещение и поворот сечения. Такая опора соответствует наличию трех связей. На правом конце балка опирается свободно и имеет одну связь. Таким образом, балка имеет четыре связи при трех степенях свободы. Степень статической неопределимости балки равна единице. Изобразим балку и расставим “характерные” сечения: на левом конце, посредине и на правом конце (рис. 8.15, а). Оборвем одну связь в сечении В и действие связи заменим реакцией Х1 (рис. 8.15, б). Величина этой реакции неизвестна, но она должна быть такой, чтобы вертикальное перемещение сечения В было равно нулю. В этом условии будет заключаться эквивалентность исходной системы (рис. 8.15, а) и статически определимой системе, изображенной на рис. 8.15, б. Чтобы описать условие эквивалентности двух систем, воспользуемся принципом независимости сил, сначала изобразим балку, нагрузив ее только внешней нагрузкой (рис. 8.15, в). Перемещение сечения В, вызванное внешней нагрузкой, обозначим D1р. Далее изобразим балку, нагруженную только сосредоточенной силой Х1. Перемещение сечения В, вызванное этой нагрузкой, обозначим D11. Сумма этих перемещений должна равняться нулю, так как в исходной системе сечение В в вертикальном направлении не перемещается:
D11 + D1р = 0 (8.5)
Уравнение (8.5) удобно записывать в канонической форме:
d11·Х1 + D1р = 0 (8.6)
где d11·Х1 = D11. Здесь d11 - перемещение, вызванное силой, равной единице, приложенной в сечении В (рис. 8.15, е).
Неизвестную реакцию Х1 можно определить из уравнения (8.6), если предварительно найти перемещение D1р, которое назовем грузовым, и перемещение d11, которое назовем единичным. Чтобы определить грузовое перемещение D1р, построим грузовую эпюру изгибающих моментов (рис. 8.15, д), единичную эпюру (рис. 8.15, ж) и перемножим их, воспользовавшись формулой Мора-Симпсона:
В рассматриваемом примере:
Единичное перемещение d11 найдем, умножив единичную эпюру (рис. 8.15, ж) саму на себя. Для рассматриваемого примера
Подставляя найденные значения для D1р и d11 в уравнение (8.6) и решая его относительно Х1, найдем:
Суммарные изгибающие моменты в “характерных” сечениях балки найдем из выражения:
где n - число “лишних” неизвестных или степень статической неопределимости системы; i - номер “характерного” сечения. Для рассматриваемой балки:
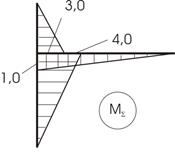
Откладываем найденные значения от базисной линии и строим эпюру суммарных изгибающих моментов (рис. 8.15, з). Для построения эпюры поперечных сил вырежем часть балки, расположенную между сечениями №1 и №3, приложим все действующие на вырезанный участок силы (рис. 8.16) и составим два уравнения равновесия, из которых найдем значения поперечной силы в “характерных” сечениях, расположенных на границах вырезанного участка:
Рис. 8.16
Учитывая, что
Особенно обстоятельно они разработаны для рам с прямолинейными стержнями постоянного сечения. Жесткость E I = const при этом выносится за знак интеграла, а под интегралом остается произведение двух функций: Mi и Mk, одна из которых, как правило, или обе являются линейными функциями. Операция интегрирования здесь часто называется перемножением эпюр и ее символически изображают следующим образом:
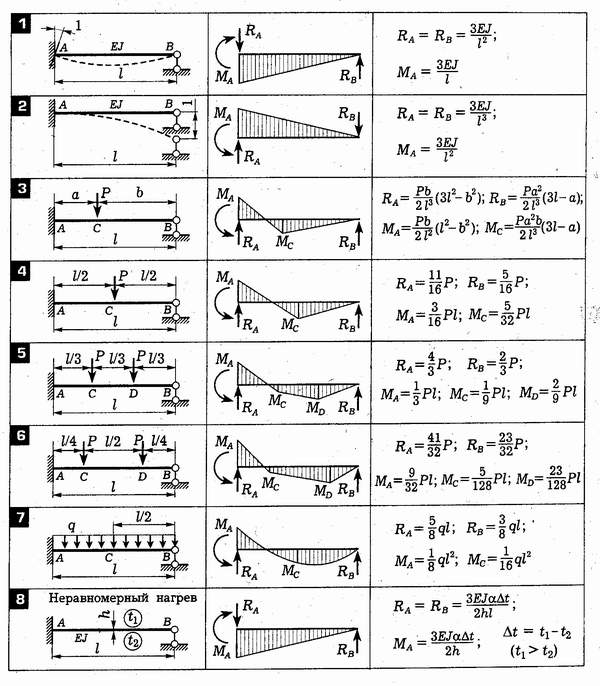
здесь знак Применение готовых формул показано в таблице 1. Сами эти формулы без труда определяются элементарными методами. Эта таблица является весьма универсальной, так как она пригодна для определения перемещений по двум любым прямолинейным эпюрам, а также криволинейной с прямолинейной. Если любая из фигур, приведенных в табл. 1, перемножается с треугольником, то это перемножение сводится к трапеции, одна из ординат которых равна 0. При перемножении на прямоугольник нужно учесть, что М a = Мb. При помощи расчленения эпюр на части можно добиться того, чтобы при перемножении участвовали эпюры простой структуры, приведенные в таблице 1.
Таблица 1
Например, пусть нужно перемножить эпюры, приведенные на рис. 32. Каждую из эпюр можно представить в виде суммы: в первом случае, в виде двух треугольных и параболической; во втором -в виде двух треугольных.
Рис. 32 Рис. 33 Итак,
Тогда
А далее следует воспользоваться формулой для вычисления интегралов Довольно удобным способом перемножения эпюр является способ Верещагина. Этот способ применим в случае когда из двух перемножаемых эпюр одна как минимум является прямолинейной. Если одна из эпюр является криволинейной вычисляется площадь
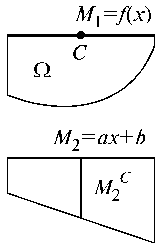
Предположим M 1 = f (x); M 2 = a x + b, тогда
но величина
Известно, что величина В случае двух криволинейных эпюр способ Верещагина неприменим. Надо пользоваться интегралом Мора. Способ Верещагина применим также в тех случаях, когда одна из эпюр не криволинейная, а ломаная. В таблице 2 приведены формулы для определения площади В случае, когда имеются эпюры общего вида (например, обе эпюры криволинейные, либо трапеции, рис.33, разбиение уже на два равных интервала дает согласно формуле Симпсона точное выражение интеграла:
где индексы А и С относятся к сечениям расположенным на концевых сечениях интервала длиной l, а индекс В к серединному сечению того же интервала. В тех случаях, когда функции M 1 и M 2 в рассматриваемом интервале длиной l, являются линейными и известны их значения в концевых сечениях интервала, то формулу перемножения M 1 и M 2 можно преобразовать в следующем виде:
Итак, после составления и решения канонической системы уравнений метода сил (7.4) мы получаем значения X 1, X 2, X 3,..., Xn, т.е. значения усилий в лишних связях. Затем строим для основной системы эпюры изгибающих моментов от каждого из найденных усилий. Для этого могут быть использованы построенные ранее единичные эпюры, все ординаты которых необходимо теперь умножить на найденные значения соответствующих неизвестных. Сложив по характерным сечениям (на протяжении всей рассчитываемой конструкции) ординаты эпюр от действия всех сил Xi с ординатами грузовой эпюры, получим окончательную (суммарную) эпюру изгибающих моментов в заданной статически неопределимой системе.
Таблица 2
Пример 1. Требуется раскрыть статическую неопределимость балки и построить эпюры изгибающих моментов и поперечных сил (рис.34, а). Решение. В сечении А балка имеет жесткую опору, исключающую перемещение и поворот сечения. Такая опора соответствует наличию трех связей. На правом конце балка опирается свободно и имеет одну связь. Таким образом, балка имеет четыре связи при трех степенях свободы. Степень статической неопределимости балки равна единице. Изобразим балку и расставим “характерные” сечения: на левом конце, посредине и на правом конце (рис.34, а). Оборвем одну связь в сечении В и действие связи заменим реакцией
Уравнение (19) удобно записывать в канонической форме:
где
Рис.34
Неизвестную реакцию Чтобы определить грузовое перемещение
В рассматриваемом примере:
Единичное перемещение Для рассматриваемого примера
Подставляя найденные значения для
Суммарные изгибающие моменты в “характерных” сечениях балки найдем из выражения:
где n - число “лишних” неизвестных или степень статической неопределимости системы; i - номер “характерного” сечения. Для рассматриваемой балки:
Откладываем найденные значения от базисной линии и строим эпюру суммарных изгибающих моментов (рис.34, з). Для построения эпюры поперечных сил вырежем часть балки, расположенную между сечениями №1 и №3, приложим все действующие на вырезанный участок силы (рис.35) и составим два уравнения равновесия, из которых найдем значения поперечной силы в “характерных” сечениях, расположенных на границах вырезанного участка:
Рис.35
Учитывая, что
Пример 2. Для балки (рис. 36, а) определим внутренние усилия.
Рис.36
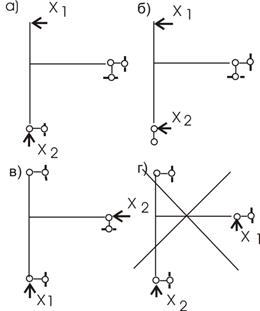
Решение. 1) Рассчитаем степень статической неопределимости n =5-3=2. Два раза статически неопределимая балка. Основные системы метода сил представлены на рисунке 36, б,в. Для расчета примем вариант 36, в. 2) Запишем систему канонических уравнений:
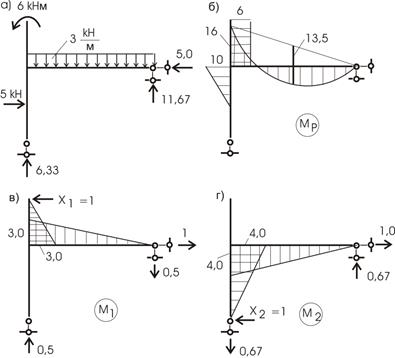
3) Вычисляем коэффициенты Эпюры от единичных загружений представлены на рисунке 37, б,в и от внешней нагрузки - на рисунке 37, г.
Рис.37
Решение системы:
дает По полученным значениям строим и Проверки. а) Статическая проверка. Значения моментов на опорах (рис. 38, в) одинаковы и равновесие обеспечивается. Проверка удовлетворяется. б) Кинематическая проверка.
Рис.38
Перемножим
Проверка удовлетворяется. Эпюра
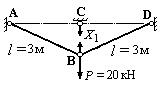
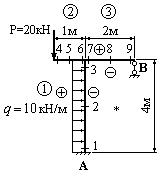
Пример 3. Определить усилия (в кН) в стержнях фермы, изображенной на рис.39.
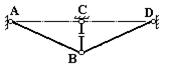
Рис.39 Решение. 1. Определяем степень статической неопределимости: n=3-2=1. 2. Выбираем основную систему (рис.40).Основная система получается из заданной путем рассечения одного из стержней, например, стержня ВС.
Рис.40. Основная система
3. Изображаем эквивалентную систему (рис.41).
Рис.41. Эквивалентная система
Каноническое уравнение метода сил имеет вид:
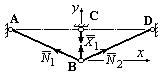
Физический смысл этого уравнения состоит в том, что взаимное перемещение сечений, которые получились при рассечении стержня ВС, равно нулю. 4. Изображаем грузовое состояние системы (рис.42) и определяем усилия в стержнях фермы АВ и ВD.
Рис.42. Грузовое состояние системы
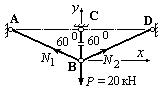
Составляем уравнения равновесия сил на оси x и y:
откуда находим:
5. Изображаем единичное состояние системы (рис.43) и находим единичные усилия в стержнях фермы:
Рис.43. Единичное состояние системы
Составляем уравнения равновесия на оси x и y:
откуда находим:
6. Определяем грузовое
Из канонического уравнения (23) находим “лишнюю” неизвестную
Усилия в стержнях
Подставляя в формулу (24) значения “лишней” неизвестной, грузовых и единичных изгибающих моментов, получаем:
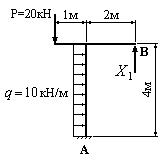
Пример 4. Определить реакцию опоры В рамы, изображенной на рис.44.
Рис.44
Следует отметить, что в заданной постановке можно избежать построения суммарных эпюр изгибающих моментов и поперечных сил для определения реакции опоры В. Для этого нужно выбрать таким образом основную систему, чтобы связь в опоре В оказалась “лишней”. Тогда “лишняя” неизвестная, заменяющая действие “лишней” связи, и будет искомой реакцией. Решение. 1. Разбиваем раму на участки, выбираем точку наблюдения, вводим положительные и отрицательные стороны и проставляем “характерные” сечения. 2. Определяем степень статической неопределимости: n=4-3=1. 3. Выбираем основную систему. Так как нас интересует реакция опоры В, принимаем в качестве “лишней” неизвестной
Рис.45. Основная система
4. Изображаем эквивалентную систему (рис.46).
Рис.46. Эквивалентная система
Каноническое уравнение метода сил имеет вид:
Физический смысл этого уравнения – равенство нулю перемещений в направлении “лишней” неизвестной 5. Изображаем грузовое состояние системы (рис.47, а) и строим грузовую эпюру изгибающих моментов
Рис.47
6. Изображаем единичное состояние системы (рис.48, а) и строим единичную эпюру изгибающих моментов
Рис.48
7. Перемножая грузовую эпюру
8. Перемножая единичную
Подставляя (26) и (27) в уравнение (25) и решая его относительно
Полученная значение для “лишней” неизвестной
Пример 5. Для заданной рамы (рис.49) требуется построить эпюры M, Q, N.
Рис.49
Решение. 1. Определяем степень статической неопределимости n =5-3=2 Для получения основной системы нужно отбросить 2 избыточные связи. 2. Выбираем основную систему. Варианты основной системы приведены на рисунке 50, а,б,в,г. Для расчета возьмем вариант 2 (выбор произвольный). 3. Запишем канонические уравнения для решения:
Рис.50
Для подсчета коэффициентов и свободных членов уравнений построим эпюры от единичных сил и внешней нагрузки (рис. 51, а,б,в,г).
Рис.51
Вычисление основных параметров для построения эп. М от внешней нагрузки:
То же для построения М1.
И для построения М2.
4. Вычисляем коэффициенты при x i по правилу Верещагина:
Вычисляем грузовые слагаемые:
Перед решением системы уравнений производим проверку правильности вычислений коэффициентов: а) построчная проверка
где
Равенство удовлетворяется.
Рис.52
б) суммарная проверка. Сумма всех коэффициентов = т.е.
т.е. 32,33=32,33. Условие удовлетворяется. в) проверка грузовых слагаемых
-8=-8. Условие удовлетворяется. 5. Решение системы производим по методу Гаусса
Для этого разделим первое уравнение на 27, а второе – на 24. Получим:
Складываем оба уравнения:
Отсюда находим:
Подставляем х 2 в любое уравнение системы:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

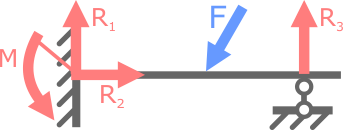 В качестве примера рассмотрим следующий случай:
В качестве примера рассмотрим следующий случай: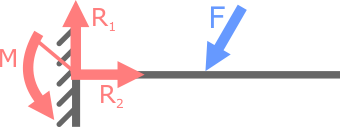


 (8.7)
(8.7)
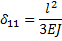

 (8.8)
(8.8)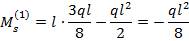
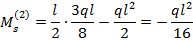
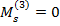
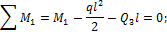
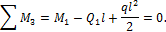

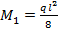 (знак момента учтен выбором его направления), из первого уравнения находим:
(знак момента учтен выбором его направления), из первого уравнения находим: 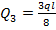 . Из второго уравнения находим
. Из второго уравнения находим 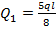 . По найденным значениям строим суммарную эпюру поперечной силы (рис. 8.15, и).
. По найденным значениям строим суммарную эпюру поперечной силы (рис. 8.15, и).
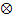 означает умножение в смысле формулы Мора.
означает умножение в смысле формулы Мора.







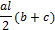
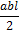
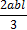
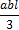

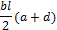
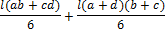
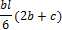


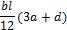
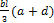

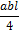
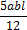

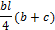
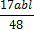

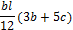
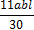

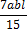

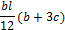
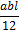
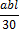


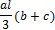
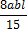
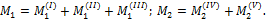
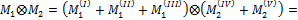
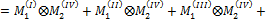
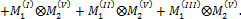
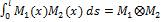 , приведенных в таблице 1.
, приведенных в таблице 1. криволинейной эпюры, которая умножается на ординату под ее центром тяжести, взятую в прямолинейной эпюре
криволинейной эпюры, которая умножается на ординату под ее центром тяжести, взятую в прямолинейной эпюре 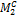 (рис.33).
(рис.33).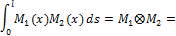
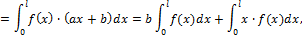
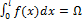 представляет собой площадь криволинейной эпюры, а величина
представляет собой площадь криволинейной эпюры, а величина  - статический момент площади этой эпюры относительно левого конца стержня. Следовательно,
- статический момент площади этой эпюры относительно левого конца стержня. Следовательно,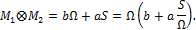
 представляет собой ординату центра тяжести криволинейной эпюры, а
представляет собой ординату центра тяжести криволинейной эпюры, а  - значение M 2 при
- значение M 2 при 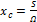 .
.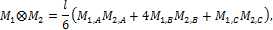
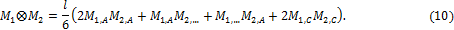
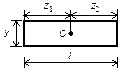

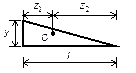
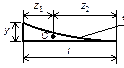
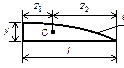
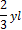

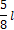
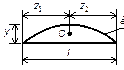
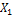 (рис.34, б). Величина этой реакции неизвестна, но она должна быть такой, чтобы вертикальное перемещение сечения В было равно нулю. В этом условии будет заключаться эквивалентность исходной системы (рис.34, а) и статически определимой системе, изображенной на рис.34, б. Чтобы описать условие эквивалентности двух систем, воспользуемся принципом независимости сил, сначала изобразим балку, нагрузив ее только внешней нагрузкой (рис.34, в). Перемещение сечения В, вызванное внешней нагрузкой, обозначим
(рис.34, б). Величина этой реакции неизвестна, но она должна быть такой, чтобы вертикальное перемещение сечения В было равно нулю. В этом условии будет заключаться эквивалентность исходной системы (рис.34, а) и статически определимой системе, изображенной на рис.34, б. Чтобы описать условие эквивалентности двух систем, воспользуемся принципом независимости сил, сначала изобразим балку, нагрузив ее только внешней нагрузкой (рис.34, в). Перемещение сечения В, вызванное внешней нагрузкой, обозначим 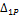 . Далее изобразим балку, нагруженную только сосредоточенной силой
. Далее изобразим балку, нагруженную только сосредоточенной силой 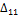 . Сумма этих перемещений должна равняться нулю, так как в исходной системе сечение В в вертикальном направлении не перемещается:
. Сумма этих перемещений должна равняться нулю, так как в исходной системе сечение В в вертикальном направлении не перемещается:

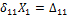 . Здесь
. Здесь 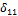 - перемещение, вызванное силой, равной единице, приложенной в сечении В (рис.34, е).
- перемещение, вызванное силой, равной единице, приложенной в сечении В (рис.34, е).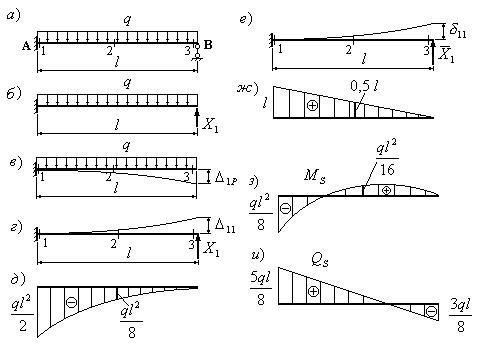
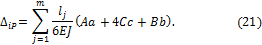

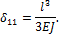
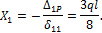


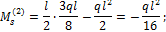
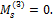
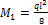 (знак момента учтен выбором его направления), из первого уравнения находим:
(знак момента учтен выбором его направления), из первого уравнения находим:  . Из второго уравнения находим
. Из второго уравнения находим 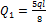 . По найденным значениям строим суммарную эпюру поперечной силы (рис.34, и).
. По найденным значениям строим суммарную эпюру поперечной силы (рис.34, и).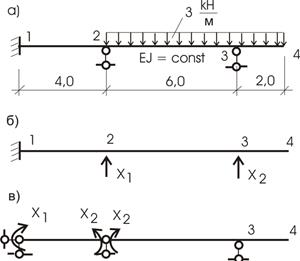
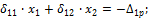
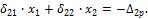
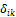 и
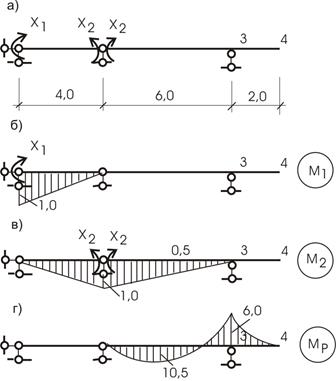
и  .
.

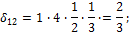
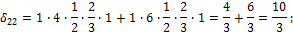
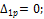
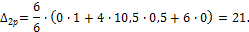
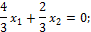


 и
и 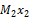 (рис. 38, а,б)
(рис. 38, а,б)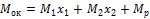 (рис. 38, в).
(рис. 38, в).
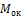 с
с 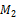 . Проверим, будет ли взаимный угол поворота сечений балки на опоре 2 равен нулю?
. Проверим, будет ли взаимный угол поворота сечений балки на опоре 2 равен нулю?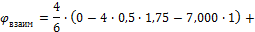

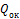 строится по эпюре
строится по эпюре 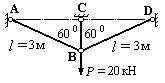
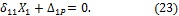
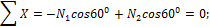
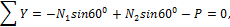
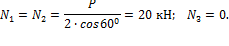
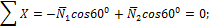
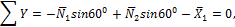
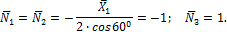
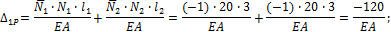
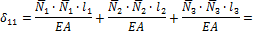
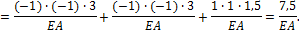

 и
и 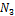 найдем из формулы:
найдем из формулы: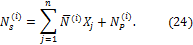


 , вызванное самой “лишней” неизвестной и внешней нагрузкой.
, вызванное самой “лишней” неизвестной и внешней нагрузкой. (рис.47, б).
(рис.47, б).
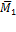 (рис.48, б).
(рис.48, б).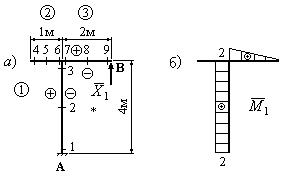
 и единичную эпюру
и единичную эпюру 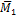 изгибающих моментов по формуле Мора-Симпсона, находим грузовое перемещение
изгибающих моментов по формуле Мора-Симпсона, находим грузовое перемещение 

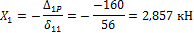
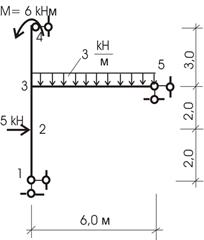
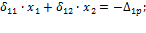

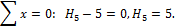
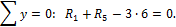
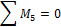
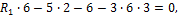
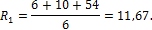
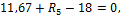

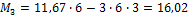

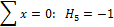
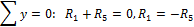


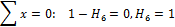
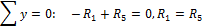
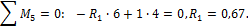
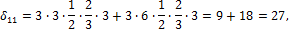
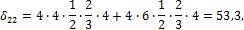
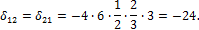
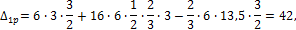
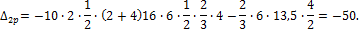
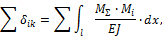
 - суммарная эпюра моментов от единичных сил (рис. 52) и для первой строки
- суммарная эпюра моментов от единичных сил (рис. 52) и для первой строки