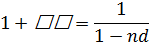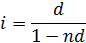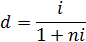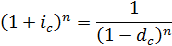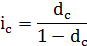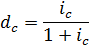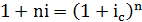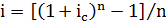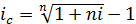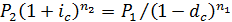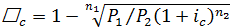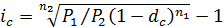Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 6. Эквивалентные и эффективные процентные ставки.Содержание книги
Поиск на нашем сайте
Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условий дает одинаковые финансовые результаты. Они применяются в случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок. Для нахождения эквивалентных процентных ставок используют уравнения эквивалентности, принцип составления которых заключается в следующем. Выбирается величина, которую можно рассчитать при использовании различных процентных ставок (обычно это наращенная сумма S). На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида. Приравнивая эти формулы попарно, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками. Например, задана исходная сумма Р, годовая процентная ставка (номинальная) j, количество начислений сложных процентов m. Этому набору исходных величин в рамках одного года соответствует вполне определенное значение наращенной суммы S. Требуется найти такую годовую ставку В рамках одного года при многократном начислении процентов:
При однократном начислении процентов:
В левой части каждого из уравнений – одна и та же величина, а потому, приравнивая правые части уравнений, находим формулу взаимосвязи процентных ставок.
Полученная годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов и показывает реальную доходность финансовой операции. Она также позволяет сравнивать процентные ставки, когда используются различные интервалы начисления. Из полученной формулы следует, что эффективная ставка
Пример 1. Предприниматель может получить ссуду на следующих условиях: 1. Ежемесячное начисление процентов из расчета 26% годовых. 2. Полугодовое начисление процентов из расчета 27% годовых. Какой вариант предпочтительней? Решение. Относительные расходы предпринимателя по обслуживанию ссуды могут быть определены с помощью расчета эффективной годовой процентной ставки. Чем она выше, тем больше уровень расходов. Вариант 1.
Вариант 2.
Т.о., вариант 2 является более предпочтительным для предпринимателя. При этом принятие решения не зависит от величины кредита. Пример 2. Каков размер эффективной ставки, если номинальная ставка равна 25% при помесячном начислении процентов?
Т.о., для участвующих в сделке сторон безразлично применять 25% при помесячном начислении процентов или эффективную (годовую) ставку 28,0732%. Из данной формулы можно выразить и номинальную ставку процентов:
Зависимость между простой ссудной и простой учетной ставками будет выражаться:
Зависимость между сложной ссудной и сложной учетной ставками будет выражаться:
Зависимость между сложной ссудной и простой ссудной ставками будет выражаться:
Можно определить также процентную ставку, эквивалентную данной, когда начальные условия полностью или частично не совпадают. Данная ситуация может возникнуть, например, если есть возможность выбора между различными коммерческими предложениями.
Пример. Какова должна быть сложная ставка dc, чтобы сумма Р1, вложенная под эту ставку на n1 лет, достигла той же величины, что и сумма Р2, вложенная под сложную ставку ссудного процента ic на n2 лет?
Составим уравнение эквивалентности:
Отсюда:
Уравнение можно решить и относительно сложной ссудной ставки:
|
|||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.140.29 (0.009 с.) |

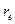 , которая обеспечила бы точно такое же наращение, как и исходная схема, но при однократном начислении процентов, т.е. при m=1.
, которая обеспечила бы точно такое же наращение, как и исходная схема, но при однократном начислении процентов, т.е. при m=1.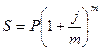

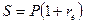
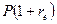 =
= 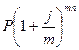
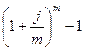
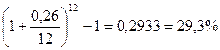
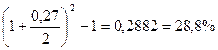
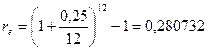
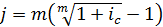 .
.