Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чем отличается «гармоника» от «гармонии»?Содержание книги Поиск на нашем сайте
Как мы понимаем красоту? Обязательно прочитать книгу мемуаров Валерия Александровича Гаврилина “Музыка. И не только о ней” о восприятии музыки, о Шостаковиче и о Соловьеве-Седом, об авторах и исполнителях, о вокальном творчестве вообще. Ведущий радиопередачи Борис Эйфман ссылался еще на книгу Белинского (не помню имени автора) “Записки старого сплетника”. В.А.Гаврилин был учеником Г.Свиридова. ПЛАН:
1. Предисловие. 2. Чем отличается «гармоника» от «гармонии»? 3. Вопросы по ранжиру. 4. Немного из истории. 5. Соотношения форм. 6. Соотношения звуков. 7. Соотношения цветов. 8. В чем различие и сходство между ушами и глазами? 9. Почему же “на вкус и цвет товарища нет”? 10. К вопросу о воспитании вкуса у детей и взрослых. 11. О возможностях компьютеризации оценки красоты. 12. О предназначении и взаимодействии творца и публики. 13. Возможности гармонического “роста”. 14. О красоте художественного костюма. 15. Доступен ли человеческому восприятию хаос?
Предисловие. Эта статья была написана потому, что возникло желание поделиться. А именно, - самими наблюдениями за окружающим нас миром, который не скрыт ни от кого. Почему нам нравятся или нет некоторые объекты изобразительного искусства, музыки, архитектурного, технического дизайна и так далее? Почему пословица: “на вкус и цвет товарища нет”, - многим кажется аксиомой, так ничего и не объясняя? Какую работу проводит наш мозг, когда мы подсознательно задаем себе вопрос: А красиво это… или нет?
Эти вопросы занимали автора очень долго, потому что работать, ему приходилось со сложными спектрами звучания современной электрогитары, пропущенной через электронный эффект “дисторшн”.
Этот эффект “обогащает” звучащий спектр (тембр) музыкального инструмента различными гармониками (призвуками). Что такое гармоники вы можете прочитать чуть ниже. Эффект дает “ревущий”, “стонущий” или же “визжащий” звук гитары. В общем, эмоционально наполненный и тембрально управляемый спектр, что в свою очередь раскрывает дополнительные возможности перед исполнителем.
Эти гармоники могут находиться в кратных или не кратных соотношениях (по частоте) с основной звучащей нотой или же в еще более сложных соотношениях со спектром нескольких нот (аккорда) и гармоник, образованных еще и от них, пришедших на вход электронного эффекта.
Отсюда следует, что получение на выходе электронного устройства относительно красивого гармонического спектра при таком богатстве гармонических составляющих, - задача очень «непростая». К тому же, происходит это все - в динамике, т. е. при изменяющихся амплитудах (громкостях) гармоник выходного спектра электрогитары, что неизбежно происходит при затихании струн и в зависимости от многих критериев качества звучания инструмента.
Наконец-то, лет через двадцать чуть ли не каждодневного “задавания самому себе” вопроса: ” красиво - некрасиво ” и нескончаемых споров со своими клиентами-музыкантами, - людьми, достаточно тонко чувствующими красоту, начало складываться понимание природы красоты звучащих спектров, а вскоре пришла и уверенность в знании на уровне «знаю» (или NOUS).
Ответ, который пришел в результате этих исследований, настолько прост что, сразу даже и в голове не укладывался, - дело в соотношениях!
На самом деле! Давайте зададимся вопросом: “Как наш мозг может сравнивать объекты окружающего нас мира, не имея изначально заложенной точки отсчета?” Как известно, все происходящие события вокруг нас реализуются в трех воспринимаемых нашим мозгом измерениях и во времени. С “измерениями” совсем плохо. У всех народов системы разные, - и десятикратные, и двенадцатикратные и другие. Действительно: мы можем “на глазок прикинуть”, что один объект больше или меньше другого в два раза, в три раза… реже можем сказать, что этот объект составляет, например, три или две пятых другого, и совсем немногие могут определить, что соотношение - пять к семи. Сравнительно легко мы можем определять четные соотношения.
В современном мире уже и шагу не ступить без дизайна. Он уже стал “наукой”. Почему в кавычках? Потому, что, я вас уверяю, эта “наука” занимается тем же самым, чем занимается мозг каждого живущего человека, только с гораздо большей эффективностью. И человек, с достаточно развитым гармоническим восприятием - вкусом, может оценить красоту гораздо точнее и тоньше, чем некий дипломированный дизайнер.
Беда в том, что он не может объяснить себе и окружающим этого знания. Я попробую!
Например: каждому начинающему дизайнеру должен быть известен факт, что, если соотношения размеров, площадей или объемов расходятся с простыми целочисленными соотношениями больше, чем на три процента, то это уже “некрасиво”, - у простого человека “глаз чует” расхождение. Теперь ответьте, - многие из вас знакомы с этим постулатом дизайна?
Более того, - соотношения могут быть не только линейными (назовем их соотношениями первого порядка). Они могут быть, например, квадратичными, или привязанными к экспоненте, или к другим функциям (назовем их соотношениями второго порядка). Наконец, они могут быть полифункциональными, то есть описываться с помощью интегрирования – дифференцирования (назовем их соотношениями третьего порядка).
На самом же деле наш мозг постоянно на подсознательном уровне сравнивает и подсчитывает эти соотношения… и гораздо более тонкие и многоплановые – т.е. все!
Вы можете возразить, что дизайнеры оперируют не только размерами и формами, но еще и цветами, и даже звуками.
С этим, как раз, все намного проще, чем с размерами. Дело в том, что звук – это периодический процесс, в котором колебания давления воздуха происходят равномерно с какой-нибудь частотой, причем равномерность обусловлена резонансом источника звука, а частота – это и есть высота тона. Чем чаще – тем выше тон.
С цветом - то же самое, только глаз воспринимает разную частоту колебаний электромагнитного излучения, как разные цвета. При понижении частоты колебаний, - восприятие смещается в красную сторону, при повышении – в фиолетовую сторону.
Так вот наш мозг оперирует соотношениями этих частот, т. е. сколько раз, например, изменилось давление воздуха (в случае со звуком) за определенный период времени, образуя одну ноту, и сколько, образуя другую.
Вопросы по ранжиру. Давайте попробуем разобраться, какие вопросы нам надо затронуть, чтобы попытаться разобраться в этой загадке.
Во-первых, нас интересует, чем обусловлена «заинтересованность» человеческого мозга в притоке, накоплении и упорядочивании новой информации. Тут, очевидно, необходима помощь психологов и философов.
Во-вторых, нас интересует физиология процессов записи и считывания информации мозгом. Здесь потребуется помощь нейрофизиологов.
В-третьих, нас интересует сама физика процессов, воспринимаемых человеческим мозгом посредством «датчиков», - будем рассматривать пока только глаза и уши. Тут потребуется помощь физиков: спектрологов и акустиков.
Ну и, в-четвертых: не пытался ли кто-нибудь и прежде разобраться в этом, - необходима помощь историков.
Конечно же, у автора этих строк не нашлось в жизни столько ресурсов, чтобы привлечь всех этих специалистов, провести исследования и научно доказать свою догадку. Более или менее подробно мне удалось разобраться только со звуком, поскольку сам я бывший музыкант и звукорежиссер (поэтому и в дальнейшем буду развивать свою теорию в основном на просторах акустики).
Тем не менее, когда мне пришлось всерьез заняться интерьерным дизайном, я с радостью обнаружил, что принципы восприятия красивого в сочетаниях размеров, в цветовых сочетаниях абсолютно аналогичны музыкальным.
Именно это главное «открытие», в основном, и подтолкнуло меня к написанию статьи!
Немного из истории.
Конечно же, я не первый, кто задался этими вопросами. Еще древние греки всерьез интересовались соотношениями, а Пифагор, вообще, считал, что изучение соотношений – ключ к пониманию всего сущего. Предлагаю всем, кому интересно, перечитать философов прошлого. Они и теперь также актуальны, как и в свое древнее время.
Что же такое форма?
Во все времена, начиная, наверное, с пещерного периода, люди пытались создать что-либо красивое. Попробуем разобраться, что именно в самом начале развития гармонического восприятия могло быть правильно соотнесенным? Конечно, это размеры!
Наверное, первые образчики оружия, посуды, мебели давали чувство красоты их творцам, только если имели простые целочисленные соотношения размеров своих элементов, к тому же видные и понятные другим особям.
Затем стали создаваться первые искусственные жилища. К этому времени, я думаю, у людей уже были вполне определенные понятия о красоте. Так появились зачатки архитектуры. Ну и поехали, - от египетских пирамид до греческого Парфенона. Через романский и готический стили, барокко до санкт-петербургских дворцов. От первого шалаша до современных монстров из стекла, металла и бетона, - человек пытался все сделать красиво.
Я считаю, что начинать изучение архитектуры теперь надо в обратном хронологическом порядке, - на этих примерах проще показать соотношения размеров, площадей, углов, радиусов. А вот в европейских (в том числе и питерских) дворцах присутствуют гармонии и низшего порядка, и также гармонии среднего и высшего порядков, которые почувствовать и воспринять сразу очень не просто.
Или взять, к примеру, технический дизайн. Те, кто постарше помнят: какими обтекаемыми и простыми были обводы ракет на иллюстрациях к фантастическим романам шестидесятых годов. А какими стали теперь космические монстры в современных компьютерных играх, которых уже практически никто, кроме специалистов, красивыми и не назовет? На самом-то деле они действительно очень красивы, но дело совсем в другом. В первом случае рисунки делали художники-романтики, желающие вложить всем и каждому понятные элементы красоты, то есть рисунки содержали только легко просчитываемые нашим подсознанием сочетания углов, радиусов и т.д. Во втором же случае модели разрабатывались современными компьютерами, и уж кого-кого, а их-то никак не заподозришь в создании случайного хаотичного проекта, - все математически выверено. Просто дело в том, что эти сочетания форм, размеров, площадей, радиусов уже настолько развиты, что стали попросту недоступны нашему гармоническому восприятию, - программисты перестарались.
За этим эффектом, кстати, тщательно следят современные автодизайнеры, - чтобы сочетания обводов и форм современного автомобиля лежали в диапазоне гармонического восприятия массового потребителя автопрома, - тот же шоу-бизнес. Что же такое звук?
Из курса физики нам известно, что звук – это периодическое изменение давления проводящей волны среды. Средой обычно является воздух, но это может быть и вода и любые другие среды. Сейчас мы рассматриваем воздух, поскольку, обычно, музыку под водой не слушаем. На наше счастье периодические процессы, образующие звуки, равномерны. Это значит, что временной интервал между соседними пиками звукового давления примерно одинаков на сравнительно большом промежутке времени, то есть соотношение количества этих одинаковых промежутков с пиками давления ко времени, в котором мы воспринимаем звук, большое.
Например: нота “ля” первой октавы при звучании образует 440 равномерных колебаний звукового давления за одну секунду. Именно поэтому нашему мозгу легко выделять основной тон (тонику) в звуке. А представьте себе: как, например, определить тон в звуке сирены, где он постоянно меняется в диапазоне трех октав (частота колебаний изменяется в четыре раза) с периодом в несколько секунд? Но ведь любой природный звук, как нам кажется, может менять тон гораздо быстрее. Тогда временные промежутки между пиками станут заметно не одинаковыми, звуковой процесс перестанет быть периодическим, и нашему мозгу станет на несколько порядков сложнее оценивать соотношение временных интервалов между пиками давления воздуха, то есть невозможно для “среднего ума”. Это описан, практически, звуковой Хаос.
На самом деле это не так, хотя Вы, конечно, можете возразить, что в природе много просто шумов. Отчасти вы правы, но дело в том, что практически любой шум представляет собой спектр, то есть большой набор различных гармоник (призвуков), в котором последние, в основном, постоянны по частоте колебаний во времени, - т.е. переодичны. Меняются же чаще всего только по амплитуде, образуя опять-таки вездесущие выбросы звукового давления, но уже следующего порядка. Таким образом, любой шум состоит из набора гармоник, - набора правильных чистых синусоид, резонанс, а значит и равномерность каждой из которых обеспечена своими причинами. Обычно это или резонансы источника звука, или, что еще чаще, резонансы какого-то искажающего фактора при отражении или прохождении звуковой энергии через какую-то среду.
Отсюда вытекает несколько вопросов:
Это вопросы к физикам, физиологам, но больше всего, я уверен, к философам!
С первым вопросом более-менее ясно, - это резонанс - стабильность физических свойств среды, в которой происходит возбуждение и протекание звука. То есть среды самого источника и различных сред, проводящих и отражающих звуковую энергию.
В случае со светом, - стабильность атомного строения.
Именно эта стабильность и “отвечает” за то, что следующая волна будет точно такая же, как и первая, т. е. за равномерность периодического процесса.
Отсюда же предположение: “Очевидно, в окружающем нас мире существует еще множество других гармонических процессов, которые мы просто не видим, не слышим и наш мозг не способен их просчитать”.
Например: человеческий свист через губы представляет собой синусоиду. Это и есть моно- звук или гармоника, а не спектр, и он дает ощущение «гладкости» и «чистоты».
Давайте, «для простоты», попробуем разобраться с шумом на примере звучания оркестра.
Там звучит много инструментов одновременно, то есть гармоник (не будем пока для простоты рассматривать тембры, т.е. спектры звучания разных инструментов, а примем каждый из них за простейшую синусоиду). Что у нас при этом происходит в физической воздушной среде. Каждый инструмент издает свою ноту. Мгновенные перепады давления звуковых волн при смешении складываются в фазах и вычитаются в противофазах. Представим себе графики сложения этих звуков. При совпадении в фазах возникают пики давления, а при совпадении в противофазах - провалы его же. И частота появления этих пиков называется интермодуляцией у акустиков и биениями у музыкантов. Из графиков видно, - эта частота ниже звучащих нот, и воспринимается как биения громкости. Причем чем меньше расхождение в частоте у двух нот, тем частота биений ниже. Кто настраивал, хоть раз, гитару поймет, о чем я говорю. По сути дела эта частота, при условии, что ее источниками являются очень высокие ноты и сильно расстроены, становится слышимой (звуковой). А хуже всего, что звучание большинства музыкальных инструментов не является моно-гармоническим (за исключением, пожалуй, флейт), все они имеют свои тембры, то есть наборы своих гармоник-призвуков, частоты которых выше основных извлекаемых нот. При этом смешении тембров и образуется та самая слышимая интермодуляция, воспринимаемая нами как грязь (поскольку никакой мозг даже на подсознательном уровне не способен просчитать такую какофонию, образованную от такого количества плохо соотносящихся гармоник).
Теперь поговорим о хорошем: кто и как борется «за чистоту звука».
Прежде всего, наш мозг может разложить сумму приходящих на барабанную перепонку звуковых давлений на звучание отдельных музыкальных инструментов. Как это происходит? – вопрос очень интересный и до конца не изученный.
Далее:
Во-первых, звукорежиссеры на записях и на концертах пытаются минимизировать уровень слышимой интермодуляции (читай - грязи) всеми техническими средствами, это кроме основной своей обязанности максимального снижения влияния физических резонансов помещения, в котором проходит концерт или запись.
Во-вторых, дирижеры распределяют громкости звучания и акценты в группах инструментов и в звучании отдельных таким образом, чтобы достигнуть максимальной выразительности. А это как раз достижимо, при минимальной интермодуляции, то есть максимальной прозрачности звучания оркестра.
В-третьих, сами композиторы заботятся о достаточной насыщенности или же необходимой прозрачности структуры своего музыкального произведения в зависимости от поставленных художественных задач.
В-четвертых, каждый настоящий музыкант считает себя обязанным настроить свои инструмент так, чтобы при звучании в оркестре он не вносил «грязи», а только «красоту». А в групповом звучании с аналогичными инструментами быстро попадал в унисон - частотное и фазовое совпадение, сопровождаемое усилением звучащей группы.
В-пятых, производители музыкальных инструментов.
Например: принцип создания скрипки знаменитым Страдивари был основан на том, что каждая нота хроматического ряда (всех нот подряд по полутонам), которую будут извлекать на этом инструменте, должна находить резонирующий отклик в деке инструмента. То есть каждая дека строилась из дощечек, резонирующих каждая на свой полутон, и располагались они при склеивании в определенном порядке.
Почти на том же принципе построена знаменитая гитара Les Paul (фирмы Gibson) Гарри Мура. Она состоит из шестнадцати пород дерева. А нужно ему это было для того, чтобы при игре через дисторш и попадании звука в кольцо обратной связи с динамиком усилителя (т.н. «заводке»), в общем спектре звучания гармоник, образованных дисторшном, сильнее выделялся резонанс первой гармоники (основной звучащей ноты), что как раз и дает его фирменное «округлое» звучание.
Отдельного разговора заслуживает лаковое покрытие, с которым интенсивно экспериментировал тот же Амати, да и другие мастера того времени, и которое в немалой степени отвечает за тембровый состав звучащего спектра инструмента.
Или пример с созданием первых синтезаторов, разрабатываемых и производимых тогда, в основном, в Японии. Программируемых пресетов звучания тогда еще не было. И общую огибающую громкости, и гармонический состав нот, и динамику этих гармоник можно было задавать вручную. Но вот в чем особая заслуга этих разработчиков: кроме набора красивых, прозрачных и, в общем, «правильных» пользовательских тембров, они ввели в синтезатор анализатор гармонических соотношений для проверки вновь образованных вручную тембров. Этот анализатор как бы выставлял вам оценку: плохой звук, так себе или же хороший, таким образом, помогая вам в регулировке некоторых параметров звучания и в то же время отслеживая общую картину получившегося звука.
Ну и не будем забывать про само разделение звукового ряда одной октавы (частота меняется в два раза) с помощью логарифма на двенадцать полутонов, образуя прогрессию, да и всего слышимого нами звукового диапазона, который составляет десять с половиной октав (частоты от 16 Герц, то есть колебаний в секунду, до 20000 Герц).
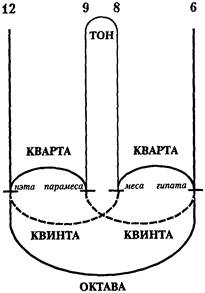
Вот, что об этом открытии Пифагора сообщает нам Ямвлих в своем труде «О Пифагоровой Жизни» (кому не интересно, - можно пропустить). ГЛАВА XXVI Однажды он пребывал в напряженном размышлении над проблемой, можно ли придумать для слуха какой-нибудь вспомогательный инструмент, надежный и не вводящий в заблуждение, каким для глаза является циркуль, отвес и, разумеется, диоптры, а для осязания – весы и изобретение мер. По счастливой случайности проходя мимо кузницы, Пифагор услышал, как на наковальне ковали железо и одновременные удары молотов издавали очень гармоничные звуки, кроме одного сочетания. Он различил в них октаву и созвучия, построенные на квинте и кварте, а интервал между квартой и квинтой он видел как не образующий гармонии сам по себе, но заполняющий расстояние между ними. Радуясь, как будто он получил эту идею от богов, он вбежал в кузницу и методом проб выяснил, что звучание зависит от тяжести молота, а не от силы удара, формы молота или изменения положения железа, которое ковали. Узнав точный вес молотов и установив, что их наклон при ударе одинаков, он удалился к себе домой. На один колышек, вбитый между углами стен (чтобы не внести в эксперимент никаких различных данных и чтобы вообще не было разницы между колышками), он повесил четыре струны из одного и того же материала, сплетенные из равного числа нитей, с одинаковой толщиной и одинаково скрученные. Он подвесил к ним разные грузы и сохранил равную их длину. Затем, ударяя поочередно по паре струн, он нашел созвучия, о которых говорилось выше, в разных сочетаниях струн. Он установил, что струна, к которой прикреплен самый большой груз, и струна, к которой прикреплен наименьший груз, образуют октаву. Так как к первой было подвешено 12 гирек, а ко второй – шесть, то он открыл, что октаве свойственно отношение 2:1, что подтверждало и весовое соотношение гирек. С другой стороны, он открыл, что между струной с самым большим весом и ближайшей к самой легкой, имевшей восемь гирек, был интервал в квинту и, следовательно, полуторное отношение, и в полуторном отношении находились и подвешенные к ним грузы. 104 Между струной с самым большим весом и следующей, которая была с большим грузом, чем другие, – к которой были подвешены девять гирек, – был интервал в кварту соответственно подвешенным грузам 105. Он выяснил, что эта струна (с девятью грузами) находится в отношении 3:4 к струне с самым большим грузом и что одновременно эта струна находится в полуторном отношении к струне с наименьшим весом, Поскольку девять именно так относится к шести 106. Равным образом струна, следующая за струной с наименьшим весом, к которой было прикреплено восемь гирек, образовывала со струной, имевшей шесть гирек, отношение 4:3, а со струной, которая имела 12 гирек, находилась в полуторном отношении. Следовательно, интервал между квинтой и квартой, на который квинта превосходит кварту, был установлен в отношении 9:8 107. Звукоряд в октаве раскрывался двояко, либо с сочетанием квинты с квартой, как трехчленная пропорция 12:8:6 108, либо, в обратном порядке, с сочетанием кварты с квинтой, как трехчленная пропорция 12:9:6. 109 Набив руку и изощрив слух на опытах с весами и открыв их пропорции, он искусно перенес общее крепление струн с вбитого на углу стены колышка на подставку под струны в лире, которую он назвал орудием натяжения струн, а натяжение струн в повороте колков в верхней части инструмента было аналогично подвешенным грузам. Благодаря этому эксперименту, словно с помощью точного инструмента, он распространил наконец свой опыт на различные инструменты: цимбалы, флейты, свирели, монохорды, тригон110 и подобные им и нашел, что во всех них арифметическое отношение было одинаково гармоничным. Он назвал звук, соответствующий числу 6, гипатой 111; звук, соответствующий числу 8 и находящийся в отношении 4:3 к гипате, – месой 112; звук, следующий за месой, выражающийся числом 9 и звучащий тоном выше, чем меса, и находящийся к ней в отношении 9:8, – парамесой 113, а звук, соответствующий числу 12, – нэтой 114. Заполнив интервалы соответственно диатоническому роду пропорциональными звуками, он подчинил таким образом октахорд 115 числовой гармонии, существующей в отношениях 2:1, 3:2, 4:3 и отличном от них отношении 9:8.
Таким образом он обнаружил в диатоническом роде необходимую и естественную прогрессию тонов от самого низкого звука к самому высокому. Начав с диатонического рода, он описал хроматический и энгармонический род, о чем мы расскажем, когда речь пойдет специально о музыке. Диатонический же род являет следующие ступени и такое естественное движение: полутон, тон, затем еще тон, и это есть кварта, соединение двух тонов и так называемого полутона. Затем, с прибавлением другого тона, вставленного в середину, образуется квинта, соединение трех тонов и полутона. Затем следуют полутон, тон и еще тон – другая кварта, то есть еще одно отношение 4:3. Поэтому в более древнем гептахорде116 каждый четвертый звук, начиная с самого низкого звука, образовывал созвучие кварты во всем звукоряде, причем полутон занимал поочередно первое, среднее и третье места тетрахорда. В пифагорейском октахорде, представлял ли он сочетание тетрахорда с пентахордом или два несовпадающих тетрахорда, отделенные друг от друга целым тоном, мелодическое движение начиналось от самого низкого звука, так что каждый пятый звук образовывал созвучие квинты, а полутон здесь последовательно занимал четыре места: первое, второе, третье и четвертое. Вот так, рассказывают, открыл он искусство музыки и, изложив систематически, передал его ученикам для всех самых прекрасных целей. 104. 12:8=3:2 (квинта). 105. 12:9=4:3 (кварта). 106. 9:6=3:2 (квинта). 107. 3/2:4/3 = 9/8 (один тон) – большая секунда. 108. 12:6 = 2:1 – октава, 12:8 = 3:2 – квинта, 8:6 = 4:3 – кварта. 109.12:9 = 4:3 – кварта, 9:6 = 3:2 – квинта. 110. Монохорд – однострунный инструмент для определения высоты тона. Тригон – инструмент треугольной формы, похожий на арфу. 111. Гипата – "крайняя" (струна), дававшая самый низкий тон. 112. Меса – "средняя" (струна). 113. Парамеса – "ближайшая к средней" (струна), то есть вторая из пяти струн лиры. 114. Нэта – "последняя" (струна). 115. Октахорд – образуется из двух тетрахордов, так что верхний тон нижнего тетрахорда совпадает с нижним тоном верхнего тетрахорда. 116. Гептахорд – "семиструнник". ______________________________________________________________________ От себя добавлю, что каждый начинающий бас-гитарист до сих пор начинает создавать гармонический фундамент (применительно к тонике каждого аккорда) именно по этим схемам: 12:8:12 – тоника - кварта (вниз) – тоника. 6:9:12 – тоника – квинта (вверх) – октава (верхняя тоника). К тому же в музыке есть понятие консонансов и диссонансов. В музыке ими определяются хорошо сочетающиеся пары (или группы) нот и плохо. К консонансам в пределах одной октавы относятся следующие интервалы: малая и большая терции (интервал, охватывающий 4 и 5 полутонов соответственно), кварта (6 полутонов), квинта (8 полутонов), малая и большая секста (9 и 10 полутонов соответственно), октава (интервал, охватывающий 13 полутонов, - один лишний полутон уже из следующей октавы).
К диссонансам относятся следующие интервалы: малая и большая секунды (2 и 3 полутона соответственно), тритон (7 полутонов), малая и большая септимы (11 и 12 полутонов соответственно).
Попробуем разобраться с физико-психологической точки зрения.
Во-первых: Частоты нот, составляющих консонансы, соотносятся по закону гармонического ряда. Например: октава – 1/2, квинта – 2/3, кварта – 3/4, и т.д.
Сплошная арифметика!
Во-вторых: Как мы уже знаем, при звучании двух (и более) нот одновременно в результате их простого сложения в воздухе образуются положительные и отрицательные пики звукового давления, - т.н. «биения» или, как говорят звукотехники - интермодуляция, частота которой ниже, но, тем не менее, это равномерный периодический процесс.
Естественно, что наш мозг не может отфильтровать эти амплитудные биения и пытается сравнить на подсознательном уровне эту частоту с частотами самих этих двух нот.
И вот что интересно. В случае консонансов частоты нот более или менее кратны частоте интермодуляции (биениям), то есть эти соотношения сравнительно легко просчитываемы нашим мозгом, а в случае диссонансов – нет.
Частота этих биений в соотношениях с двумя воспроизводимыми нотами высчитывается очень просто, например квинта: Ля – 2 части, Ми – 3 части, биения – 3ч - 2ч = 1часть. То есть: частота биений равна разности частот этих нот и будет в 2 раза ниже, чем частота нижней Ля и в 3 раза ниже, чем частота верхней Ми. При этом собственно частота этих биений может меняться в зависимости от октавы, в которой мы берем интервал (места в звуковом диапазоне), но соотношения трех этих частот всегда будут оставаться одинаковыми.
Тех, кому не ясно, я снова отсылаю к первой главе книги И. Бентова «Мир как маятник». Соотношения цветов. Так что же такое цвет? Из курса физики нам известно, что свет - это электромагнитное излучение, обладающее волновыми свойствами и некоторыми свойствами частиц. Нас сейчас интересуют только волновые свойства. Чистый белый свет – это спектр, то есть набор излучений всех цветов радуги примерно в одинаковом соотношении. Если есть волновые свойства, значит должна быть у каждого цвета своя частота. Она и есть, только определяют цвета для удобства по обратной величине – длине волны, поскольку частота очень и очень высокая. Попробуем посчитать: если длина волны какого-нибудь зеленого цвета в районе 500 нанометров, то есть 0,5 * 10 - 6м, а скорость света 3 * 10 8м /сек, у нас выйдет частота 6 * 1014 герц, то есть шестьсот террагерц.
Интересно, и как это наш глаз легко отличает зеленый цвет от стоящего в спектре совсем рядом с ним (и отличающегося от него по длине волны всего в несколько процентов) зелено-голубого? Любому человеку, имеющему представление об измерительных приборах, ясно, что расстояние между измеряющими элементами в сетчатке глаза должно быть еще на порядок меньше, то есть примерно 0,05 микрон. Не знаю, - не специалист, но думаю, - так оно и есть, правда, возможно природа создала какой-нибудь новый принцип измерения?
Не будем забывать также, что разделение спектра белого цвета на семь цветов радуги так же условно, как и разделение диапазона звуковой октавы на двенадцать полутонов, - все это для удобства обращения с ними и разговоров о них. На самом деле разделение может быть теоретически бесконечным, и в результате количество цветов и разных новых нот будет так же бесконечно.
И так, - если запоминание стереотипов соотношений развивается от простого к сложному, то можно предположить, что при последующих встречах со знакомыми соотношениями в каком-то процессе нашему мозгу они уже «не интересны», и он пытается выявить новые, - более сложные. Но, исходя из того же, при следующей встрече с этим же процессом мозг наш, опираясь на уже известные соотношения, может выявить и запомнить (принять в обращение) не на много более сложные соотношения. То есть наша гармоническая память может развиваться только поступательно (хотя это еще вопрос, и возможно еще и параллельное развитие), а когда на наш суд выпадает процесс, с куда более сложным соотношением элементов, наш мозг просто перегружается и ничего не записывает в «свою копилку».
Это легко можно проиллюстрировать на нашем отношении к музыке. С одной стороны: нам не интересны и даже раздражают попсовые «два прихлопа – три притопа», с другой стороны: при прослушивании какого-нибудь неизвестного и сложного классического произведения мы быстро устаем, звучащее произведение нам представляется музыкальным хаосом, и становится так же не интересно.
Происходит это потому, что в первом случае наш мозг не находит ничего нового, или даже близко стоящего к верхушке своего гармонического восприятия; во втором же случае наоборот, - наш мозг, опираясь на это же восприятие, не может найти близких по сложности стереотипов соотношений в музыкальном произведении.
Из всего вышесказанного можно сделать еще один вывод: не смотря на то, что все абсолютно люди обладают разным вкусом, тем не менее, иногда (и довольно часто) они готовы понять и искренне согласиться друг с другом, или даже одновременно понять что-то новое на новом более сложном уровне восприятия. Происходит это с людьми, обладающими мощным фундаментом гармонического восприятия, а именно: большим багажом, накопленным в подсознании, - интегрированной суммы знакомых соотношений, и именно потому, что принцип гармонического роста у всех один и тот же, и только условия разные.
Обусловлен, - когда в процессе прослушивания или рассматривания произведения, к уже имеющемуся в памяти пониманию гармонии прибавляется частичка нового знания, то есть подсознательное понимание нового гармонического сочетания. Вообще говоря, идеальной средой для скорейшего гармонического развития является общение с правильно подобранными по возрастанию сложности произведениями искусств, да и, вообще со средой обитания, - всех видимых, слышимых воспринимаемых нами образов. Тут уже главную роль играет мастерство методиста и преподавателя. Только нельзя забывать об изначальном «багаже» обучаемого, свойствах его памяти и наиболее эффективных методах запоминания им гармонических соотношений. Эти свойства у каждого ученика немного разнятся, хотя общий принцип един.
Из работ известного в прошлом канадского психотерапевта Пэнфилда известно, что объем притекающей к коре головного мозга информации от рецепторов далеко не равномерно распределен по всему телу. А именно он считал, что примерно треть приходит от лица, примерно треть – от кистей рук и последняя треть – от всего остального тела. И это при том, что исследовались только осязание и кинестетические ощущения. А как же слух и зрение, которое, как говорят, несет 80% информации в мозг - они же еще более важные источники информации для головного мозга, и к тому же у всех людей развиты далеко не одинаково. Отсюда и принято условно делить людей на визуалистов - потенциальных художников, аудиалистов - потенциальных музыкантов и кинестетиков – потенциальных танцоров. Это, конечно же, и надо учитывать, при подготовке курса гармонического обучения каждого отдельно взятого ребенка.
Как мы понимаем красоту? Обязательно прочитать книгу мемуаров Валерия Александровича Гаврилина “Музыка. И не только о ней” о восприятии музыки, о Шостаковиче и о Соловьеве-Седом, об авторах и исполнителях, о вокальном творчестве вообще. Ведущий радиопередачи Борис Эйфман ссылался еще на книгу Белинского (не помню имени автора) “Записки старого сплетника”. В.А.Гаврилин был учеником Г.Свиридова. <
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.30.237 (0.023 с.) |