
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Об’єм тіла. Об’єм тіла обертання
Розглянемо множину Означення. Тіло Нагадаємо, що циліндром називають тіло, обмежене циліндричною поверхнею з образующими, які паралельні деякій осі, двома площинами, перпендикулярними цій осі. Ці площини в перетині з циліндричною поверхнею утворюють плоскі фігури, які називають основами циліндра, а відстань Нехай тіло
Нехай а тому об’єм За умовою, що Цю формулу називають формулою обчислення об’єму за відомою площею плоских перетинів.
Приклад 6.1. Знайти об’єм тіла, обмеженого поверхнею
Розв'язання. Плоский перетин еліпсоїда площиною з півосями Як відомо, площа цього еліпса дорівнює Нехай тепер тіло
Оскільки площа круга дорівнює
де Якщо тіло одержано обертанням навколо осі
Приклад 6.2. Обчислити об’єм тіла обертання фігури, обмеженої еліпсом
Розв'язання. а) оскільки б) в даному випадку Якщо
Приклад 6.3. Розглянемо тіло
Розв'язання. Зрозуміло, що тому що Одержаний результат можна сформулювати наступним чином: об’єм тора дорівнює площі круга Площа поверхні обертання
Передусім зупинимось, що розуміють під цім терміном. Нехай
Проведемо розбиття де Можна довести, що коли Відмітимо, що можна одержати (7.1) і за ослабленою умовою: Приклад 7.1. Знайти площу поверхні еліпсоїда обертання.
Розв'язання. Нехай еліпс
Якщо Приклад 7.2. Обчислити площу тора (див. приклад. 6.3 розділу ІІІ).
Розв'язання. Зрозуміло, що У даному випадку Під знаком інтеграла необмежена функція і зрозуміло, що він не існує в традиційному сенсі. Чи означає це, що тор немає площі? Поки це свідчить лише про те, що вибране параметричне представлення півкола не задовольняє умові Тому Площа поверхні тора дорівнює довжині кола
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.12.172 (0.019 с.) |
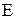 точок простору
точок простору 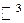 , обмеженою замкненою без перетинів поверхнею. Таку множину
, обмеженою замкненою без перетинів поверхнею. Таку множину 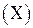 і описані
і описані 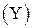 навколо тіла
навколо тіла 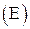 :
: 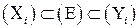 . Символом
. Символом 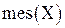 позначають об’єм тіла, через
позначають об’єм тіла, через 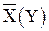 позначимо точну верхню (нижню) грань множини
позначимо точну верхню (нижню) грань множини 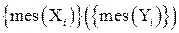 .
.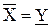 і це число називають об’ємом тіла
і це число називають об’ємом тіла 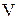 .
.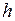 між основами − висотою циліндра.
між основами − висотою циліндра.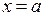 , а справа −
, а справа − 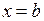 , причому відома площа
, причому відома площа 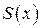 плоскої фігури, яка є перетином тіла
плоскої фігури, яка є перетином тіла 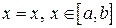 .
.
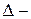 розбиття відрізка
розбиття відрізка 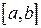 точками
точками 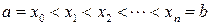 . Проведемо площини
. Проведемо площини 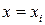 і розглянемо частину
і розглянемо частину 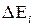 тіла
тіла 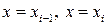 . Довільним чином виберемо
. Довільним чином виберемо 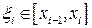 , проведемо площини
, проведемо площини 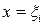 , в перетині з
, в перетині з  . Якщо
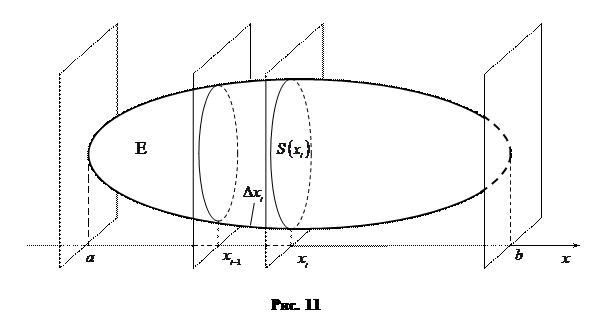
. Якщо 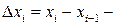 мале, то зрозуміло (рис.11), що
мале, то зрозуміло (рис.11), що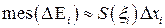 ,
,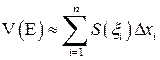
 , можна показати, що
, можна показати, що 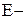 кубіруєме тіло і
кубіруєме тіло і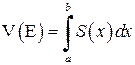 (6.1)
(6.1)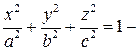 об’єм еліпсоїда.
об’єм еліпсоїда.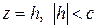 є еліпс
є еліпс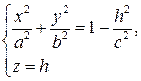
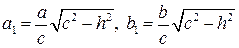 .
.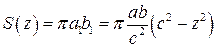 , а тому за формулою (6.1) маємо
, а тому за формулою (6.1) маємо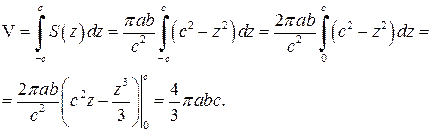
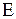 одержане обертанням навколо осі
одержане обертанням навколо осі 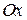 криволінійної трапеції
криволінійної трапеції 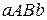 (рис.12). Тоді будь-який переріз перпендикулярний до осі
(рис.12). Тоді будь-який переріз перпендикулярний до осі 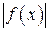 .
.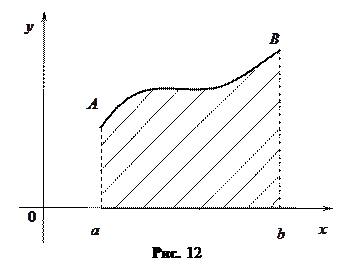
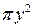 , то за формулою (6.1) маємо
, то за формулою (6.1) маємо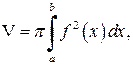 (6.2)
(6.2)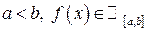 .
. криволінійної трапеції
криволінійної трапеції 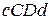 (рис.13), то
(рис.13), то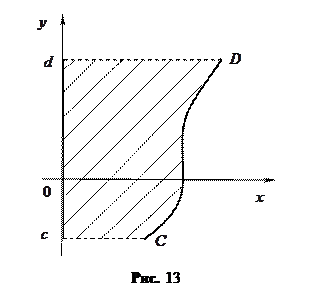
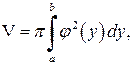 (6.3)
(6.3)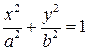 а) навколо осі
а) навколо осі 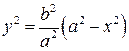 , то за формулою (6.2) маємо
, то за формулою (6.2) маємо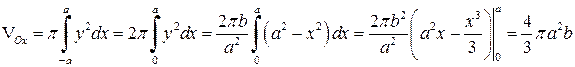
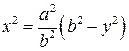 і за формулою (6.3) маємо
і за формулою (6.3) маємо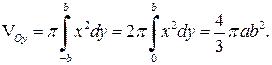
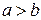 , то зрозуміло, що
, то зрозуміло, що 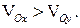
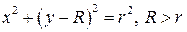 навколо осі
навколо осі 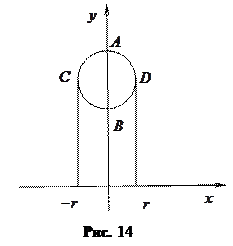
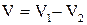 , де
, де 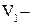 об’єм тіла одержаний обертанням криволінійної трапеції
об’єм тіла одержаний обертанням криволінійної трапеції 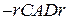 навколо осі
навколо осі 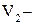 трапеції
трапеції 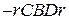 навколо тієї ж осі. За формулою (6.2) і властивістю інтеграла
навколо тієї ж осі. За формулою (6.2) і властивістю інтеграла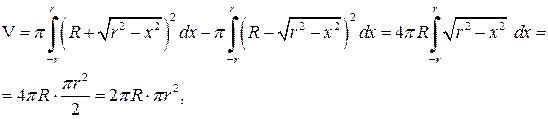
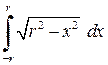 за геометричним змістом визначає площу півкола.
за геометричним змістом визначає площу півкола.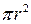 , помноженій на путь
, помноженій на путь 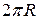 , який пробігає центр ваги при одному обороті навколо осі обертання − відомий як наслідок теореми Гульдіна.
, який пробігає центр ваги при одному обороті навколо осі обертання − відомий як наслідок теореми Гульдіна.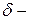 поверхня, одержана обертанням навколо осі
поверхня, одержана обертанням навколо осі 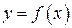 , заданої на відрізку
, заданої на відрізку 
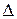 відрізку
відрізку 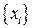 і нехай
і нехай 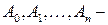 відповідні точки графіка функції
відповідні точки графіка функції 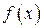 . Побудуємо ломану
. Побудуємо ломану 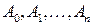 . При обертанні її навколо осі
. При обертанні її навколо осі 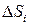 елемента поверхні обертання відповідно
елемента поверхні обертання відповідно 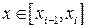 приблизно дорівнює
приблизно дорівнює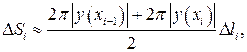
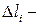 довжина відрізка
довжина відрізка 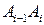 , а значить
, а значить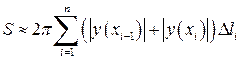 .
.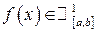 , то поверхня, одержана обертанням кривої
, то поверхня, одержана обертанням кривої 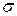 обчислюється за формулою
обчислюється за формулою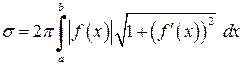 . (7.1)
. (7.1)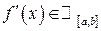 .
.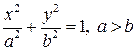 обертається навколо осі
обертається навколо осі 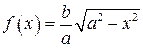 , ексцентриситет
, ексцентриситет 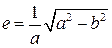 і за формулою (7.1) маємо
і за формулою (7.1) маємо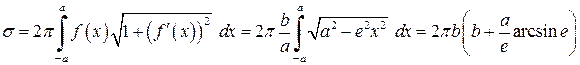 .
.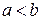 , то, як неважко перевірити,
, то, як неважко перевірити, 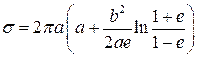 .
.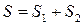 , де
, де 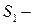 площа поверхні яка одержана обертанням графіка функції
площа поверхні яка одержана обертанням графіка функції 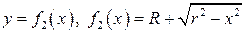 , а
, а 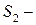 площа поверхні яка одержана обертанням графіка функції
площа поверхні яка одержана обертанням графіка функції 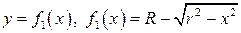 ,
, 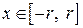 , навколо осі
, навколо осі 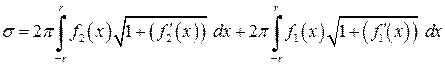 .
.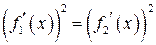 ,
, 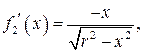
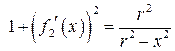 і
і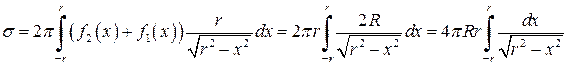 .
.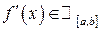 . Поставлена задача потребує розширення поняття інтеграла Рімана і про це ми поговоримо в темі — невласні інтеграли. А щоб завершити розв’язок задачі використаємо параметричне рівняння півкола
. Поставлена задача потребує розширення поняття інтеграла Рімана і про це ми поговоримо в темі — невласні інтеграли. А щоб завершити розв’язок задачі використаємо параметричне рівняння півкола 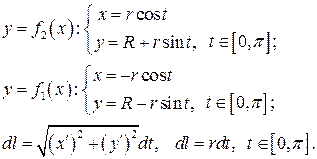
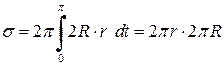 .
.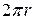 помноженій на путь
помноженій на путь 


