
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление площадей фигур, ограниченных параметрически заданными линиями.Содержание книги
Поиск на нашем сайте
Рассмотрим ситуацию, когда функция
Рис.10 Если криволинейная трапеция ограничена кривой заданной параметрически
,где
Действительно, сделав подставку
Пример 5.3. Найти площадь фигуры, ограниченной одной аркой циклоиды, уравнение которой заданой параметрически Решение.
Для построения фигуры, заданной параметрически, составим таблицу значений координат Нанесем точки
Рис. 10 Согласно формуле (5.5) получим:
=
Таким образом, площадь одной арки циклоиды равна:
По сути, мы вывели формулу для нахождения площади одной арки циклоиды в общем виде. И если на практике вам встретится задача с конкретным значением параметра
Замечание: В некоторых случаях, при нахождении площади фигуры,ограниченной функцией
Пример 5. 4. Найти площадь фигуры, ограниченной эллипсом Решение. Перейдём к параметрическому заданию эллипса где Действительно, если составить таблицу значений координат
Нанести точки
Рис. 11
Учитывая симметрию фигуры относительно координатных осей, найдем площадь четвертой части эллипса
Таким образом, площадь всей фигуры равна:
Вычисление площадей фигур заданных в полярной системе координат. Для нахождения площадей ограниченных кривыми заданных в полярной системе координат нам пригодятся навыки построения графиков функций в данной системе координат, поэтому необходимо вспомнить, что же такое полярная система координат. Полярная система координат и криволинейный сектор. Любая точка в полярной системе координат определятся с помощью полярных координат
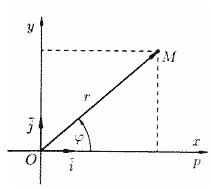
Рис. 12 Формулы перехода от декартовой системы координат к полярной системе координат: Рассмотрим некоторую функцию
В полярной системе может быть задан криволинейный сектор или сегмент.
Криволинейный сектор – это фигура, ограниченная лучами
Площадь криволинейного сектора может быть найдена по формуле
Сегмент- это фигура, ограниченная кривыми
лучами Площадь сегмента может быть найдена по формуле
Пример 5.5. Найти площадь фигуры, ограниченной кривой Решение. Известно, что уравнение
Площадь полученного сектора находим по формуле (5.6):
Замечание: Если в условии не указан диапазон значений угла, то либо этот диапазон совпадает с областью допустимых значений функции Пример 5.6. Найти площадь фигуры, ограниченной кардиоидой Решение. Поскольку
Оставшуюся половину
Рис. 17 Поскольку фигура симметрична относительно оси
Таким образом,
Пример 5.7. Найти площадь фигуры, ограниченной линиями Решение. Посмотрим как это выглядят заданные линии
Получили окружности с центром в начале координат и радиусами 1,3 соответственно. Построим данные линии, учитывая, что угол изменяется от
5.2. Вычисление длины дуги плоской кривой Помимо нахождения площади, определённый интеграл позволяет рассчитать и другие показатели, в частности длину дуги кривой, то есть числовую характеристика протяжённости этой кривой. Длиной дуги кривой линии называют предел, к которому стремится длина вписанной в нее ломаной линии при неограниченном увеличении числа ее звеньев, при этом длина наибольшего звена стремиться к нулю.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.127.14 (0.01 с.) |

 задана в параметрическом виде
задана в параметрическом виде 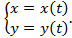
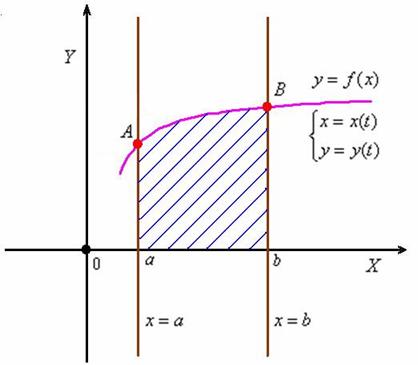
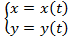 ,
, 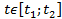 , прямыми
, прямыми  и осью
и осью 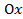 , то её площадь вычисляется по формуле
, то её площадь вычисляется по формуле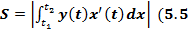 )
)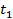 и
и 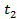 определяются из равенств
определяются из равенств  и
и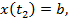 при некотором вполне конкретном значении параметра
при некотором вполне конкретном значении параметра  параметрические уравнения будут определять координаты точки A, а при другом значении
параметрические уравнения будут определять координаты точки A, а при другом значении 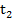 координаты точки B.
координаты точки B.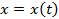 и
и 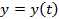 в формуле (5.3),учитывая, что
в формуле (5.3),учитывая, что 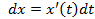 ,
, 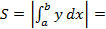
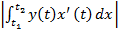 .
.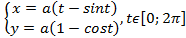 .
.

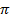

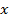
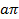
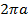
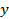
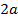
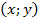 точек кривой, соответствующих различным значениям параметра
точек кривой, соответствующих различным значениям параметра 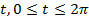 .
.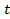 изменяется от 0 до
изменяется от 0 до 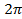 , соответствующая точка
, соответствующая точка 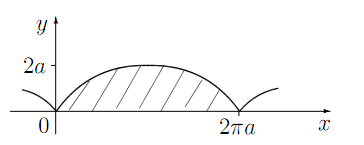
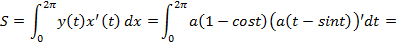
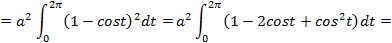
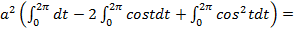
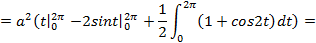
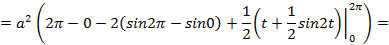

 .
.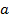 , то вы легко сможете выполнить проверку. Так например при
, то вы легко сможете выполнить проверку. Так например при  ,
, 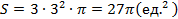
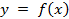 заданной в декартовой системе координат, удобно переходить к параметрическому заданию данной линии,то есть, представить функциональную зависимость через параметр
заданной в декартовой системе координат, удобно переходить к параметрическому заданию данной линии,то есть, представить функциональную зависимость через параметр 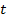 (все эти функции хорошо изучены).Например, при вычислении площади эллипса заданного уравнением
(все эти функции хорошо изучены).Например, при вычислении площади эллипса заданного уравнением 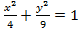 , разрешая уравнение относительно
, разрешая уравнение относительно 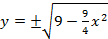 ,
, 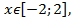 вычисление интеграла от данной функции довольно громоздко, поэтому целесообразно перейти к параметрическому заданиюэллипса.
вычисление интеграла от данной функции довольно громоздко, поэтому целесообразно перейти к параметрическому заданиюэллипса.
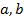 полуоси эллипса, в нашем случае
полуоси эллипса, в нашем случае 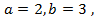 следовательно исходное уравнение в параметрическое форме имеет вид
следовательно исходное уравнение в параметрическое форме имеет вид 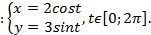

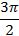
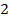
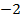
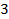
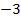
 (рис.11).
(рис.11).
 ,здесь
,здесь  до 0. Согласно формуле (5.5) получим:
до 0. Согласно формуле (5.5) получим:

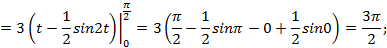
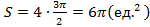 .
.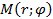 , где
, где  – расстояние от начала координат
– расстояние от начала координат  (полюса) до точки
(полюса) до точки 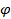 – угол между положительным направлением действительной оси
– угол между положительным направлением действительной оси 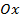 и(движемся против часовой стрелки) радиус-вектором
и(движемся против часовой стрелки) радиус-вектором  точки
точки 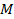 (рис. 12).
(рис. 12).
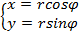 ,
, 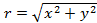 ;
;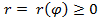 заданную в полярной системе координат принимающую неотрицательные значения на отрезке
заданную в полярной системе координат принимающую неотрицательные значения на отрезке 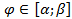 , где
, где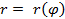 - длина радиус – вектора, соединяющего полюс O с произвольной точкой кривой
- длина радиус – вектора, соединяющего полюс O с произвольной точкой кривой 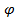 - угол наклона этого радиус – вектора к полярной оси Op.
- угол наклона этого радиус – вектора к полярной оси Op.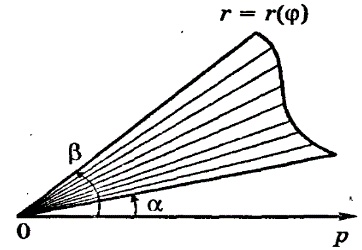
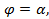
 и некоторой линией
и некоторой линией  (рис. 13).
(рис. 13).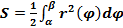 (5. 6)
(5. 6)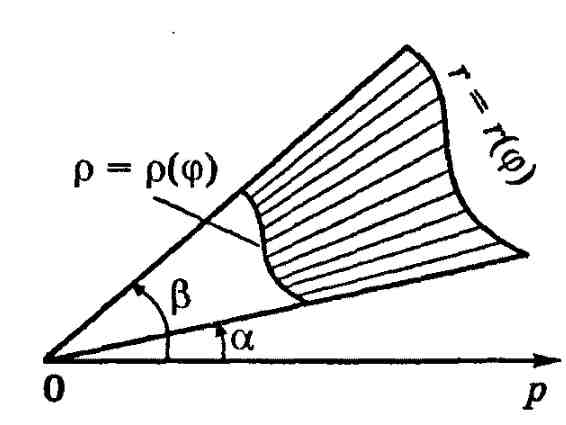
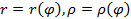 и
и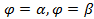 (рис.14).
(рис.14).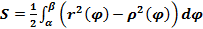 (5. 7)
(5. 7) .
.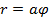 задает кривую в полярных координатах, которая называется спиралью Архимеда. В нашем случае
задает кривую в полярных координатах, которая называется спиралью Архимеда. В нашем случае 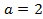 , изобразим фигуру- отметим полюс, изобразим полярную ось Ор, начертим угловые направления
, изобразим фигуру- отметим полюс, изобразим полярную ось Ор, начертим угловые направления 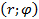 и соединим их линией (рис. 16):
и соединим их линией (рис. 16):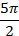
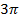

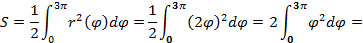
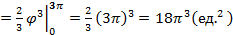 .
. ,либо принимается равным отрезку
,либо принимается равным отрезку  .
.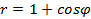 .
. чётная функция,действительно,
чётная функция,действительно, 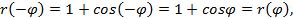 а как известно, четная функция симметрична относительно оси
а как известно, четная функция симметрична относительно оси 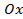 ,поэтому достаточно построить половину фигуры на промежутке
,поэтому достаточно построить половину фигуры на промежутке 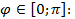

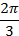

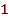

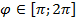 отображаем симметрично относительно оси
отображаем симметрично относительно оси 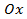 (рис.17)
(рис.17)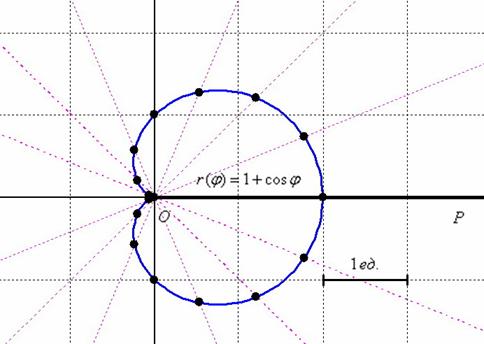
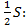
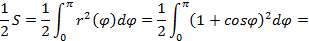
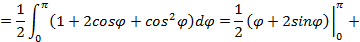
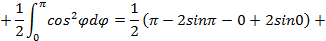
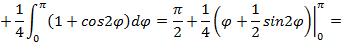
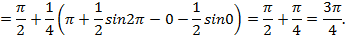
 .
.
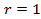 ,
, 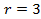 ,
, 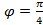 ,
, 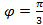 .
.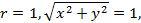
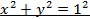 ;
; 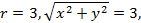
 .
. 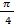 до
до 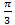 (рис.18), получили сегмент, его площадь находим по формуле (5.7):
(рис.18), получили сегмент, его площадь находим по формуле (5.7):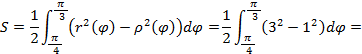
 .
.


