Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практическая работа № 22. «Определение общих свойств функций».Содержание книги
Поиск на нашем сайте
Цель работы: Определение общих свойств функций Требования к теоретической готовности обучающегося к выполнению практической работы: Для выполнения практической работы обучающийся должен: уметь: - определять область определения функций - определять чётность и монотонность функций Знать: - определение функции и способы их задания - определения общих свойств функций Задания практической работы. 1. Определите чётность функций: а) у = 2. Достройте график функции, если она: а) чётная б) нечётная.
3. Найдите область определения функции: А) у = е) 4. Определите монотонность функции: а) у = 5 – 2х б) у = 5. Определите чётность функций: а) в) 6. Достройте график функции, если она: а) чётная б) нечётная.
7. Найдите область определения функции: а) в) 8. Определите монотонность функции: а) 9. Не выполняя построения графика функции y=1,2x-7 выясните, проходит ли этот график через точку: а) А(100;113); б) В (-15;-25). 10. Функция f – убывающая. Сравните: а) f(-2) и f(2). б) f(3) и f(5) в) f (4) и f(2) 11. Функция g – возрастающая. Сравните: а) g(-2) g(2) б) g(3) и g(5) в) g(4) и g(2)
Информационные материалы для выполнения заданий. Функция – зависимость у от переменной х, при которой каждому значению х соответствует единственное значение у. Х – независимая переменная (аргумент), у – зависимая переменная (функция).
А) функция возрастает, если Б) функция убывает, если
(y > 0), и отрицательна (y < 0). Образцы решения типовых задач Пример 1. Определите чётность функции: а) Функция нечётная, так изменился знак. б) функция чётная, так как все знаки сохранились. Пример 2. Найдите область определения функции: а) б) в) Пример 3. Не выполняя построения графика, определите монотонность функции
А)
Т.к 0 < 1
Б) Т.к 0 < 1 Критерии оценивания
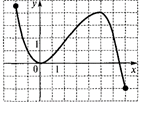
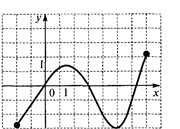
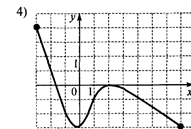
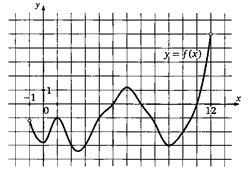
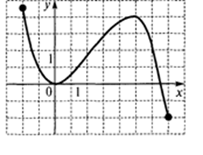
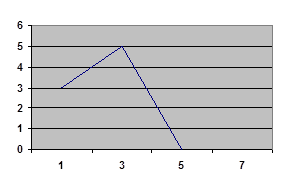
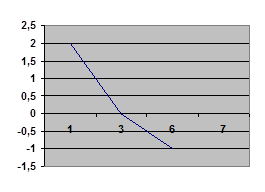
Практическая работа № 23. «Построение и чтение графиков». Цель работы: Применение свойств функций для построения и чтения графиков. Требования к теоретической готовности обучающегося к выполнению практической работы: Для выполнения практической работы обучающийся должен: уметь: - определять свойства функций по графику знать: - определения общих свойств функций Выполните задания и оформите решение в тетрадях 1. Перечислите свойства функций, изображённых на рисунке: а) б) в)
2. На графике показано суточное количество осадков, выпавших с 1 по 11 февраля. По горизонтали указываются числа месяца, по вертикали — количество осадков в мм, выпавшее в соответствующий день. Определите по графику наибольшее количество осадков, выпавших за день в этот период.
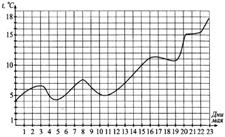
3. На рисунке показано изменение температуры воздуха с 1 по 23 мая. По горизонтали отмечены числа месяца, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку, какого числа в период с 3 по 12 мая температура достигла наибольшего значения.
4. Постройте график функции f, если известны её свойства: · Область определения: [- 6; 6], область значений: [- 2; 5] · Точки пересечения графика с осью Ох: А (-4; 0), В (-2; 0) · Точки пересечения графика с осью Оу: С (0; 2,5) ·.Промежутки знакопостоянства f (х) > 0: [-6; -4), (-2; 6]; f (х) < 0: (-4; -2) · Промежутки возрастания: [-3; 1], [4; 6]; убывания: [-6; -3], [1; 4] · xmax = 1, f (1) = 3; xmin = - 3, f (-3) = - 2; xmin = 4, f (4) =1 · Дополнительные точки графика f (-6) = 3, f (6) = 5 5. Постройте график функции: у = х2 – 4х + 1. 6. Перечислите свойства функции по графику: А) Б)
В)
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.166.157 (0.007 с.) |

 б) у =
б) у = 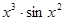 в) у =
в) у = 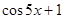 г) у =
г) у =  д) у =
д) у = 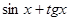
 б) у =
б) у = 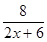 в)
в)  г)
г) 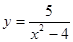 д)
д) 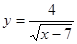

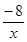
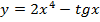 б)
б) 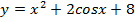
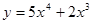 г)
г) 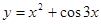 д)
д) 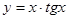 е)
е) 

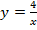 б)
б) 
 Г)
Г) 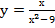 д)
д) 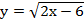 е)
е) 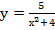
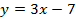 .
.
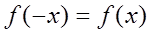

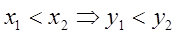

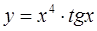 Решение:
Решение: 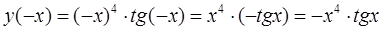 ,
, . Решение:
. Решение: 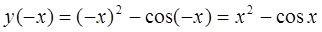 ,
,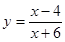 . Решение: Д(у):
. Решение: Д(у): 
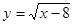 . Решение: Д(у):
. Решение: Д(у): 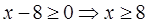
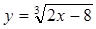 . Решение: Д(у): х – любые числа, т. е R
. Решение: Д(у): х – любые числа, т. е R . Решение:
. Решение: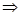 8 > 6, то функция убывающая.
8 > 6, то функция убывающая.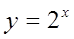 . Решение:
. Решение: