Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составление таблицы истинностиСодержание книги Поиск на нашем сайте
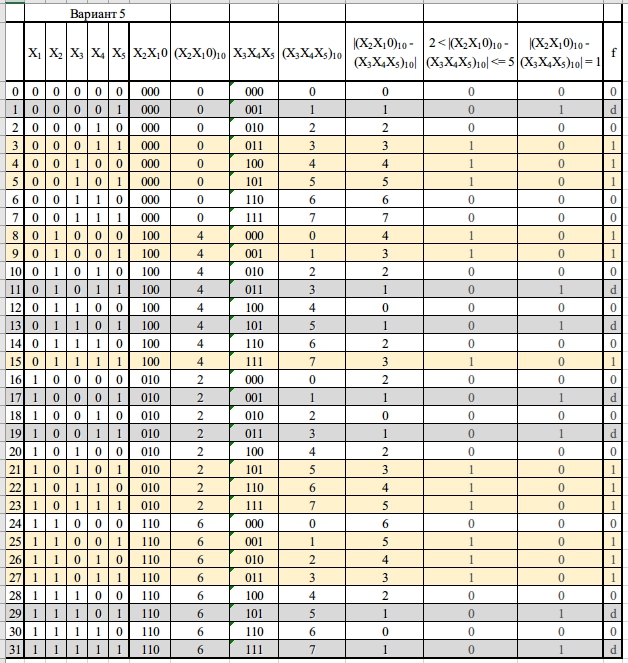
Таблица истинности для функции от 5ти переменных X1, X2, X3, X4, X5 заданная выражением 2 < |(X2X10)10 - (X3X4X5)10| <= 5 и имеющим неопределенное значение при условии: |(X2X10)10 - (X3X4X5)10| = 1 (Таблица 1)
ПРЕДСТАВЛЕНИЕ БУЛЕВОЙ ФУНКЦИИ В АНАЛИТИЧЕСКОМ ВИДЕ С ПОМОЩЬЮ КДНФ И ККНФ Запишем булеву функцию в канонических ДНФ и КНФ. d состояния для уменьшения числа термов при КНДФ заменяем на ноль, а при ККНФ на единицу. КДНФ: f = ККНФ: f = (X1 ˅ X2 ˅ X3 ˅ X4 ˅ X5 ) (X1 ˅ X2 ˅ X3 ˅
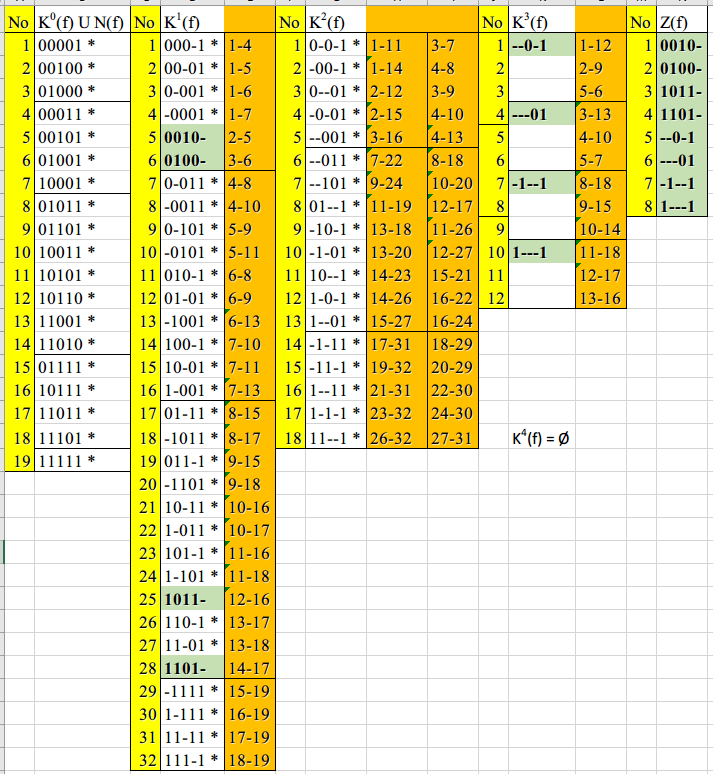
МИНИМИЗАЦИЯ БУЛЕВОЙ ФУНКЦИИ МЕТОД КВАЙНА – МАК-КЛАСКИ Чтобы получить сокращенную ДНФ булевой функции из ее совершенной ДНФ по теореме Квайна, надо выполнить всевозможные неполные склеивания соседних конъюнкций, а затем всевозможные поглощения конъюнкций. Мак Класки сформулировал алгоритм, который организует построение сокращенной ДНФ более эффективно, чем это предложено в теореме. Для использования метода Квайна-Мак-Класки для начала необходима таблица истинности для 0-куба. Для достижения максимального r-куба d в исходной таблице истинности заменяется на 1.
Таблица 2 Простые импликанты Используя таблицу простых импликантов и проводя операцию склейки, находятся кубы максимальной размерности. Термы, которые не участвовали в операции склейки, отмечены зеленым (простые импликанты) и составляют покрытие Z(f) (Таблица 2). Оно задает СДНФ исходной функции. Склеиваемые термы отмечены *, справа от полученного терма написаны номера, из которых они получились.
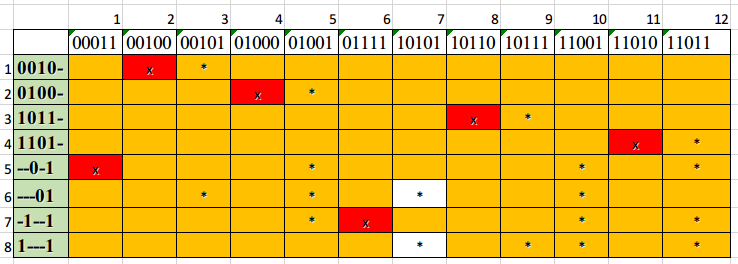
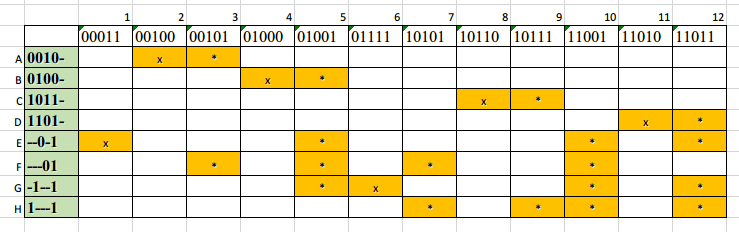
Таблица 3 Импликантная таблица Чтобы отобразить покрытие простыми импликантами существенных вершин составляется имплекантная таблица. Каждая строка это простая импликанта, а каждый столбец – один из 0-кубов (Таблица 3). Для неполностью определенной функции безразличные наборы исключаются. Далее выделяем множество существенных импликант. Находятся столбцы с одной меткой (выделены красным х). Строки соответствующих импликант удаляются (закрашиваются оранжевым), захватавая другие отмеченные * столбцы, которые встречаются в удаляемой строке. Множество всех существенных импликант (строки с красным х, 1-5, 7) образует ядро покрытия Т. T = {0010-; 0100-; 1011-; 1101-; --0-1; -1--1} Термы ядра: Удалив ядро из таблицы получим упрощенную импликантную таблицу (Таблица 4).
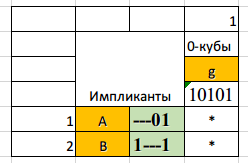
Таблица 4 Упрощенная импликантная таблица Термы упрощенной таблицы (выбираем любой, оба покрывают g 0-куб) и добавляем его к ядру покрытия, чтобы получить минимальное покрытие: Сmin = {0010-; 0100-; 1011-; 1101-; --0-1; -1--1; 1---1} 1---1 соответствует X1X5, следовательно МДНФ: f = Вычислим цену покрытия Sa, которая является количеством переменных, участвующих в записи МДНФ; цену покрытия Sb, которая является суммой цены Sa и количества термов МДНФ. Данные цены образуют предельные границы цены схемы по Квайну: Sa ≤ SQ ≤ Sb. Посчитаем цену покрытия: Sa = 22, Sb = 29 Неравенство ограничения цены схемы по Квайну: 22 ≤ SQ ≤ 29.
МЕТОД ПЕТРИКА Невозможно применить к упрощенной таблице из-за ее маленького объема, поэтому применяем к обычной таблице.
Таблица 5 Таблица для метода Петрика Для метода Петрика нужно выписать булево выражение Y, покрывающее все существенные вершины: Y = EA(A ˅ F)B(B ˅ E ˅ F ˅ G)G(F ˅ H)C(C ˅ H) (E ˅ F ˅ G ˅ H)D(D ˅ E ˅ G ˅ H) Попарно умножив термы с одинаковыми буквами, применив закон поглощения, упростим выражение и приведем его к дизъюнктивной форме: Y = ABCDEG(F v H) = ABCDEGF v ABCDEGH Оба терма состоят из 7ми букв, так что можно выбрать любой. ABCDEGH соответствует минимальному покрытию: Сmin = {0010-; 0100-; 1011-; 1101-; --0-1; -1--1; 1---1} МДНФ ( также не изменилась): f = Цена не изменилась: Sa = 22, Sb = 29 Цена по методу Квайна – Мак – Класки не изменилась в методе Петрика, потому что в итоге выбирается одинаковое количество импликант с одинаковым покрытием вершин. Метод Квайна – Мак – Класки скорее визуальный, а метод Петрика позволяет точно вычислить каждую комбинацию импликантов и покрытых вершин, где потом выбирается вариант с минимальным покрытием.
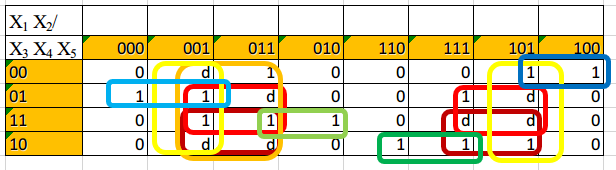
МЕТОД КАРТ КАРНО ДЛЯ МДНФ Для определения МДНФ функции рассмотрим карты с единичными значениями функции, а также доопределим значение d до единицы (Таблица 6). Выделяем области с максимальным количеством единиц, которые могут содержать количество элементов кратное двум в степени n, те. 2, 4, 8..
Таблица 6 Карты Карно при МДНФ
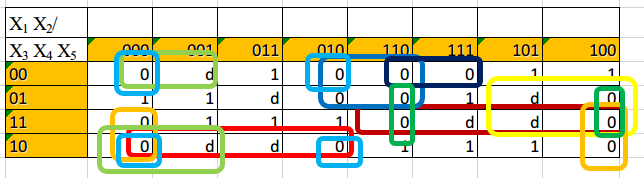
ДЛЯ МКНФ Для определения МКНФ функции рассмотрим карты с нулевыми значениями функции, а также доопределим значение d до нуля (Таблица 7). Выделяем области с максимальным количеством нулей, которые могут содержать количество элементов кратное двум в степени n, те. 2, 4, 8..
Таблица 7 Карты Карно при МКНФ
Посчитаем цену покрытия: Sa = 28, Sb = 37 Неравенство ограничения цены схемы по Квайну: 28 ≤ SQ ≤ 37.
Сравним цены различных МДНФ и МКНФ. Границы для МДНФ: Ограничения цены схемы по Квайну, метод К-М-К: 22 ≤ SQ ≤ 29. Ограничения цены схемы по Квайну, метод Петрика: 22 ≤ SQ ≤ 29 Ограничения цены схемы по Квайну, метод карт Карно: 24 ≤ SQ ≤ 32 Границы для МКНФ: Ограничения цены схемы по Квайну, метод карт Карно: 28 ≤ SQ ≤ 37 Для факторизации и декомпозиции берем МДНФ, полученную методом К-М-К и методом карт Карно, потому что они имеют наименьшую Sa, равную 22 и 24.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 1070; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.132.80 (0.006 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 1
1 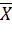 1
1